Batch Norm 拟合进神经网络(Fitting Batch Norm into a neural network)
你已经看到那些等式,它可以在单一隐藏层进行Batch归一化,接下来,让我们看看它是怎样在深度网络训练中拟合的吧。
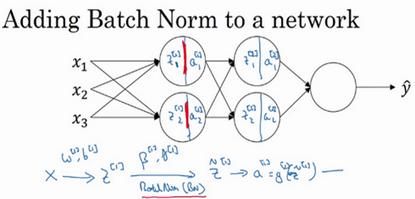
假设你有一个这样的神经网络,我之前说过,你可以认为每个单元负责计算两件事。
第一,它先计算z,然后应用其到激活函数中再计算a,所以我可以认为,每个圆圈代表着两步的计算过程。
同样的,对于下一层而言,那就是z_1^([2])和a_1^([2])等。
所以如果你没有应用Batch归一化,你会把输入X拟合到第一隐藏层,然后首先计算z^([1]),这是由w^([1])和b^([1])两个参数控制的。
接着,通常而言,你会把z^([1])拟合到激活函数以计算a^([1])。
但Batch归一化的做法是将z^([1])值进行Batch归一化,简称BN,此过程将由β^([1])和γ^([1])两参数控制,这一操作会给你一个新的规范化的z^([1])值(̃z^([1])),然后将其输入激活函数中得到a^([1]),即a^([1])=g^([1]) (̃z^([l]))。
现在,你已在第一层进行了计算,此时Batch归一化发生在z的计算和a之间,接下来,你需要应用a^([1])值来计算z^([2]),此过程是由w^([2])和b^([2])控制的。
与你在第一层所做的类似,你会将z^([2])进行Batch归一化,现在我们简称BN,这是由下一层的Batch归一化参数所管制的,即β^([2])和γ^([2]),现在你得到̃z^([2]),再通过激活函数计算出a^([2])等等。
所以需要强调的是Batch归一化是发生在计算z和a之间的。
直觉就是,与其应用没有归一化的z值,不如用归一过的̃z,这是第一层(̃z^([1]))。
第二层同理,与其应用没有规范过的z^([2])值,不如用经过方差和均值归一后的̃z^([2])。
所以,你网络的参数就会是w^([1]),b^([1]),w^([2])和b^([2])等等,我们将要去掉这些参数。但现在,想象参数w^([1]),b^([1])到w^([l]),b^([l]),我们将另一些参数加入到此新网络中β^([1]),β^([2]),γ^([1]),γ^([2])等等。
对于应用Batch归一化的每一层而言。需要澄清的是,请注意,这里的这些β(β^([1]),β^([2])等等)和超参数β没有任何关系,后面会解释原因,后者是用于Momentum或计算各个指数的加权平均值。
Adam论文的作者,在论文里用β代表超参数。Batch归一化论文的作者,则使用β代表此参数(β^([1]),β^([2])等等),但这是两个完全不同的β。我在两种情况下都决定使用β,以便你阅读那些原创的论文,但Batch归一化学习参数β^([1]),β^[2] 等等和用于Momentum、Adam、RMSprop算法中的β不同。
所以现在,这是你算法的新参数,接下来你可以使用想用的任何一种优化算法,比如使用梯度下降法来执行它。
举个例子,对于给定层,你会计算dβ^([l]),接着更新参数β为β^([l])=β^([l])-αdβ^([l])。你也可以使用Adam或RMSprop或Momentum,以更新参数β和γ,并不是只应用梯度下降法。
即使在之前的笔记中,已经解释过Batch归一化是怎么操作的,计算均值和方差,减去均值,再除以方差,如果它们使用的是深度学习编程框架,通常你不必自己把Batch归一化步骤应用于Batch归一化层。
因此,探究框架,可写成一行代码,比如说,在TensorFlow框架中,你可以用这个函数(tf.nn.batch_normalization)来实现Batch归一化,我们稍后讲解,但实践中,你不必自己操作所有这些具体的细节,但知道它是如何作用的,你可以更好的理解代码的作用。但在深度学习框架中,Batch归一化的过程,经常是类似一行代码的东西。(这些框架是个好东西,要知道里面咋么用的,其实就很简单了,这里是概念培养)
所以,到目前为止,我们已经讲了Batch归一化,就像你在整个训练站点上训练一样,或就像你正在使用Batch梯度下降法。
实践中,Batch归一化通常和训练集的mini-batch一起使用。
你应用Batch归一化的方式就是,你用第一个mini-batch(X^({1})),然后计算z^([1]),这和上张幻灯片上我们所做的一样,应用参数w^([1])和b^([1]),使用这个mini-batch(X^({1}))。接着,继续第二个mini-batch(X^({2})),接着Batch归一化会减去均值,除以标准差,由β^([1])和γ^([1])重新缩放,这样就得到了̃z^([1]),而所有的这些都是在第一个mini-batch的基础上,你再应用激活函数得到a^([1])。然后用w^([2])和b^([2])计算z^([2]),等等,所以你做的这一切都是为了在第一个mini-batch(X^({1}))上进行一步梯度下降法。
类似的工作,你会在第二个mini-batch(X^{2} )上计算z^([1]),然后用Batch归一化来计算̃z^([1]),所以Batch归一化的此步中,你用第二个mini-batch(X^{2} )中的数据使̃z^([1])归一化,这里的Batch归一化步骤也是如此,让我们来看看在第二个mini-batch(X^{2} )中的例子,在mini-batch上计算z^([1])的均值和方差,重新缩放的β和γ得到z^([1]),等等。
然后在第三个mini-batch(X^{3} )上同样这样做,继续训练。
现在,我想澄清一个参数的一个细节。
先前我说过每层的参数是w^([l])和b^([l]),还有β^([l])和γ^([l]),请注意计算z的方式如下,z^([l])=w^([l]) a^[l-1] +b^([l]),但Batch归一化做的是,它要看这个mini-batch,先将z^([l])归一化,结果为均值0和标准方差,再由β和γ重缩放,但这意味着,无论b^([l])的值是多少,都是要被减去的,因为在Batch归一化的过程中,你要计算z^([l])的均值,再减去平均值,在此例中的mini-batch中增加任何常数,数值都不会改变,因为加上的任何常数都将会被均值减去所抵消。
所以,如果你在使用Batch归一化,其实你可以消除这个参数(b^([l])),或者你也可以,暂时把它设置为0,那么,参数变成z^([l])=w^([l]) a^[l-1] ,然后你计算归一化的z^([l]),̃z^([l])=γ^([l]) z^([l])+β^([l]),你最后会用参数β^([l]),以便决定̃z^([l])的取值,这就是原因。
所以总结一下,因为Batch归一化超过了此层z^([l])的均值,b^([l])这个参数没有意义,所以,你必须去掉它,由β^([l])代替,这是个控制参数,会影响转移或偏置条件。
最后,请记住z^([l])的维数,因为在这个例子中,维数会是(n^([l]),1),b^([l])的尺寸为(n^([l]),1),如果是l层隐藏单元的数量,那β^([l])和γ^([l])的维度也是(n^([l]),1),因为这是你隐藏层的数量,你有n^([l])隐藏单元,所以β^([l])和γ^([l])用来将每个隐藏层的均值和方差缩放为网络想要的值。
让我们总结一下关于如何用Batch归一化来应用梯度下降法,假设你在使用mini-batch梯度下降法,你运行t=1到batch数量的for循环,你会在mini-batch X^{t} 上应用正向prop,每个隐藏层都应用正向prop,用Batch归一化代替z^([l])为̃z^([l])。
接下来,它确保在这个mini-batch中,z值有归一化的均值和方差,归一化均值和方差后是̃z^([l]),然后,你用反向prop计算dw^([l])和db^([l]),及所有l层所有的参数,dβ^([l])和dγ^([l])。尽管严格来说,因为你要去掉b,这部分其实已经去掉了。
最后,你更新这些参数:w^([l])=w^([l])-αdw^([l]),和以前一样,β^([l])=β^([l])-αdβ^([l]),对于γ也是如此γ^([l])=γ^([l])-αdγ^([l])。
如果你已将梯度计算如下,你就可以使用梯度下降法了,这就是我写到这里的,但也适用于有Momentum、RMSprop、Adam的梯度下降法。
与其使用梯度下降法更新mini-batch,你可以使用这些其它算法来更新,我们在之前一些笔记中讨论过的,也可以应用其它的一些优化算法来更新由Batch归一化添加到算法中的β 和γ 参数。
我希望,你能学会如何从头开始应用Batch归一化,如果你想的话。
如果你使用深度学习编程框架之一,我们之后会谈。希望你可以直接调用别人的编程框架,这会使Batch归一化的使用变得很容易(其实学会了之后,一般都是这么用的,没有人会自己去推导着写)。
现在,以防Batch归一化仍然看起来有些神秘,尤其是你还不清楚为什么其能如此显著的加速训练,我们进入下一个笔记,详细讨论Batch归一化为何效果如此显著,它到底在做什么。