前一章介绍了线性回归有很多强大的方法,但是缺点是创建的模型需要拟合所有的样本点(局部加权线性回归除外),当数据拥有很多特征并且特征之间关系复杂那就很麻烦了,况且生活中很多问题不是线性的,无法用线性模型拟合出来。
本章介绍CART(分类回归树),该算法既可以用于分类又可以用于回归。回归树是在每个叶节点上使用各自的均值做预测,更高级的模型树是在每个叶节点上都构建出一个线性模型。此外,在回归树中介绍了树剪枝技术,目的是防止树的过拟合。
9.1 复杂数据的局部性建模
第3章使用ID3方法构建树,做法是每次选取当前最佳特征来分割数据,并按照特征所有可能值来切分。这里的方法是二元切分法,即每次把数据集分成两份。根据特征值大小进入左右两个子树。
9.2连续和离散型特征的树的构建
在树的构建过程中,需要解决多种类型数据的存储问题,这里用字典来存储树的数据结构,字典里有四个元素:切分特征,待切分特征值,左子树,右子树。
本章构建两个树:回归树,其每个叶节点包含单个值。模型树,其每个叶节点包含一个线性方程。
9.3将CART用于回归
构建回归树思路:遍历所有特征的所有特征值,对每一个特征值都进行一次数据集的划分,然后算划分后的两个子集总方差之和,找到能使总方差之和最小的划分特征值,然后进行一次划分,得到两个树,对两个树递归进行相同操作。
约束条件:划分的两个数据集必须都大于多少行(如4行),防止划分的一边太大一边太小,如果不满足就不对这个特征值划分。如果划分后两个子集的总方差之和与原总方差相差不大也不划分,直接返回叶节点,表示不能再划分了。如果目标变量都是一样的,那肯定就不用划分了,直接返回叶节点。
总结:划分后叶节点的大小是叶节点数据集目标变量的均值,所以说,上面的做法就是把一团一团的数据分开来,总方差就是分开他们的依据,均值就是各数据集的一种表示。
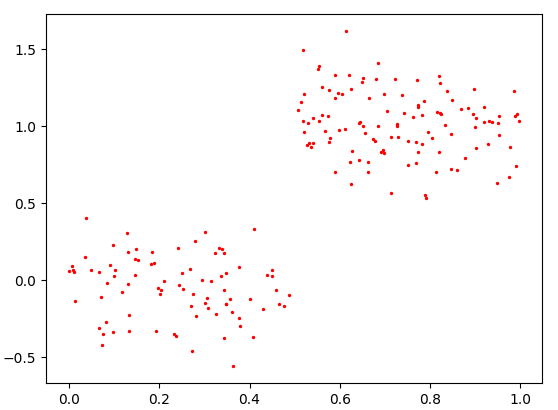
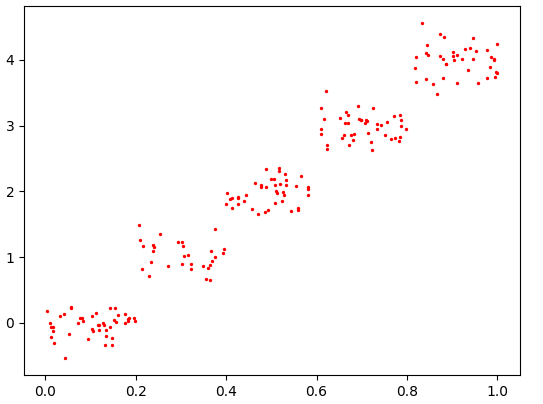
下图是两个示例:
图一图二是不同的数据集画出来的(
这句是废话
)。很明显,图一肯定会被划成2个子集,也就是2个叶节点,图二会被划成5个子集,也就是5个叶节点。如下:
所以,创建回归树有点像把抱团的子数据集划分开,均值是他们各自中心点的体现,总方差是他们之间的远近。
9.4 树剪枝
通过降低决策树的复杂程度来避免过拟合的过程就是剪枝。剪枝可以分为预剪枝和后剪枝。前面提到的约束条件其实就是预剪枝,比如划分的子集少于4行就不划分,还有划分后的总方差之和与原方差相差不大就不划分,说白了就是不要划分的太细,划分太细可不就是过拟合了吗~后剪枝需要使用测试集和训练集。
9.4.1预剪枝
说说预剪枝的缺点,上面的简单实验用到了预剪枝,效果还可以,但是其实是有问题的。因为上面的算法对参数tolS和tolN很敏感。比如tolS=0,表示划分后方差只要有减少就对数据集进行划分。tolN=1,表示划分后两个子集哪怕只有一行也要划分子集,也就是说每个样本都成了一个叶节点。
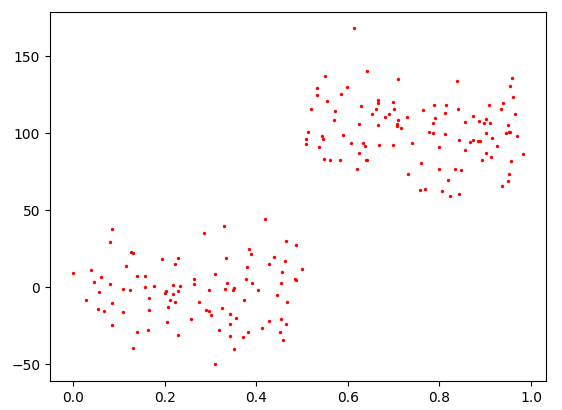
可以看到这个散点图和ex00.txt的散点图相似,但是这个图y轴的数量级是ex00.txt图的100倍,这意味这什么?意味着创建树时对误差的选择很重要,之前的tolS=1完全不行,这样会创建很多叶节点,创建的树十分臃肿,当tolS=10000时才会得到只有两个叶节点的树。
所以,通过不断修改停止条件来得到合理的结果并不是一个很好的做法,况且很多时候我们也不知道我们想要的结果是什么。而这正是机器学习需要做的:给出数据的总体样貌。
9.4.2 后剪枝
使用后剪枝方法需要将数据集分成测试集和训练集。首先指定参数,使构建的树足够大,足够复杂,便于剪枝。接下来从上而下找到叶节点,用测试集来判断将这些叶节点合并能否降低测试误差,如果能就合并。
代码运行结果就不放了,巨多,放了也没有什么直观的可比性。代码思路:先用训练数据训练出一棵树,然后用训练好的树和测试数据作为输入进行自上而下的递归剪枝。
过程:首先测试数据集根据训练好的树来划分子集,然后剪枝。递归到最后,就是比较最底层两个叶节点合并后的总方差和不合并的各自总方差之和哪个更大,如果合并了方差变小了就剪枝,而剪枝就是把两个叶节点的数值相加除以2,表示两个子集合并,均值就是两个子集均值的平均值。(书中说是自上而下剪枝,但其实是自下而上合并,最后合并到不需要合并结束,最后遍历完整个测试数据集。它所说的自上而下估计是因为递归是自上而下,也有可能是我算法没学好,不理解这四个字的含义(@_@))
最后,结果是大量节点被剪枝掉了,但是没有像预期那样剪成两个部分,这说明后剪枝不如预剪枝有效。一般的, 为了寻求最佳模型可以同时使用两种剪枝技术。
9.5 模型树
模型树比回归树好的地方在于:模型树可解释,有更高的预测准确度。它与回归树的不同在于叶节点不是只用一个数值表示,而是一个线性函数。
模型树和回归树算法的不同点主要有两个:一是叶节点,模型树会将叶节点数据集的回归系数作为叶节点的表示。二是误差,回归树是计算总方差,模型树是计算预测结果与真实结果的平方差。所以创建树的函数以及选择最优划分特征的函数可以通用,只要改变叶节点表达函数和误差计算函数即可。
下面是示例:
很明显exp2.txt用模型树来拟合会有很好的效果,结果如下:
可以看到,建立的模型树以0.285477为界创建了两个模型。两个模型是线性函数,与真实模型十分接近。
9.6 示例:树回归与标准回归的比较
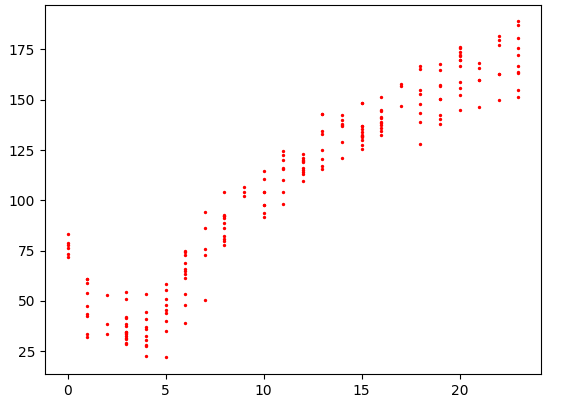
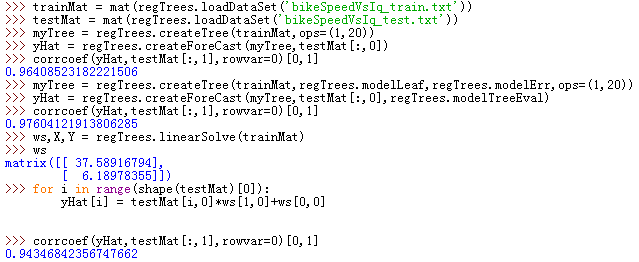
模型树、回归树以及前一章的普通线性回归,哪一种模型更好?有一个客观的方法,就是计算他们预测结果与真实结果的相关系数。本示例就是分别计算三种模型的预测结果并将他们与真实结果的相关系数做一下比较。
用树回归进行预测的代码思路:首先用训练数据训练出一棵树,然后对测试数据进行递归,根据划分特征与测试数据对应特征值大小找到测试数据所在叶节点,然后根据叶节点返回预测值,即为此测试数据的预测值。在回归树中,此预测值就是叶节点数据集目标变量的均值。在模型树中,此预测值就是测试数据与叶节点回归系数乘积得到的预测值。
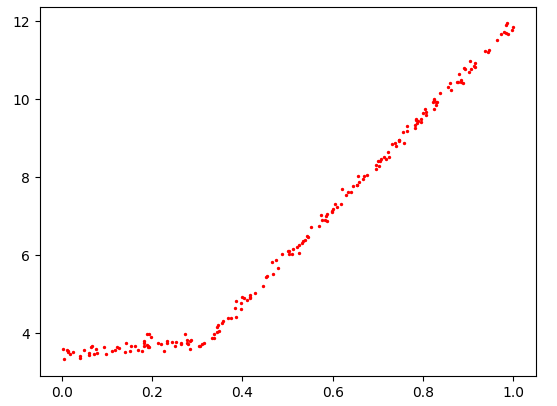
下面给出测试数据的图:
总结:很明显,树回归在预测复杂数据时会比简单的线性模型更有效。而对于这个数据集,模型树方法比回归树方法效果更好一些。个人认为,模型树方法有点像是普通线性回归的变种,或者说是分段的线性回归。对于有这种特征的数据,显然模型树会比回归树表现的更好,因为我感觉回归树更适用于一个个抱团的子数据集组成的大数据集,而每个子数据集都是一个叶节点。
总的来说,回归树更擅长将数据集中一个个抱团的子数据集分开,每个子数据集就是一个叶节点,叶节点通过子数据集目标变量的均值来表达。而模型树更擅长将数据集中一段段线性的子数据集分开,每一段子数据集就是一个叶节点,叶节点用线性回归的方法来表达。
9.7 使用Python的Tkinter库创建GUI
本节内容:
首先介绍如何利用一个现有模块Tkinter来构建GUI
之后介绍如何在Tkinter和绘图库之间交互
最后通过创建GUI使人们能够自己探索模型树和回归树的奥秘。
本章我只是概览了一下,没有详细研究代码,以后有需要再回头研究。主要工作就是用Tkinter创建GUI,然后集成Matplotlib和Tkinter,就可以得到一个图形用户界面,更方便直观地展示数据的分析结果。以下是对数据创建回归树和模型树的两幅图:
PS:费了老鼻子劲才搞出这两张图,中间一直报错也很难找到结果,代码明明就是和书上一毛一样。最终百度了无数,好不容易找到了类似的问题,又从别人一句微不足道的评论里找到了答案,试一试,出来了。真真是谢谢他八辈儿祖宗了~问题出在画点时括号里的数据集参数得是数组,声明一下即可。心累额......
9.8本章小结
在小结中看到一种说法,也是有道理的,即回归树和模型树都是对预测值分段的树,主要论述如下:数据集中经常包含一些复杂的关系,使得输入数据和目标变量之间呈现非线性关系。对复杂关系建模,可以使用树来对预测值分段,包括分段常数或分段直线。相应的,若叶节点使用的模型是分段常数则称为回归树,若叶节点使用的模型是线性回归方程则称为模型树。使用不同的误差准则,就可以通过CART算法构建回归树和模型树。
CART算法构建的树倾向于对数据过拟合,一棵过拟合的树常常十分复杂,所以剪枝技术就出现了。两种剪枝方法分别是预剪枝(在树的构建中就进行剪枝)和后剪枝(当树构建完毕再剪枝),预剪枝更有效但需要用户定义一些参数。
书中写道:
本章是回归的最后一章!
接下来我们将离开监督学习的岛屿!
驶向无监督学习的未知港湾!
啊!星辰大海!