本文始发于个人公众号:TechFlow,原创不易,求个关注
今天是高等数学第11篇文章,我们来看看定积分的相关内容。
对于很多人来说定积分的内容其实早在高中就已经接触过了,比如在高中物理当中,我们经常使用一种叫做”微元法“的方法来解决一些物理问题。但实际上所谓的”微元法“本质上来说其实就是一种微积分计算方法。我们来看两个简单的例子。
微分与积分的例子
第一个例子是扇形的面积计算,先别急着笑,我知道这个是初中的内容。扇形的面积谁不会算,扇形的面积等于圆的面积乘上圆心角嘛。
圆的面积我们都知道\(S=\pi r^2\),如果是扇形的话,再加上圆心角,我们用弧度制来表示圆心角,可以直接进行计算:\(S=\pi r^2 \theta\)。
除此之外还有别的办法吗?
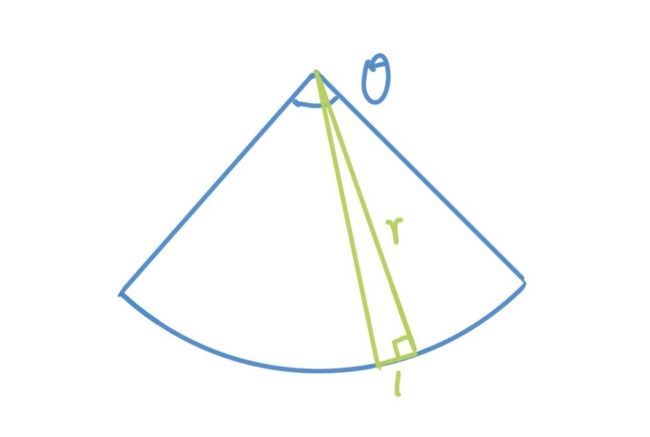
当然是有的,我们来看下面这张图:
在下面这张图当中,我们从扇形上切了一小块出来,做了一个直角三角形。我们令这个直角三角形无限窄,那么它的面积就可以近似于这一块小扇形的面积。
直角三角形的面积很简单,我们都会算,我们令短的直角边长度是l。那么这个小三角形的面积就等于\(\frac{1}{2}lr\)。
我们如此操作,可以把这一块扇形分割成无数个这样的小三角形,最后我们把这些小三角形的面积全部加起来,就可以得到扇形的面积。由于l趋向于0,每一个小三角形和小扇形的面积差的极限都是0,所以可以近似看成它们相等。
这样一番操作之后,我们可以用无数个小三角形的面积来代替扇形的面积。对于这些小三角形而言,它们的面积都是\(\frac{1}{2}lr\)。把它们进行累加,本质上也就是把这些所有的短边进行累加。那么显然,这些所有的短边累加之后的结果就是扇形的弧长。
我们假设这块扇形的弧长是L,那么整个扇形的面积还可以表示成\(\frac{1}{2}rL\)。
我们可以简单验证一下,一个完整的圆也可以看成是一个扇形。一个完整的圆,它的弧长,也就是周长是\(2\pi r\)。我们代入刚才的公式,得到的结果和圆的面积公式吻合,所以我们的计算是正确的。
在这个例子当中扇形分割成的每个小三角形是一样的,所以我们可以直接进行累加。如果我们微分之后的结果不再是固定的,是变化的,那么应该怎么办?
我们再来看另外一个例子:
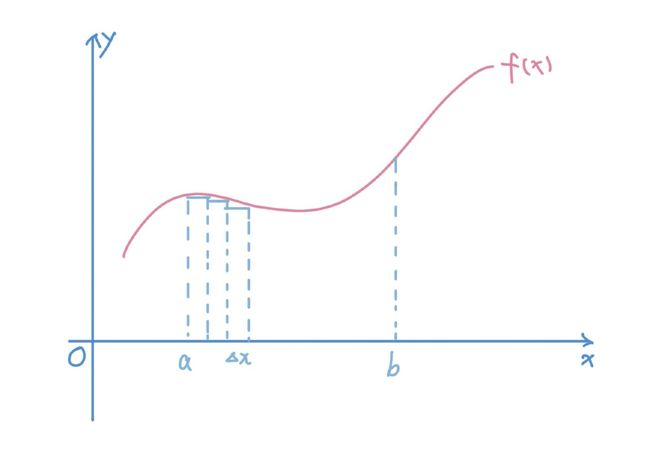
比如我们要求a和b两点围成的曲线矩形的面积,我们也可以将矩形进行拆分。我们可以无限拆分成多个小的矩形的面积去替代。我们可以很容易证明,当\(\Delta x\)趋向于0的时候,那一块小的矩形面积和曲线矩形的面积相等。所以我们可以把它拆分成无数个这样的矩形,然后将所有的面积求和,就得到了曲线围成的面积。
对于每一块矩形而言,它们的宽都是\(\Delta x\),但是它们的高都不相同。但是很容易看出来,它们的高都是区间里某一个坐标的函数值。其实我们可以写出来这些序列的值,它们分别是: a, a+\(\Delta x\), a + 2\(\Delta x\), ..., b。
为了方便书写,我们令这个序列等于\(\{\xi_1, \xi_2, \cdots, \xi_n\}\)
所以曲线围成的面积可以写成:
定积分的定义
我们观察一下上面这个问题,其实我们知道了很多信息,比如我们知道了函数f(x),我们还知道了a和b的值,看起来已经离结果很近了。的确如此,但是在我们继续往下之前,我们必须要明确一点,我们这样的推算是有前提的。
最大的也是隐藏的前提就是我们做的划分,我们必须要保证两点,首先我们要保证当\(\Delta x\)趋向于0的时候,矩形高度的极限是确定的。并且这些小矩形的面积和的极限趋近于它真实的面积。
我们用数学的语言来表达,也就是说,我们无论如何选取每一个\(\xi_i\),我们都要保证\(\lim_{\Delta x \to 0}\sum_{i=1}^n f(\xi_i) \Delta x\)是一个定值,这样我们就可以把这个式子写成定积分的形式:
这里的f(x)称作被积函数,\(f(x)dx\)称为被积表达式,x叫做积分变量,a和b分别称为积分的上限和下限。
如果f(x)在[a, b]上的定积分存在,那么就称为f(x)在区间[a, b]上可积。
什么样的函数可积呢?
这个问题要用数学的语言证明不太容易,但是如果从直观上去理解则要简单很多。通过上面的图,我们很轻松可以得到结论:连续函数一定可积,并且如果函数在[a, b]上有界并且只有有限个断点也可积。因为有限个间断点不会影响面积的计算,从这个角度入手,是否可积的判断其实还是很好理解的。
我们明白了可导的定义之后,我们再把之前连续和可导这些性质串起来,我们就可以编出高数顺口溜了:
可导一定连续,连续不一定可导。
连续一定可积,可积不一定连续。
可导一般可积,可积不一定可导。
理解并且记住这个顺口溜可是学好高数的基础,不信可以去问问考研党,这几句必然朗朗上口。如果觉得晕头转向也没关系,以后有机会会单独开一篇文章好好讲讲这几个顺口溜。
简单性质
最后,我们来看下定积分的一些简单性质。
第一个是加法性质,\(\int_a^b [f(x) \pm g(x)]dx = \int_a^b f(x)dx \pm \int_a^b g(x)dx\)
这个很好证明,我们只需要将它转化成累加的形式就可以把括号里相加的内容拆开:
另一个经常用到的性质是延续性质,假设f(x)在整个区间上可积,那么我们可以得到:
不论a,b,c之间的大小关系如何,上面的式子都成立。证明方法和刚才一样,我们将积分用累加形式来表示,代入即可。
最后一个性质是保号性,假设f(x)和g(x)在区间[a, b]上可积。并且对于任意x属于[a, b]都有\(f(x) \leq g(x)\),那么我们可以得到:\(\int_a^b f(x)dx \leq \int_a^b g(x)dx\).
这个证明也很简单,我们令\(h(x) = g(x) - f(x) \geq 0\),我们对h(x)进行积分,得到的结果自然大于等于0,再结合刚才的积分的加法性质,我们就可以移项得到结果了。
除了上面提到的三个性质之外,定积分还有很多其他的一些性质。但是这些性质一则比较琐碎,另外也比较直观,值得研究的内容不太多,所以我们不过多涉入,感兴趣的同学可以自行了解。
不知道看了这么多你是不是会有一些问号呢,我们分析了这么多,那么定积分究竟应该怎么计算呢?
这个问题先不着急回答,因为如果你学过微积分的话,那么对于怎么计算积分应该还有一些印象。如果没有的话,直接给出结论并没有什么用,在数学上结论总是需要我们通过严谨的推导的,否则就是空中楼阁,即使记住了,以后也总会忘记的。所以关于定积分的计算推导过程,我们放到下一篇文章当中,敬请期待啦。
今天的文章就是这些,如果觉得有所收获,请顺手点个关注或者转发吧,你们的举手之劳对我来说很重要。