运行要求
运行时间限制: 2sec
内存限制: 1024MB
原文链接
题目
有一个树状图由N个顶点和M条边组成。这个树状图的M条边里,不含有2重边和自我循环边。
第i(1<=i<=M)条边,连接着顶点ai和bi。
如有有一条边,去掉它,整个树状图就不能连接起来的话,这条边就称为桥。
求M条边中,桥的数量。
注:
- 自我循环的边:编号为i的边,ai=bi(1<=i<=M)
- N-1 <= M <= min(N(N-1)/2 , 50)
- 1<=ai < bi <= N
- 给出的树状图,不包含2重边和自我循环边
- 给出的树状图是连接起来的
输入
输入都以以下标准从命令行输入
N M
a1 b1
a2 b2
a3 b3
.
.
aM bM输出
M条边中,桥的个数
例1
输入
7 7
1 3
2 7
3 4
4 5
4 6
5 6
6 7输出
4给出的树形图如下图所示
图中,红色的边为桥,总共有4条
例2
输入
3 3
1 2
1 3
2 3输出
0桥不存在的情况也有
例3
输入
6 5
1 2
2 3
3 4
4 5
5 6输出
5所有的边都是桥的情况也存在
读懂题目
给出了N个点
给出了M条边
这M条边连接了N个点
不含有2重边(M条边里没有重复的边)
不含有自我循环边。(M条边里每条边都是连接两个不同的点)
解题思路
树状图的题目,直觉上可以用深度遍历(DFS)和广度遍历(BFS)来解决。但是遍历我们能够做到的就是遍历,如何和题目要求的桥的数量连接起来呢?
我们来看桥的定义(如果没有桥,树状图不能连接起来)
也就是说,如果有一条边Mi,有Mi这条边的话树状图可以连接,没有Mi这条边的话,树状图就不能连接。
DFS和BFS里,有一个节点状态的概念。
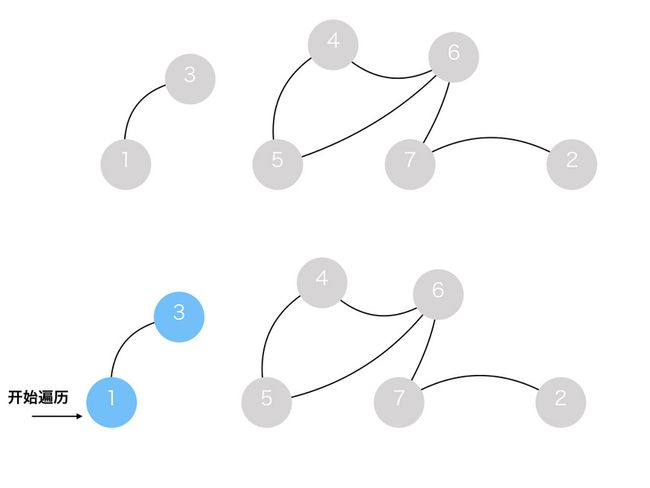
如图所示,
灰色代表节点还没有被遍历到。
蓝色代表节点已经被遍历到了。
开始遍历前,所有的节点的状态都是灰色。
遍历后,被遍历过的节点的状态是蓝色。
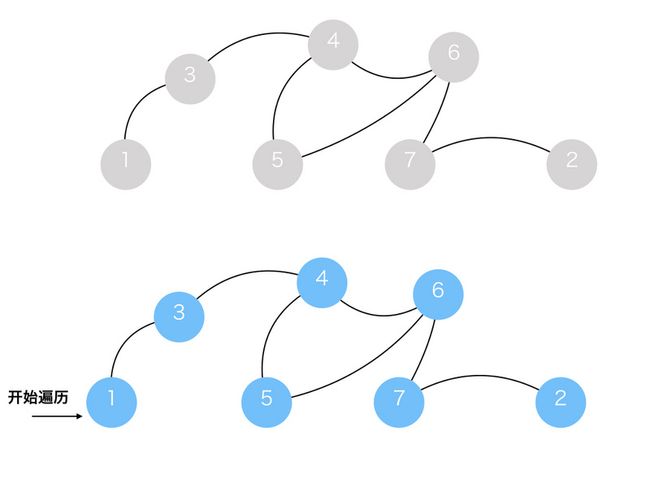
如果一个树状图里面的节点是相互连接的话,那么选取任意一个点开始遍历,所有的点都会被遍历到,所有的点的状态都会是蓝色

如图所示,我们拆掉一个不是桥的边(4-6),从1开始遍历,最后所有的点还是被遍历到
如图所示,我们拆掉一个桥的边(3-4),从1开始遍历,最后不是所有的点都被遍历到
所以,我们可以遍历M条边,每拆一条边,看看最后所有的点是否被遍历到。如果没有全部被遍历到,那么这条边为桥
遍历的方法,有DFS和BFS。这里我们给出两种解法
代码
DFS
S = input().split(" ")
N = int(S[0])
M = int(S[1])
ARR = []
for i in range(M):
ARR.append([int(s) for s in input().split(" ")])
def prepare(n, m, arr):
nodes = [[] for i in range(n)]
nodeStates = [0 for i in range(n)]
for i in range(m):
nodeFrom = arr[i][0] - 1
nodeTo = arr[i][1] - 1
nodes[nodeFrom].append(nodeTo)
nodes[nodeTo].append(nodeFrom)
return nodes, nodeStates
nodes, nodeStates = prepare(N, M, ARR)
def dfs(currentNodeIndex, arr, nodeStates):
if nodeStates[currentNodeIndex] == 0:
nodeStates[currentNodeIndex] = 1
childNodes = arr[currentNodeIndex]
for childNodeIndex in childNodes:
if nodeStates[childNodeIndex] == 0:
dfs(childNodeIndex, arr, nodeStates)
return nodeStates
# dfs(0, nodes)
def calculate(n, m, arr):
arr = list(arr)
result = 0
for ar in arr:
brr = arr.copy()
brr.remove(ar)
nodes, nodeStates = prepare(n, m-1, brr)
nodeStatesResult = dfs(0,nodes,nodeStates)
if sum(nodeStatesResult) != n:
result = result + 1
print(result)
calculate(N,M,ARR)
BFS
from collections import deque
S = input().split(" ")
N = int(S[0])
M = int(S[1])
ARR = []
for i in range(M):
ARR.append([int(s) for s in input().split(" ")])
def prepare(n, m, arr):
nodes = [[] for i in range(n)]
nodeStates = [0 for i in range(n)]
for ar in arr:
nodeFrom = ar[0] - 1
nodeTo = ar[1] - 1
nodes[nodeFrom].append(nodeTo)
nodes[nodeTo].append(nodeFrom)
return nodes, nodeStates
def bfs(startNodeIndex, arr, nodeStates):
q = deque()
q.append(startNodeIndex)
nodeStates[startNodeIndex] = 1
while q.__len__() > 0:
nodeIndex = q.popleft()
childNodes = arr[nodeIndex]
for childNodeIndex in childNodes:
if nodeStates[childNodeIndex] == 0:
q.append(childNodeIndex)
nodeStates[childNodeIndex] = 1
return nodeStates
def calculate(n, m, arr):
arr = list(arr)
result = 0
for ar in arr:
brr = arr.copy()
brr.remove(ar)
nodes, nodeStates = prepare(n, m-1, brr)
nodeStates = bfs(0, nodes, nodeStates)
if sum(nodeStates) != n:
result = result + 1
print(result)
calculate(N, M, ARR)
总结
这一题是基于遍历的求解,可以练习DFS和BFS