之前写的一篇 《初试 贝塞尔曲线》，如果您感兴趣可以看看，是关于贝塞尔曲线的基础用法。
最近看了很多有关贝塞尔曲线的文章，感觉大神们都好屌，文章都写的好好，就是有的时候注释写的不太够，理解起来有点费劲，所以我打算研读过后，补充注释，以便其他同学方便学习～～
效果图
开始本文之前先查看一下目标效果是如何的。
69b7d63agw1evxh2kw1bcg20m80go1l2.gif
这个动画的来源是优秀网页设计的一个微博，看到这个效果感觉下面的圆的动画十分的赞，于是就打算模仿这个效果。
然后接下来看我所做的简单效果吧。
111.gif
因为时间缘故就简单的模仿了自己感兴趣的主要效果，并没有做到全部模仿，等以后有时间了再完善
贝塞尔曲线知识讲解
将这个圆的动画效果拆解开看的画，其实会分为5个状态。
状态1.png
状态2.png
状态3.png
状态4.png
状态5.png
注：我这里的状态4和状态5其实与原设计图是有出入的，我这里的5个状态其实是对称关系的，但是原设计图并非是对称关系，然后因为我偷懒，就做成了对称设计，这个以后再优化吧~
也就是说，这个动画效果的实现就是不同状态之间的转化加上水平位移的实现，现在已经将动画肢解完了，那么接下来就讲解下如何实现圆的形变吧。
开始讲解具体内容之前我们需要先了解一下如何用贝塞尔曲线画一个圆，因为我的做法是通过贝塞尔曲线来实现的。
aEsuA.png
上图是stackoverflow上的一个答案，这个答案可能说的不是很清楚，这里还有一篇文章，这两个的结果都是差不多，就是所需要的数值c约等于0.551915024494f，具体的论证过程可以看这两篇文章，那么这个c的值有什么用么，我用最简单的方法来说明，就是把图中的1理解为圆的半径，那么对应的另外个值就应该是半径乘以0.551915024494f。
可能有朋友还是看不懂这个c到底干啥用呢，我下面画一个图来描述下，大概是怎么个意思。
jiangjietu.png
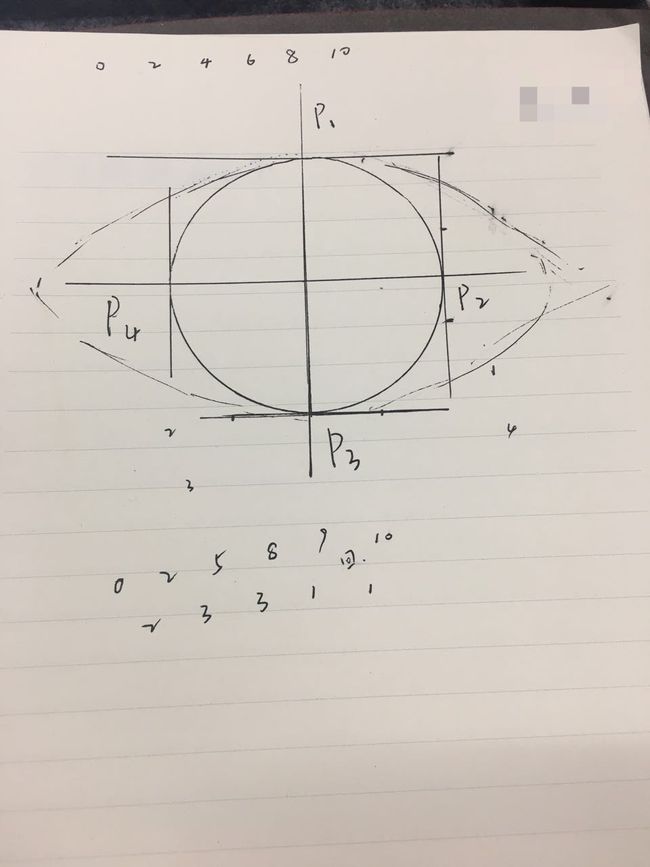
这里的坐标轴也就是Android中的坐标轴了，如果我们打算用贝塞尔曲线来画这么一个圆的话，我们需要知道这个圆的半径，以及图中的M的值，知道这两个值的话就能够知道图中12个点的坐标，知道坐标就能够用Path的cubicTo方法来使用贝塞尔曲线画出圆了。
这里稍微展示点代码来说明如何绘制P0至P3这段圆弧。
mPath.moveTo(p0.x,p0.y);
mPath.cubicTo(p1.x, p1.y, p2.x, p2.y, p3.x,p3.y);
这样我们就知道如何使用贝塞尔曲线来绘制一个圆了。也就是状态1和状态5我们都会绘制了，接下来看看状态2如何绘制。
1.jpg
通过上图大家就能很快的明白状态2应该如何绘制，其实就是把右边的点向右移动点距离就行了。
其实photoshop(sketch)这些绘图软件中的钢笔工具(Vector)就是用的贝塞尔曲线，然后这里推荐个网址给大家，轻松上手钢笔工具的使用哦，强烈推荐！！！
看完上面的讲解，那么状态3也就一点都不难了。
jiangjietu3.png.jpg
看到上图就明白状态3的实现就是在状态2的基础上修改了个值，一个是M的值加大，让圆看起来跟肥一点，还有就是圈住的那些点向右移动，做到居中。
至此，这个动画效果的分解也就完成了，其实一点都不难。最后还剩一个回弹，我的做法就是加个sin函数来控制，比较简单 。
示例代码
代码中的四个点，方便理解
代码中的四个点，方便理解.jpeg
/**
* Created by liuboyu on 17/1/12.
*/
public class MagicCircleView extends View implements View.OnClickListener {
private Path mPath;
private Paint mFillCirclePaint;
/**
* View的宽度
**/
private int width;
/**
* View的高度，这里View应该是正方形，所以宽高是一样的
**/
private int height;
/**
* View的中心坐标x
**/
private int centerX;
/**
* View的中心坐标y
**/
private int centerY;
private float maxLength;
/**
* 平移动化时间（值总在0-1之间）
*/
private float mInterpolatedTime;
/**
* 拉伸长度
*/
private float stretchDistance;
/**
* 圆球半径
*/
private float radius;
private float c;
private float blackMagic = 0.551915024494f;
private VPoint p2, p4;
private HPoint p1, p3;
public MagicCircleView(Context context) {
super(context);
init();
}
public MagicCircleView(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
public MagicCircleView(Context context, AttributeSet attrs, int defStyleAttr) {
super(context, attrs, defStyleAttr);
init();
}
/**
* 初始化
*/
private void init() {
mFillCirclePaint = new Paint();
mFillCirclePaint.setColor(0xFFfe626d);
mFillCirclePaint.setStyle(Paint.Style.FILL);
mFillCirclePaint.setStrokeWidth(1);
mFillCirclePaint.setAntiAlias(true);
mPath = new Path();
p2 = new VPoint();
p4 = new VPoint();
p1 = new HPoint();
p3 = new HPoint();
}
/**
* 初始化圆的各个点
*/
private void initCirclePoint() {
p1.setY(radius);
p3.setY(-radius);
p3.x = p1.x = 0;
p3.left.x = p1.left.x = -c;
p3.right.x = p1.right.x = c;
p2.setX(radius);
p4.setX(-radius);
p2.y = p4.y = 0;
p2.top.y = p4.top.y = -c;
p2.bottom.y = p4.bottom.y = c;
setOnClickListener(this);
}
/**
* 绘图
*/
private void drawCircle(float interpolatedTime) {
if (mInterpolatedTime >= 0 && mInterpolatedTime <= 0.2) {
drawCircleStatus_1(interpolatedTime);
} else if (mInterpolatedTime > 0.2 && mInterpolatedTime <= 0.5) {
drawCircleStatus_2(interpolatedTime);
} else if (mInterpolatedTime > 0.5 && mInterpolatedTime <= 0.8) {
drawCircleStatus_3(interpolatedTime);
} else if (mInterpolatedTime > 0.8 && mInterpolatedTime <= 0.9) {
drawCircleStatus_4(interpolatedTime);
} else if (mInterpolatedTime > 0.9 && mInterpolatedTime <= 1) {
drawCircleStatus_5(interpolatedTime);
}
}
/**
* 状态1
*
* @param interpolatedTime 为当前动画帧对应的相对时间，值总在0-1之间
*/
private void drawCircleStatus_1(float interpolatedTime) {//0~0.2
initCirclePoint();
p2.adjustAllX(stretchDistance * interpolatedTime * 5);
}
/**
* 状态2
*
* @param interpolatedTime 为当前动画帧对应的相对时间，值总在0-1之间
*/
private void drawCircleStatus_2(float interpolatedTime) {//0.2~0.5
drawCircleStatus_1(0.20f);
p4.adjustAllX(-stretchDistance * (interpolatedTime - 0.2f) * (10f / 3));
}
/**
* 状态3
*
* @param interpolatedTime 为当前动画帧对应的相对时间，值总在0-1之间
*/
private void drawCircleStatus_3(float interpolatedTime) {//0.5~0.8
drawCircleStatus_2(0.5f);
p2.adjustAllX(-stretchDistance * (interpolatedTime - 0.5f) * (10f / 3));
}
/**
* 状态4
*
* @param interpolatedTime 为当前动画帧对应的相对时间，值总在0-1之间
*/
private void drawCircleStatus_4(float interpolatedTime) {//0.8~0.9
drawCircleStatus_3(0.8f);
p4.adjustAllX(stretchDistance * (interpolatedTime - 0.8f) * 10);
}
/**
* 状态5
*
* @param interpolatedTime 为当前动画帧对应的相对时间，值总在0-1之间
*/
private void drawCircleStatus_5(float interpolatedTime) {
drawCircleStatus_4(0.9f);
interpolatedTime = interpolatedTime - 0.9f;
p4.adjustAllX((float) (Math.sin(Math.PI * interpolatedTime * 10f) * (2 / 10f * radius)));
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
mPath.reset();
canvas.translate(2 * radius, radius);
drawCircle(mInterpolatedTime);
// 平移
float offset = maxLength * (mInterpolatedTime - 0.2f);
offset = offset > 0 ? offset : 0;
p1.adjustAllX(offset);
p2.adjustAllX(offset);
p3.adjustAllX(offset);
p4.adjustAllX(offset);
// 圆球效果
mPath.moveTo(p1.x, p1.y);
mPath.cubicTo(p1.right.x, p1.right.y, p2.bottom.x, p2.bottom.y, p2.x, p2.y);
mPath.cubicTo(p2.top.x, p2.top.y, p3.right.x, p3.right.y, p3.x, p3.y);
mPath.cubicTo(p3.left.x, p3.left.y, p4.top.x, p4.top.y, p4.x, p4.y);
mPath.cubicTo(p4.bottom.x, p4.bottom.y, p1.left.x, p1.left.y, p1.x, p1.y);
canvas.drawPath(mPath, mFillCirclePaint);
}
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
width = w;
height = h;
centerX = width / 2;
centerY = height / 2;
radius = 100;
c = radius * blackMagic;
stretchDistance = radius;
maxLength = width - radius - radius;
}
@Override
public void onClick(View v) {
startAnimation();
}
class VPoint {
public float x;
public float y;
public PointF top = new PointF();
public PointF bottom = new PointF();
public void setX(float x) {
this.x = x;
top.x = x;
bottom.x = x;
}
public void adjustY(float offset) {
top.y -= offset;
bottom.y += offset;
}
public void adjustAllX(float offset) {
this.x += offset;
top.x += offset;
bottom.x += offset;
}
}
class HPoint {
public float x;
public float y;
public PointF left = new PointF();
public PointF right = new PointF();
public void setY(float y) {
this.y = y;
left.y = y;
right.y = y;
}
public void adjustAllX(float offset) {
this.x += offset;
left.x += offset;
right.x += offset;
}
}
/**
* 重写动画
*/
private class MoveAnimation extends Animation {
@Override
protected void applyTransformation(float interpolatedTime, Transformation t) {
super.applyTransformation(interpolatedTime, t);
// interpolatedTime 为当前动画帧对应的相对时间，值总在0-1之间
mInterpolatedTime = interpolatedTime;
invalidate();
}
}
public void startAnimation() {
mPath.reset();
mInterpolatedTime = 0;
MoveAnimation move = new MoveAnimation();
move.setDuration(3000);
move.setInterpolator(new AccelerateDecelerateInterpolator());
startAnimation(move);
}
}
在看代码的时候，可能会比较蒙，分状态画圆球的时候，有的＊10，有的＊5，有的又＊ (10f / 3)，其实很好懂，只是为了把时间变化值调整为0-1，以便相乘来操作距离的变化
拿状态1举例吧
/**
* 状态1
*
* @param interpolatedTime 为当前动画帧对应的相对时间，值总在0-1之间
*/
private void drawCircleStatus_1(float interpolatedTime) {//0~0.2
initCirclePoint();
p2.adjustAllX(stretchDistance * interpolatedTime * 5);
}
p2.adjustAllX(stretchDistance * interpolatedTime * 5);
状态1 中,在时间后面乘了个 5，因为状态一，时间上是 0～0.2，为了拉伸一整个stretchDistance，所以乘了个5，其他状态以此类推。
行了，后续还会更新相关贝塞尔曲线的文章，如果您喜欢，请关注～～