数值代数

第一次数值代数上机作业

---

一.

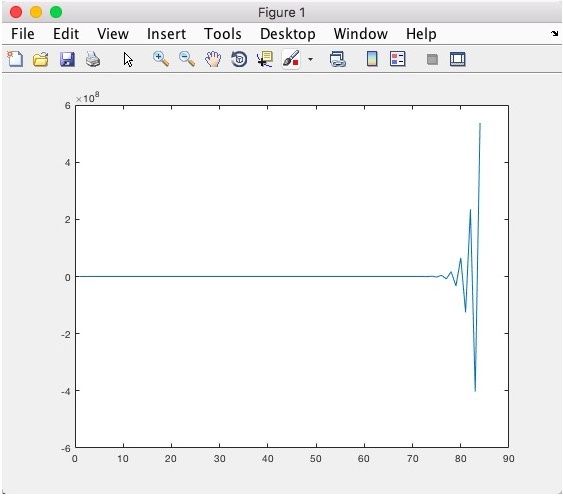
(1)不选主元的高斯消元法

A=6*eye(84)+diag(8*ones(1,83),-1)+diag(ones(1,83),1);
b=[7;15*ones(82,1);14];

n=length(A);
for k=1:n-1
    A(k+1:n,k)=A(k+1:n,k)/A(k,k);
    A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n);
end
L=tril(A,-1)+eye(n);
U=triu(A);

for j=1:n-1
    b(j)=b(j)/L(j,j);
    b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j);
end
b(n)=b(n)/L(n,n);

y=b;

for j=n:-1:2
    y(j)=y(j)/U(j,j);
    y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j);
end
y(1)=y(1)/U(1,1);
x=y

结果:

屏幕快照 2017-03-21 下午8.50.30

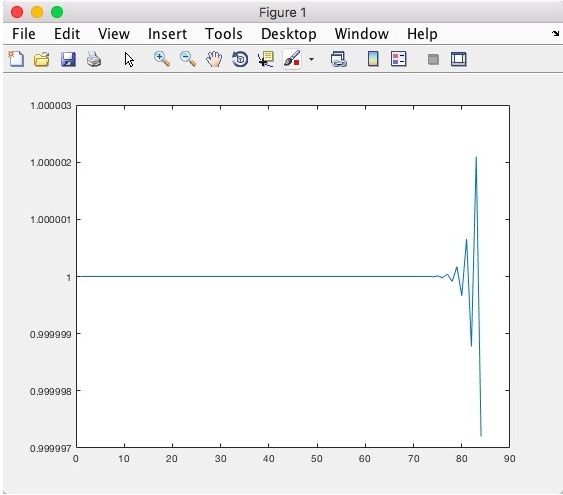
(2)列主元

A=6*eye(84)+diag(8*ones(1,83),-1)+diag(ones(1,83),1);
b=[7;15*ones(82,1);14];
n=length(A);
for k=1:n-1
    [s,t]=max(abs(A(k:n,k)));%求第k列最大值p与位置q
    p=t+k-1;%转化为在A中的坐标
    temp1=A(k,:);%A的k与q行交换
    A(k,:)=A(p,:);
    A(p,:)=temp1;
    temp2=b(k);
    b(k)=b(p);
    b(p)=temp2;
    if (A(k,k)~=0)
    A(k+1:n,k)=A(k+1:n,k)/A(k,k);
    A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n);
    else
        stop;
    end
end

L=tril(A,-1)+eye(n);
U=triu(A);

for j=1:n-1
    b(j)=b(j)/L(j,j);
    b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j);
end
b(n)=b(n)/L(n,n);

y=b;%y

for j=n:-1:2
    y(j)=y(j)/U(j,j);
    y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j);
end
y(1)=y(1)/U(1,1);

x=y

结果:

屏幕快照 2017-03-21 下午8.49.30

结论:列主元gauss消元法更加精确,且稳定性更好.

二.

(1)平方根法

A=10*eye(100)+diag(ones(1,99),1)+diag(ones(1,99),-1);
b=round(100*rand(100,1));
n=length(A);
for k=1:n
    A(k,k)=sqrt(A(k,k));
    A(k+1:n,k)=A(k+1:n,k)/A(k,k);
    for j=k+1:n
        A(j:n,j)=A(j:n,j)-A(j:n,k)*A(j,k);
    end
end
L=tril(A);
U=L';

for j=1:n-1
    b(j)=b(j)/L(j,j);
    b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j);
end
b(n)=b(n)/L(n,n);

y=b

for j=n:-1:2
    y(j)=y(j)/U(j,j);
    y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j);
end
y(1)=y(1)/U(1,1);
x=y;

（2）改进后的算法

A=10*eye(100)+diag(ones(1,99),1)+diag(ones(1,99),-1);
b=round(100*rand(100,1));
n=length(A);
for j=1:n
    for i=1:n
        v(i,1)=A(j,i)*A(i,i);
    end
    A(j,j)=A(j,j)-A(j,1:j-1)*v(1:j-1,1);
    A(j+1:n,j)=(A(j+1:n,j)-A(j+1:n,1:j-1)*v(1:j-1,1))/A(j,j);
end
L=tril(A);
D=diag(diag(A));
L=L-diag(diag(L))+diag(ones(1,n));
U=D*L';

for j=1:n-1
    b(j)=b(j)/L(j,j);
    b(j+1:n)=b(j+1:n)-b(j)*L(j+1:n,j);
end
b(n)=b(n)/L(n,n);

y=b

for j=n:-1:2
    y(j)=y(j)/U(j,j);
    y(1:j-1)=y(1:j-1)-y(j)*U(1:j-1,j);
end
y(1)=y(1)/U(1,1);
x=y;