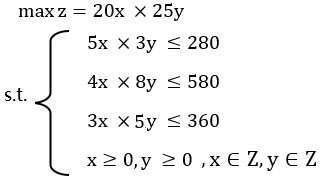很久没更新过APS系列文章了，这段时间项目工作确实非常紧，所以只能抽点时间学习一下运筹学的入门知识，算是为以后的APS项目积累点基础。看了一些运筹学的书（都是科普级别的）发现原来我目前面对的很多排产、排班、资源分配和路线规划问题，都是运筹学上的典型案例。与此同时，除了继续使用Optaplanner来做我们的规划类项目外，还花点时间去研究了一下Google OR-Tools开源规划引擎，这是Google旗下的一个开源求解器，接下来我会专门写一些关于Google OR-Tools应用的文章，并与Optaplanner作些关联对比。
本篇先向大家展示一下两个规划工具，在求解线性规划问题上的应用方法，分别是Microsoft Office的Excel里的”规划求解”组件和Google Dos中的Spreadsheet上提供的Linear Optimization插件。这两个工具都可以作为规划问题的求解器。因为它们是以插件或软件功能形式提供的，在灵活性和扩展性方面限制还是比较大，但是因为不涉及软件开发的技能，普通用户都能很好地应用它们来解决一些现实业务中遇到的规则问题。
因为Google的Linear Optimization是Google文件服务中的Spreadsheet（Google提供的类似于Excel的电子表格程序），因为目前国内的网络情况（你懂的），访问它需要自己想办法，我们公司总部不在中国境内，所以我们的办公网络经过注册，是可以合法访问外界的；关于网方面不在本篇中讨论，大家自己科学解决就可以了。
规划问题
下面先给出本次我们需要求解的线性规划问题，其实在Optaplanner相关的文章中，详细介绍过关于NPC问题，普通线性规划问题很多并不是NPC问题，因为对于线性规划模型，还是有例如单纯形法等算法推算它的最优解的，而不是所有规划问题的时间复杂度都是O(a^n)或O(n!)的，大家要理解清楚两者的关系。
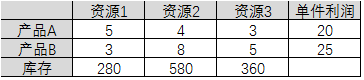
我们要求解的问题跟很多运筹学教材或科普书籍上的例子一样，也是最简单的在确定的条件约束下，求最大利润下的产品生产方案问题。例如一家工厂生产两种产品，产品A与产品B，均需使用到三种资源，资源1、资源2和资源3。其中生产一件产品A，需要5个单位的资源1，4个单位的资源2，3个单位的资源3。生产一件产品B需要3个单位的资源1，8个单位的资源2，5个单位的资源3。一个产品A的利润是20，一个产品B的利润是25。库存中三种资源的存量为：280单位的资源1，580单位的资源2，360单位的资源3.见下表：
求：两种产品分别生产多少件，才能令到总利润最大？此时的利润是多少？
以上问题是典型的线性规划问题，运筹学的同学可以通过单纯形法进行求解，但是这种方法对于没有运筹学背景的普通工程师来说，困难还是不小。即使我们学会这种办法，但遇到更复杂问题的时候，对我们来说其挑战还是相当大。因此，目前市上，或开源世界里，提供了很多解决此类规划问题的开源软件。但对于非IT人员来说，没有软件开发背景，很难利用这些开源软件工具写程序求解。因此，一些知名的办公软提供了相关的特性，让非IT专业人员直接使用其规划功能，输入数据即可快速求得答案。对各行业的生产、管理活动提供了极大的帮助。下面我们就以Excel和Google Spreadsheet两种工具中的规划求解功能，尝试求解上述问题。
对问题进行数学建模
要解决上述问题，就需要对问题进行线性规划建模，建立数学模型，以数学工具对问题的约束和目标进行归纳、抽象，用数学语言表达问题的本质意义。对于上面的问题我们的建模如下：假设产品A生产x件，产品B生产y件，才能让利润最大化。那么我们通过对问题的约条件和规划目标的分析，可以得出以下数学模型。
该模型表示：生产产品A和产品B所需的三种资源的总量，均不能超过每种资源的库存量；并且产品件数量必须是大于等于0的整数。规划的目标函数是找出两种产品的利润之和的最大值，并计算出获得该利润时，两种产品的产量分别是多少。
对于线性规划问题，其实可以通过单纯形法、对模型进行求解，从而得出z最大时的x与y的值。但此方法需要一定的数学知识，此范围的知识不在本文的讨论范围内，以后若有机会，我再简单介绍一下通过单纯形法对此模型求解步骤。但本人也不是运筹专业出身，估计也只是班门弄斧；因此，大家可以上网寻找更专业的运筹学资源，了解规划模型的解法。本文通过Excel下的规划求解功能，以及Google下的Spreadsheet中的Linear Optimization插件，对该规划模型进行求解，从而取得该生产安排问题的解。
Microsoft Excel规划求解
Excel提供了一个非常强大的组件用于解决此类规划问题，目前我还只尝试过线性规划问题，根据其资料显示，非线性规划也是可以解的。以后若有机会尝试一下其它规划问题再分享给大家。下面逐一展示这组件具体用法给大家。
第一步：添加“规则求解”组件
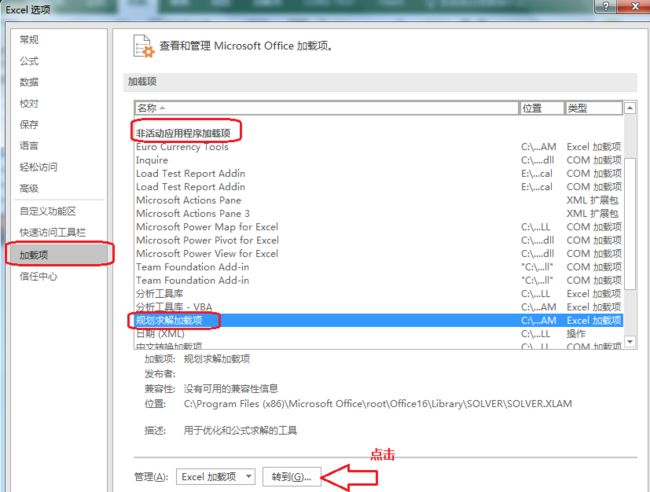
因为规则求解功能默认不会出现在Excel的常用工具栏中，因此，需要从加载项目中把它加载出来才能使用。在Excel菜单栏中，选择【文件】->【选项】，在弹出的【Excel选项】窗口中，选择【加载项】页签，在列表中的【非活动应用程序加载项】（意思是说Excel目前有这些功能可以用，但还没有加载进去，所以不会显示在工具栏中）的其下方找到【规则求解加载项】，如下图.
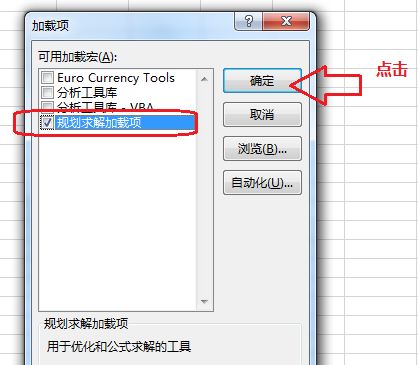
在列表下方的【管理(A)】下拉框中选择【Excel加载项】，点击【“转到...】按钮，会弹加载项窗口，如下图。在【可用加载宏(A)】列表中，选中【规划求解加载项】，点击确定，窗口关闭。
在Excel的【数据】工具栏的最右则，你会看到【规划求解】的图标，即是刚才我们操作完成后加载进来的组件，如下图。
事实上它是Microsoft提供的一个求解器，该组件对应的文件在C:\Program Files (x86)\Microsoft Office\root\Office16\Library\SOLVER此文件夹下。该文件夹下有两个文件，分别是SOLVER.XLAM和SOLVER32.DLL, SOLVER.XLAM是一个Excel的宏文件，用于实现Excel对求解器核心SOLVER32.DLL的调用，因此SOLVER32.DLL应该就是这个求解器的核心程序动态连接库。
第二步：将问题填入Excel表并建立各变量之间的关系
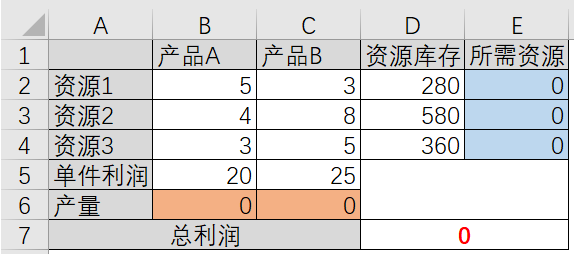
完成规划求解组件加载后，下面就可以将数学模型的各个常量、变量和约束关系填入Excel单元格中；先将两种产品和三种资源对应的使用数量建立一张二维表，如下表。
通过Excel及规划求解组件解答此问题步骤如下：
1.填入常量：上表中，产品A对资源1、资源2和资源3的要求量分别是5，4，3(即B2,B3,B4的值)，其单件利润为20(B5)。 同样方法将产品B对应的数量填入C２- C5单元格中。另外，对于三种资源的库存量，将其值填 入D2 - D4中。自此，模型中涉及的常量已经全部填写时表格。
2.根据数学模型，定义运算关系：本模型中，我们的目标是求得当z最大时变量x,y的值(x,y在运筹学的规划模型中被称为 决策变量；在Optaplanner中，它们被称作规划变量)。在Excel中每一个决策变量需要确定在一个单元格，以备参与接下来的规划计算，如上表的B6,C6单元格。在未启动规划的时候，这两个单元格直接填上0作为初始值即可。这两个代表决策变量的单元格在完成规划，找到答案后，运算结果值将会被填到对应的单元格中。
确定好这两个变量后，下一步需要考虑规划目标，也就是总利润最大化的目标，也需要为此目标值确定一个单元格，此单元格的值会在规划完成时，确定了B6和C6两件单元格的值之后计算出来。根据目标函数z = 20x X 25y的定义，此单元格的公式应为 ：B5 * B6 + C5 * C6，即两种产品的利润之和。我们把存储利润之和的值定在D7单元格，为了直观美观，我们把D7与E7合并。
确定了目标函数值的单元格和计算公式后，下一步需要处理约束条件，也就是产品的资源使用量与库存的约束关系。对于资源1，我们将E2确定为其资源用量，它计算公式应该是:B2 * B6 + C2 * C6,即两种产品对该资源的使用量之和。按相同的规则，设置E3 = B3 * B6+ C3* C6, E4 = B4 * B6 + C4 * C6.
第三步：设定规划求解逻辑参数
通过上述两个步骤设定后，各个单元格的常量值、决策变量和运算关系已设定好。接下来就可以启动【规划求解】插件进行逻辑设定。在【数据】菜单项目中，最右则的【分析】组里，有一个【规划求解】图标，点击它，即可打开【规划求解】窗口(如下图)
以下讲解这些参数意义及其设置。
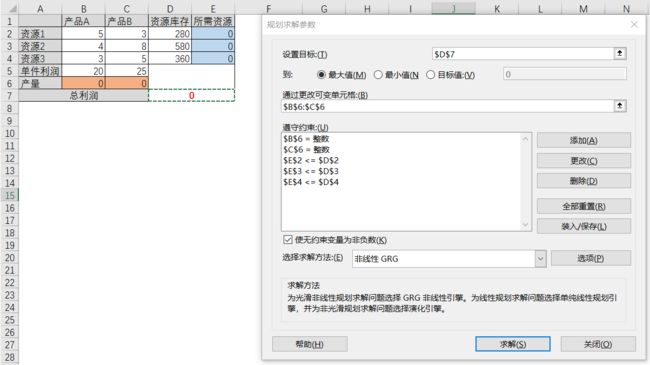
1.【设置目标(T)】项:该项目我们需要选定一个单元格，表示该单元格是本次规划活动需要计算的目标。通过问题描述和规划模型，我们得知该问题目标是求利润的最大值及取得该利润时两种产品的产量。也即模型中的目标函数z的最大值，及此时的x,y的值。在上表中D7就是存放这个目标函数的单元格，因此这里选中D7即可。在参数设置时，都是使用单元格的绝对地址，因此单元格地址前面都有$符号。
2.目标值中【到】项：该项用于设置对于目标函数的取值要求，可以看到它有【最大值】，【最小值】和【目标值】三个选项。其中【最大值】和【最小值】，表示目标函数往最大或最小两个极值方向求解，即最优解中，D7单元格的值是在满足约束条件情况下取得的最大值。而【目标值】则表示取得最优解时，目标函数值最等于或最接近于此值。本问题中的目标是求利润最大，所以我们选择【最大值】。
3.【通过更改可变单元格(B)】：该项表示在规划过程中求解器，通过改变哪些单元格的值，来获得结果，直到【目标值】所指的单远格（本例中的D7)中的值达到极值。对应到模型中，也就是x与y两个决策变量，本例中对应的单元格是B6和C6，分别表示产品A和产品B的产量。因此，选择B6和C6即可。
4.【遵守约束】：该项内容表示本次规划需要符合的约束条件，也就是模型中的s.t.部分(s.t. 是subject to的缩写)和各个不等式和各变量的范围条件。点击右则的【添加(A)】按钮，弹出【添加约束】窗口(如下图)，可以看到约束的表达方式非常简单，就是添加左右两则值的逻辑关系。
参照模型中的s.t.部分，和excel中的单元格位置关系，添加它们的关系即可。例如对于资源1，s.t.中的约束条件5x * 3y <= 280, 可参通过选择操作，添加以下关系: E2 <= D2，表示产品A所需资源量与产品B所需资源量之和，不能大于资源库存量。按相同的规则设置好资源2和资源3的约束条件。另外对于决策变量x,y，模型中有这两个变量应为整数，且大于等于0的约束。因此，分选选择B6和C6，并在条件表达关系选择int即可。完成后条件约束的内容如上图中的【遵守约束】列表中的内容。
5.【选择求解方法】：该栏列举了目前可选择的三种求解算法，分别是【单纯线性规划】，即单纯形解法，【非线性GRG】和【演化】。具体的求解方法在选择框下方有简单解释，我们选择默认的【非线性GRG】或【单纯形法】即可。
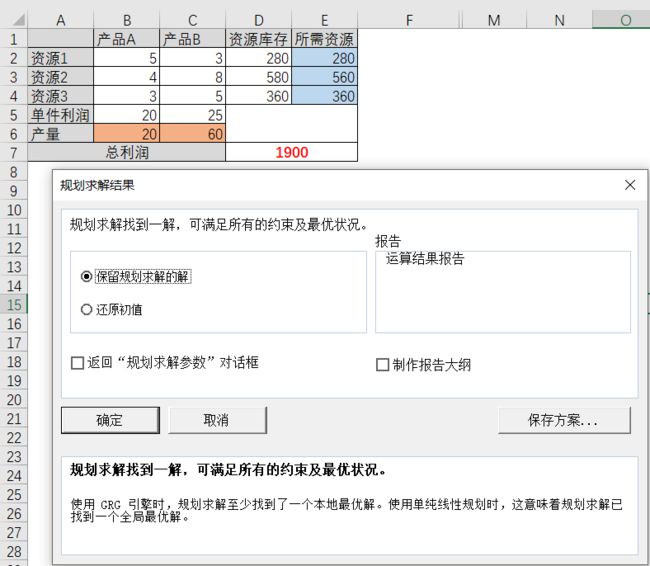
6.【求解】：点击【求解】按钮，即会启动求解器进行规划求解。完成后会弹出【规划求解结果】窗口，供进一步操作（例如保存规划方案等）。与此同时，原来在未求解前，因为产量设置为0，所以所需资源（E列）的三个单格E2,E3,E4,以及总利润单元格D7的初始值是0。完成规划后，找到最大利润下两种产品的产量(B6,C6)之后，上述原值为0的单元格的值，也随即被更新为该利润最大方案时对应的值。如下图。
由结果可知，完规划求解后，得到的决策变量值：x=20, y=60, 目标函数z的值为1900，即表示：当产品A生产20个(B6单元格)，产品B生产60(C6单元格)个时，其利润达到最大值1900(D7单元格)。上述规划问题得到完美解。下面我们再使用另外一个工具 - Google Spreadsheet中的线性优化插件，求解同样的问题。
Google Spreadsheet线性优化功能插件
对于规划问题，微软和Google通提供了很强大的套件，令到像我这种没有运筹学背景的普通用户，可以方便地求解一些规划问题。在此不得不感叹一下，在此方面国内类似软件与国外的差别。曾经有朋友跟我讨论过，公司使用的国内某个一线办公软件，功能直逼office，办公中绝大部分情况，这个软件都能处理，但遇到一些需要进行规划运算的问题，此软件则没有提供类似的功能，不得不求助于Microsoft Excel。
说到这种非专业人员用的规划求解工具，不得不延伸提一下规划引擎软件方面，也存同类问题。目前在国内，如果是针对某一大型公司或项目，只要资源到位，实现一个可用的规划引擎问题不算大。但涉及要求更高，可用性更强的通用规划引擎(无论是开源还是商业)国内外的差距就体现出来了。商业求解器领域暂不深入讨论，本人专注于开源规划引擎的应用 研究，近两三年项目应用或自己学习研究中，曾分析应用过一些开源规划引擎，除开优化性能和优化结果的质量上的比较；仅就在工程实践的可用性、易用性上，目前还很难在国内找到一款能跟Optaplanner及Google OR-Tools媲美的开源引擎。先不说可以满足建模要求的引擎软件包，就是求解器方面，国内开源项目也寥寥可数。
下面开始对Google Spreadsheet中的Linear Optimization插件的应用进行具体介绍。还是在上面已经建立好的数学模型基础上，讨论通过Google的Linear Optimization求解此模型。在开始之前，需要完成以下准备工作：
- 解决网络连接问题。这个大家懂的，大家可以自行想办法解决，如果一些在外资或需要访问国外网络的机构工作的朋友（如我们办公室是可能正常合法访问国外网络），则可以跳过此节。
- 注册Google帐号(若你未有Google帐号）。因为Google Docs，Google Spreadsheet均是类似于Microsoft Office的在线文件处理应用服务。无论是哪个Google服务，需要使用必须通过Google帐号。
完成上述前期工作后，即可开始Google Spreadsheet的配置和应用。
第一步：安装Linear Optimization(线性优化)插件
Linear Optimization是Google Spreadsheet的一个插件，可以实现对线性规划模型的求解。默认状态下，Google Spreadsheet是不包括此插件的，需要使用的话，则需要将期添加Spreadsheet中才能使用。下面将操作接步骤列出。
1.创建Spreedsheet文件
登录Google帐号，进入Google Sheets页面（http://sheets.google.com）。进入后Spreadsheet主页后，点击页面右下解的红色添加按钮，创建一个Google Spreadsheet文件。在创建好的文件中，可以将文件命名为“LP_Test”文件即会自动保存到你的Google帐号。如下图。
添加Spreadsheet 重命名文件
2. 添加Linear Optimization插件
通过Spreadsheet页面的Add-ons菜单，将Linear Optimization插件添加到你的帐号上，才能进一步使用该线性优化插件，可以看到还有更多规划功能的插入可以添加。这也是Google在运筹优化方面的系统架构与Optaplanner存在的差别。我将会有新的一篇文章对比两个开源规划引擎这方面的差异，敬请期待。点击Add-ons -> Get add-ons… 菜单项目，将会弹出【Add-ons】页面，在页面上的搜索框中输入”Linear Optimization”并回车，即可搜索出该插件,并点击【+FREE】按钮进行添加。如下图。
在添加过程中，需要你登录或选择一个已经登录的帐号,选择你已登录的帐号即可，如下图
选择或输入帐号后，会转到一个Sign in页面，大概意思是说Linear Optimization将会被添加到指定页面，点击页面底部右则的【Allow】按钮即可。
3. 创建线性规划模板
添加完成后，在【Add-ons】菜下会出现【Linear Optimization】子菜单项，该子菜单下会有用于设置决策变量、约束和求解的子项。见下图。
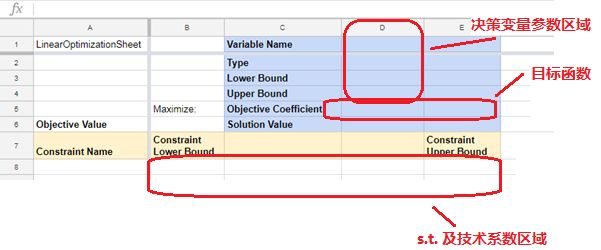
选择【Linear Optimization】菜单下的【Set up optimization sheet】子项，即可在当前Sheet中生成求解模板，模板中包含f了决策变量定义区域、目标函数区域和约束区域。下图为新创建的线性规划模板刚创建好的状态.
4.填入决策变量、约束和目标函数
创建好线性规划模板后，需要将上面已经建立好的数学规划模型输入模板中对应的单元格，正确地反映数学模型的意义，才启动求解器（Google的在线规划服务，是用通WebAPI提供的，因此其求解器是部署在Google自己的服务器上）。初学者可以通过Linear Optimization菜单下的子项，来辅助输入决策变量和约束。选择Linear Optimization菜单下的【Add Variables...】子项，在页面的右则会显示【Describe data】 页面。该页面中点击【Variables】和【Constrains】页签分别可以提供定义决策变量(即模型中的x,y)和约束条件(即模型中s.t.部分中的不等式)的输入元素。以下是【Variables】的各个字段输入如下：
a. Variable Name: 该字段表示决策变量，输入第一个决策变量名x.
b. Type: 从我们建立的规划模型中，知道决策变量x是一个整数，因此Type中选择Integer,(它默认是Continuous).
c. Lower bound, Upper bound:这两个字段分别表示约束变量的最大值与最小值（即决策变量的取值范围），从模型中可以看到它们的最小值是0, 且无最大值限制，因此，Lower bound填上0， Upper bound留空（它提示为Defaults to Infinity,大家应该懂了吧?)。
d. Objective coefficient:该字段表示该决策变量在目标函数中的系数，也就是目标函数表达式中，x前面的常数，从模型的目标函数上可以看到x前面的技术系数为20，因此填入20即可。点击【Add】按钮，x的相关值及其在目标函数上的体现将会被填入模板中。以相同的规则填入决策变量y相关的信息。
下面介绍约束的输入，点击【Constraints】页签，页面将会展示约束条件填入界面：
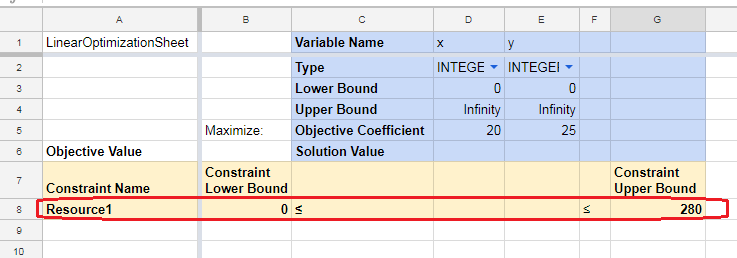
a. Constraint Name:因为现在我们是新建立约束，因此在下拉框中选择【New Constraint】, 页面中将会出同【Constraint Name】、【Lower bound】和【 Upper bound】三个字段。【Constraint Name】字段中输入一个名称用于标识该约束即可，因为模型中每个不等式是表示一种资源的限制，因此第一个不等式是针对资源1的库存限制的，我们输入”Resource1”。
b. Lower bound，Lower bound：以模型的s.t.部分中的首个不等式 
为例，其实我们根据题意可以把它补充成
，也就是说，模型中少了产品A资源用量大于等于０这个限制；其实这样是不严谨的。但因为目标函数是求最大值，因此，大于等于0这个条件不表示出来，也不会影响模型的正确性。但需要在Google的Linear Optimization中表未这个不等式时，必然存此条件才能完整表示，包括以后我们直接使用Google OR-Tools中的线性规划模块，不等式的必须有明确的范围才行。根据上面的不等式，我们在【Lower bound】中填入0，【Upper bound】输入280(即少于等于280)。点【Add】按钮，首个约束就会被添加到模板中，并添加了范围限制见下图红框内.此时,Resource1这一行(第8行)仅仅表示了式子的值域，具体的式子并未完成。
c. Variable Name, Coefficient:一上步仅添加了约束Resource1的基本结构。本步骤将要完成不等式中的式子部分。点击【Add】后，页面将会出现【Variable name】下拉框，其中有当前模型的所有决策变量(即本例中的x与y）供选择。在右则还会出现【Variable coefficient】输入框，表示你选择的决策变量在不等式中前面的常数（即技术系数），通过模型我们看到Resource1不等式中x前面的常数是5，因此填入5，并点击【Add】，此时常数5就会被填入当前约束，x对应列的单元格（即D8单元格)。同样地，不等式中决策变量y前面的常是3，因此我们在【Variable name】中选择y，并在【Variable coefficient】中填入3。点击【Add】即可完成约束Resource1的输入。同样的方法输入资源2和资源3的约束，完成后如下图
5.求解
完成上述步骤之后，我们建立的规划模型已经全部表达到Linear Optimization模板中，选中【Linear Optimization】菜单下的【Solve】子项，程序将会启用Google的线性规划Web服务，对刚才输入的模型进行求解，并把结果填回表格中，见下图.
上图是模型的规划结果，可以看到，通过这个模型计算出来的最大的利润是1900(B6单元格)，获得此利润时，产品A的产量是20(D6单元格)，产品B的产量是60(E6单元格).
写在最后
本文通过对一个简单的线性规划问题，建立线性规划模型；并分别通过Excel的规划求解组件，和Google Spreadsheet下的Linear Optimization插件对模型进行求解，从而得出最优结果。非IT专业人员在实际生产活动中，遇到此类线性规划问题时，可以通过此方法对问题进行求解。而专业的IT人员，遇到的问题会比本文中的情况复杂得多，通过现成的软件功能很可能是无法解决，需要通过软件开发技术，结合规划引擎进行求解。大家可以参考我之前的Optaplanner系列文章 .
本人近段时间也在研究Google OR-Tools，发现本文用到的Linear Optimization其实是通过将Google OR-Tools的多个运筹求解器，建立在Google自身的服务器上；再以Web服务方式提供给的。在实际软件项目开发过程中，我们可以绕开Google Spreadsheet服务程序，通过自己的程序调用其运筹优化服务进行求解。当然现目前国内的情况来看，通过对它的开源项目Google OR-Tools的引用，直接将其求解器纳入我们自己开发的系统中更现实。
我正在撰写一篇关于Optaplanner与Google OR-Tools的对比文章，通过对比两个引擎的用法，有针对性的引出对Google OR-Tools的应用，敬请期待，谢谢！
如需了解更多关于Optaplanner的应用，请发电邮致：[email protected]
或到讨论组发表你的意见：https://groups.google.com/forum/#!forum/optaplanner-cn
若有需要可添加本人微信（13631823503）或QQ(12977379)实时沟通，但因本人日常工作繁忙，通过微信,QQ等工具可能无法深入沟通，较复杂的问题，建议以邮件或讨论组方式提出。(讨论组属于google邮件列表，国内网络可能较难访问，需自行解决)