algo_预备

第一部分

预备知识

第1章 C + +程序设计

大家好！现在我们将要开始一个穿越" 数据结构、算法和程序" 这个抽象世界的特殊旅程，以解决现实生活中的许多难题。在程序开发过程中通常需要做到如下两点：一是高效地描述数据；二是设计一个好的算法，该算法最终可用程序来实现。要想高效地描述数据，必须具备数据结构领域的专门知识；而要想设计一个好的算法，则需要算法设计领域的专门知识。

在着手研究数据结构和算法设计方法之前，需要你能够熟练地运用 C + +编程并分析程序，这些基本的技能通常是从C + +课程以及其他分散的课程中学到的。本书的前两章旨在帮助你回顾一下这些技能，其中的许多内容你可能已经很熟悉了。

本章我们将回顾C++ 的一些特性。因为不是针对C++ 新手，因此没有介绍诸如赋值语句、 if 语句和循环语句（如for 和w h i l e）等基本结构，而是主要介绍一些可能已经被你忽略的 C + + 特性：

• 参数传递方式（如传值、引用和常量引用）。
• 函数返回方式（如返值、引用和常量引用）。
• 模板函数。
• 递归函数。
• 常量函数。
• 内存分配和释放函数：n e w与d e l e t e。
• 异常处理结构：t r y, c a t c h和t h r o w。
• 类与模板类。
• 类的共享成员、保护成员和私有成员。
• 友元。
• 操作符重载。

本章中没有涉及的其他C + +特性将在后续章节中在需要的时候加以介绍。本章还给出了如下应用程序的代码：

• 一维和二维数组的动态分配与释放。
• 求解二次方程。
• 生成n 个元素的所有排列方式。
• 寻找n个元素中的最大值。

此外，本章还给出了如何测试和调试程序的一些技巧。

 

目录：

1.1 引言    4

1.2 函数与参数    4

1.2.1 传值参数    4

1.2.2 模板函数    5

1.2.3 引用参数    6

1.2.4 常量引用参数    7

1.2.6 递归函数    8

    （1 - 1）    9

    （1 - 3）    10

练习    14

1.3 动态存储分配    15

1.3.1 操作符n e w    15

1.3.2 一维数组    15

1.3.3 异常处理    0

1.3.4 操作符d e l e t e    1

1.3.5 二维数组    1

图1-1 一个3× 5数组的存储结构    2

练习    4

1.4 类    4

1.4.1 类C u r r e n c y    4

1.4.2 使用不同的描述方法    12

unsigned int c)    13

1.4.3 操作符重载    0

1.4.4 引发异常    2

1.4.5 友元和保护类成员    3

不能访问p r i v a t e成员a m o u n t。我们可以把ostream& operator<<描述为C u r r e n c y类的友元，从而避免定义附加的函数，这样就把 C u r r e n c y所有成员（包括p r i v a t e成员及p u b l i c成员）的访问权都授予了该函数。为了产生友元，需要在 C u r r e n c y类描述中引入friend 语句。为一致起见，总是把friend 语句放在类标题语句中，如：    3

1.4.6 增加#ifndef, #define和# e n d i f语句    4

练习    5

1.5 测试与调试    5

1.5.1 什么是测试    5

1.5.2 设计测试数据    8

1.5.3 调试    11

1.6 参考及推荐读物    12

 

 

1.1 引言

在检查程序的时候我们应该问一问：

• 它正确吗？
• 它容易读懂吗？
• 它有完善的文档吗？
• 它容易修改吗？
• 它在运行时需要多大内存？
• 它的运行时间有多长？
• 它的通用性如何？能不能不加修改就可以用它来解决更大范围的问题？
• 它可以在多种机器上编译和运行吗？或者说需要经过修改才能在不同的机器上运行吗？上述问题的相对重要性取决于具体的应用环境。比如，如果我们正在编写一个只需运行一次即可丢弃的程序，那么主要关心的应是程序的正确性、内存需求、运行时间以及能否在一台机器上编译和运行。不管具体的应用环境是什么，正确性总是程序的一个最重要的特性。一个不正确的程序，不管它有多快、有多么好的通用性、有多么完善的文档，都是毫无意义的（除非它变正确了）。尽管我们无法详细地介绍提高程序正确性的技术，但可以为大家提供一些程序正确性的验证方法以及公认的一些良好的程序设计习惯，它们可以帮助你编写正确的代码。

我们的目标是教会你如何开发正确的、精致的、高效的程序。

1.2 函数与参数

1.2.1 传值参数

考察函数A b c（见程序1 - 1）。该函数用来计算表达式 a+b+b*c+ (a+b-c) / (a+b) + 4，其中a，b 和c 是整数，结果也是一个整数。

程序1-1 计算一个整数表达式

int Abc(int a, int b, int c)

{

return a+b+b*c+(a+b-c)/(a+b)+4;

}

在程序1 - 1中，a，b和c 是函数Abc 的形式参数（formal parameter），类型均为整型。如果在如下语句中调用函数A b c：

z = Abc(2,x,y)

那么，2，x 和y 分别是对应于a，b 和c 的实际参数（actual parameter）。当A bc( 2 ,x,y) 被执行时，a 被赋值为2；b 被赋值为x；c 被赋值为y。如果x 和 / 或y 不是int 类型，那么在把它们的值赋给b 和c 之前，将首先对它们进行类型转换。例如，如果x 是float 类型，其值为3 . 8，那么b 将被赋值为3。在程序1 - 1中，形式参数a，b 和c 都是传值参数（value parameter）。

运行时，与传值形式参数相对应的实际参数的值将在函数执行之前被复制给形式参数，复制过程是由该形式参数所属数据类型的复制构造函数（ copy constructor）完成的。如果实际参数与形式参数的数据类型不同，必须进行类型转换，从实际参数的类型转换为形式参数的类型，当然，假定这样的类型转换是允许的。

当函数运行结束时，形式参数所属数据类型的析构函数（d e s t r u c t o r）负责释放该形式参数。当一个函数返回时，形式参数的值不会被复制到对应的实际参数中。因此，函数调用不会修改实际参数的值。

1.2.2 模板函数

假定我们希望编写另外一个函数来计算与程序 1 - 1相同的表达式，不过这次 a，b和c是f l o a t 类型，结果也是f l o a t类型。程序1 - 2中给出了具体的代码。程序1 - 1和1 - 2的区别仅在于形式参数以及函数返回值的数据类型。

程序1-2 计算一个浮点数表达式

float Abc(float a, float b, float c)

{

return a+b+b*c+(a+b-c)/(a+b)+4;

}

实际上不必对每一种可能的形式参数的类型都重新编写一个相应的函数。可以编写一段通用的代码，将参数的数据类型作为一个变量，它的值由编译器来确定。程序 1 - 3中给出了这样一段使用t e m p l a t e语句编写的通用代码。

程序1-3 利用模板函数计算一个表达式

template<class T>

T Abc(T a, T b, T c)

{

return a+b+b*c+(a+b-c)/(a+b)+4;

}

利用这段通用代码，通过把T替换为i n t，编译器可以立即构造出程序1 - 1，把T 替换为f l o a t 又可以立即构造出程序 1 - 2。事实上，通过把T替换为d o u b l e或l o n g，编译器又可以构造出函数 A b c的双精度型版本和长整型版本。把函数 Abc 编写成模板函数可以让我们不必了解形式参数的数据类型。

1.2.3 引用参数

程序1 - 3中形式参数的用法会增加程序的运行开销。例如，我们来考察一下函数被调用以及返回时所涉及的操作。假定a，b 和c 是传值参数，在函数被调用时，类型T 的复制构造函数把相应的实际参数分别复制到形式参数a，b 和c 之中，以供函数使用；而在函数返回时，类型

T的析构函数会被唤醒，以便释放形式参数a，b 和c。

假定数据类型为用户自定义的 M a t r i x，那么它的复制构造函数将负责复制其所有元素，而析构函数则负责逐个释放每个元素（假定 Matrix 已经定义了操作符+，*和 /）。如果我们用具有1 0 0 0个元素的Matrix 作为实际参数来调用函数 A b c，那么复制三个实际参数给 a，b 和c 将需要3 0 0 0次操作。当函数 A b c返回时，其析构函数又需要花费额外的 3 0 0 0次操作来释放 a， b和c。

在程序 1 - 4所示的代码中， a，b 和c 是引用参数（ reference parameter）。如果用语句 A bc (x,y, z) 来调用函数A b c，其中x、y 和z 是相同的数据类型，那么这些实际参数将被分别赋予名称a，b 和c，因此，在函数Abc 执行期间，x、y 和z 被用来替换对应的a，b 和c。与传值参数的情况不同，在函数被调用时，本程序并没有复制实际参数的值，在函数返回时也没有调用析构函数。

程序1-4 利用引用参数计算一个表达式

template<class T>

T Abc(T& a, T& b, T& c)

{

return a+b+b*c+(a+b-c)/(a+b)+4;

}

我们可以考察一下当a，b 和c 所对应的实际参数x，y 和z 分别是具有 0 0 0个元素的矩阵时的情形。由于不需要把x，y 和z 的值复制给对应的形式参数，因此我们可以节省采用传值参数进行参数复制时所需要的3 0 0 0次操作。

1.2.4 常量引用参数

C + +还提供了另外一种参数传递方式——常量引用（ const reference），这种模式指出函数不得修改引用参数。例如，在程序 1 - 4中，a，b 和c 的值不能被修改，因此我们可以重写这段代码，见程序1 - 5。

程序1-5 利用常量引用参数计算一个表达式

template<class T>

T Abc(const T& a, const T& b, const T& c)

{

return a+b+b*c+(a+b-c)/(a+b)+4;

}

使用关键字const 来指明函数不可以修改引用参数的值，这在软件工程方面具有重要的意义。这将立即告诉用户该函数并不会修改实际参数。

对于诸如i n t、float 和char 的简单数据类型，当函数不会修改实际参数值的时候我们可以采用传值参数；对于所有其他的数据类型（包括模板类型），当函数不会修改实际参数值的时候可以采用常量引用参数。

采用程序1 - 6的语法，我们可以得到程序 1 - 5的一个更通用的版本。在新的版本中，每个形式参数可能属于不同的数据类型，函数返回值的类型与第一个参数的类型相同。

程序1-6 程序1 - 5的一个更通用的版本

template<class Ta, class Tb, class Tc >

Ta Abc (const Ta& a, const Tb& b, const Tc& c)

{

return a+b+b*c+(a+b-c)/(a+b)+4;

}

将被释放，其值当然也不再有效。为了避免丢失这个值，在释放临时变量以及传值形式参数的空间之前，必须把这个值从临时变量复制到调用该函数的环境中去。如果需要返回一个引用，可以为返回类型添加一个前缀 &。如：

T& X(int i, T& z)

定义了一个函数X，它返回一个引用参数Z。可以使用下面的语句返回z：

return z；

这种返回形式不会把z 的值复制到返回环境中。当函数X返回时，传值形式参数i 以及所有局部变量所占用的空间都将被释放。由于z 是对一个实际参数的引用，因此，它不会受影响。

如果在函数名之前添加关键字c o n s t，那么函数将返回一个常量引用，例如：

const T& X (int i, T& z)

除了返回的结果是一个不变化的对象之外，返回一个常量引用与返回一个引用是相同的。

1.2.6 递归函数

递归函数（recursive function）是一个自己调用自己的函数。递归函数包括两种：直接递归（direct recursion）和间接递归（indirect recursion）。直接递归是指函数F的代码中直接包含了调用F的语句，而间接递归是指函数F调用了函数G，G又调用了H，如此进行下去，直到F又被调用。在深入探讨C + +递归函数之前，我们来考察一下来自数学的两个相关概念——数学函数的递归定义以及归纳证明。

在数学中经常用一个函数本身来定义该函数。例如阶乘函数 f (n) =n！的定义如下：

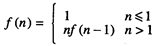        （1 - 1）

其中n 为整数。

从该定义中可以看到，当n 小于或等于1时，f (n)的值为1，如 f (-3) = f (0) = f (1) =1。当n 大于1时，f (n)由递归形式来定义，在定义的右侧也出现了 f 。在右侧使用f 并不会导致循环定义，因为右侧f 的参数小于左侧f 的参数。例如，从公式（1 - 1）中可以得到f ( 2 ) = 2f ( 1 )，由于我们已经知道f ( 1 ) = 1，因此 f ( 2 ) = 2 * 1 = 2。以此类推，f ( 3 ) = 3f ( 2 ) = 3 * 2 = 6。

对于函数f (n) 的一个递归定义（假定是直接递归），要想使它成为一个完整的定义，必须满足如下条件：

• 定义中必须包含一个基本部分（ b a s e），其中对于n 的一个或多个值，f (n)必须是直接定义的（即非递归）。为简单起见，我们假定基本部分包含了n≤ k 的情况，其中k 为常数。（在基本部分中指定n≥ k 的情形也是可能的，但较少见。）
• 在递归部分（recursive component）中，右侧所出现的所有f 的参数都必须有一个比n 小，以便重复运用递归部分来改变右侧出现的f ，直至出现f 的基本部分。

在公式（1 - 1）中，基本部分是：当n≤ 1时f (n) = 1；递归部分是f (n) = nf (n- 1 )，其中右侧f 的参数为n- 1，比n 要小。重复应用递归部分可把f (n- 1 )变换成对f (n- 2 )，f (n- 3 )，⋯ ，直到f ( 1 ) 的调用。例如：

f (5) = 5f (4) = 20f (3) = 60f (2) = 120f ( 1 )

注意每次应用递归部分的结果是更趋近于基本部分，最后，根据基本部分的定义可以得到 f (5) = 120。从这个例子中可以看出，对于n≥ 1有 f (n) = n (n-1) (n- 2 )⋯ 1。

作为递归定义的另外一个例子，我们来考察一下斐波那契数列的定义：

F0 = 0，F1 = 1，Fn =Fn - 1+Fn -2 （n> 1） （1 - 2）在这个定义中，F₀ = 0和F₁ =1 构成了定义的基本部分，F_n =F_{n - 1}+F_{n -2} 是定义的递归部分。右侧函数的参数都小于 n。为使公式（1 - 2）成为F 的一个完整的递归定义，对于任何 n> 1的斐波那契数，对递归部分的重复应用应能把右侧出现的所有 F 变换成基本部分的形式。因为对一个 n> 1的整数重复减去 1或2会得到0或1，因此右侧 F 的出现总可以被变换成基本定义。比如，

F =F +F =F +F +F +F = 3F + 2F = 3。

4    3    2    2     1     1     0     1     0

现在我们把注意力转向与计算机递归函数相关的第二个概念——归纳证明。在归纳证明中，可以按照如下步骤来证明一个命题的正确性，比如证明如下公式：

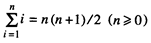        （1 - 3）

首先我们可以验证，对于n 的一个或多个基本的值（如n = 0或n = 0 , 1）该公式是成立的；然后假定当n∈ ( 0 ~m）时公式是成立的，其中m 是一个任意整数（大于等于验证时所取的最大值），如果能够证明对于n 的下一个值（如m+ 1）公式也是成立的，那么就可以确定该公式是成立的。

这种证明方法可以归纳为三个部分——归纳初值（ induction base），归纳假设（ i n d u c t i o n h y p o t h e s i s）和归纳步证明（induction step）。

下面通过对n 进行归纳来证明公式（ 1 - 3）。在归纳初值部分，取 n= 0来进行验证，由于公

式的左边 i= 0，公式的右边也为 0，所以当n= 0时公式（1 - 3）是成立的。在归纳假设部分假

i =1

定当n≤ m 时公式是成立的，其中m 是任意大于等于0的整数（对于接下来的归纳证明，只需假定n = m 时公式是成立的即可）。在归纳证明中需要证明当n =m +1 时公式（1 - 3）是成立的。对

于n=m+ 1，公式左边为 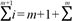i，从归纳假设中可以知道 i=m (m+ 1 ) / 2，所以当n =m + 1

    i =1    i =1    t=1

时左边变成m+ 1 +m (m+1)/2 =(m+1) (m+ 2 ) / 2，正好与公式右边相等。

乍看起来，归纳证明好象是一个循环证明——因为我们建立了一个假设为正确的结论。不过，归纳证明并不是循环证明，就像递归定义并不是循环定义一样。每个正确的归纳证明都会有一个基本值验证部分，它与递归定义的基本部分相类似，在归纳证明时我们利用了比 n 值小时结论的正确性来证明取值为n 时结论的正确性。重复应用归纳证明，可以减少对基本值验证的应用。

C + +允许我们编写递归函数。一个正确的递归函数必须包含一个基本部分。函数中递归调用部分所使用的参数值应比函数的参数值要小，以便函数的重复调用能最终获得基本部分所提供的值。

例1-1 [阶乘] 程序1 - 7给出了一个利用公式（1 - 1）计算n! 的C + +函数。函数的基本部分包含了

n≤ 1的情形。考虑调用F a c t o r i a l ( 2 )。为了计算e l s e语句中的2* Factorial(1)，需要挂起F a c t o r i a l ( 2 )，然后进入调用F a c t o r i a l ( 1 )。当Factorial(2) 被挂起时，程序的状态（如局部变量、传值形式参数的值、引用形式参数的值以及代码的执行位置等）被保留在递归栈中，在执行完 F a c t o r i a l ( 1 )时这些程序状态又立即恢复。调用Factorial(1) 所得到的返回值为1，之后，F a c t o r i a l ( 2 )恢复运行，计算表达式2 * 1，并将结果返回。

程序1-7 计算n！的递归函数

int Factorial (int n)

{ / /计算n！

if (n<=1) return 1; else return n * Factorial(n-1 ) ;

}

在计算F a c t o r i a l ( 3 )时，当到达e l s e语句时，计算过程被挂起以便先计算出 F a c t o r i a l ( 2 )。我

们已经看到F a c t o r i a l ( 2 )是怎样获得最终结果2的。当F a c t o r i a l ( 2 )返回时，F a c t o r i a l ( 3 )继续运行，计算出最后的结果3 * 2。

鉴于程序1 - 7的代码与公式（1 - 1）的相似性，该程序的正确性与公式（ 1 - 1）的正确性是等

价的。

例1-2 模板函数S u m (见程序1-8) 统计元素a [ 0 ]至a[n-1] 的和（简记为a [ 0 : n - 1 ]）。从代码中我们可以得到这样的递归公式：当 n = 0时，和为0；当n > 0时，n个元素的和是前面n - 1个元素的和加上最后一个元素。见程序1 - 9。

程序1-8 累加a [ 0：n - 1 ]

template<class T> T Sum(T a[], int n)

{ / /计算a[0: n-1]的和 T tsum=0;

f or    (int i = 0; i < n; i++) tsum += a[i];

return tsum;

}

程序1-9 递归计算a [ 0：n - 1 ]

template<class T> T Rsum(T a[], int n)

{ / /计算a[0: n-1]的和 if (n > 0) return Rsum(a, n-1) + a[n-1];

return 0;

}

例1-3 [排列] 通常我们希望检查n 个不同元素的所有排列方式以确定一个最佳的排列。比如， a，b 和c 的排列方式有：a b c, a c b, b a c, b c a, cab 和c b a。n 个元素的排列方式共有 n ！种。

由于采用非递归的C + +函数来输出n 个元素的所有排列方式很困难，所以可以开发一个递归函数来实现。令E= {e , ..., e }表示n 个元素的集合，我们的目标是生成该集合的所有排列方 1     n

式。令E_i 为E中移去元素i 以后所获得的集合，perm (X) 表示集合X 中元素的排列方式，e_i . p e r m

(X)表示在 perm (X) 中的每个排列方式的前面均加上 e_i 以后所得到的排列方式。例如，如果

E= {a, b, c}，那么E₁= {b, c}，perm (E₁ ) = (b c, c b)，e₁ .perm (E₁) = (a b c, a c b)。

对于递归的基本部分，采用 n = 1。当只有一个元素时，只可能产生一种排列方式，所以

perm (E) = (e)，其中 e 是E 中的唯一元素。当 n > 1时，perm (E) = e .perm (E ) +e .p e r m

    1     1     2

(E₂ ) +e₃.perm (E₃) + ⋯ +e_n .perm (E_n )。这种递归定义形式是采用n 个perm (X) 来定义perm (E), 其中每个X 包含n- 1个元素。至此，一个完整的递归定义所需要的基本部分和递归部分都已完成。当n= 3并且E=（a, b, c）时，按照前面的递归定义可得perm (E) =a.perm ( {b, c} ) +b.perm ( {a,

c} ) +c.perm ( {a, b} )。同样，按照递归定义有 perm ( {b, c} ) =b.perm ( {c} ) +c.perm ( {b}), 所以 a.perm ( {b, c} ) = ab.perm ( {c} ) + ac.perm ( {b}) = a b . c + ac.b = (a b c, a c b)。同理可得

b.perm ( {a, c}) = ba.perm ( {c}) + bc.perm ( {a}) = b a . c + b c . a = (b a c, b c a)，c.perm ( {a, b}) = ca.perm ( {b}) + cb.perm ( {a}) = c a . b + c b . a = (c a b, c b a)。所以perm (E) = (a b c, a c b, b a c, b c a, c a b, c b a)。

注意a.perm ( {b, c} )实际上包含两个排列方式：abc 和a c b，a 是它们的前缀，perm ( {b, c} )

是它们的后缀。同样地，ac.perm ( {b}) 表示前缀为a c、后缀为perm ( {b}) 的排列方式。

程序1 - 1 0把上述perm (E) 的递归定义转变成一个C++ 函数，这段代码输出所有前缀为l i s t [ 0：

k-1], 后缀为l i s t [ k：m] 的排列方式。调用Perm(list, 0, n-1) 将得到list[0: n-1] 的所有n! 个排列方式，在该调用中，k=0, m= n - 1，因此排列方式的前缀为空，后缀为list[0: n-1] 产生的所有排列方式。当k =m 时，仅有一个后缀l i s t [ m ]，因此list[0: m] 即是所要产生的输出。当k<m时，先用list[k] 与l i s t [ k：m] 中的每个元素进行交换，然后产生list[k+1: m] 的所有排列方式，并用它作为list[0: k] 的后缀。S w a p是一个inline 函数，它被用来交换两个变量的值，其定义见程序 1 11。P e r m的正确性可用归纳法来证明。

程序1-10 使用递归函数生成排列

template<class T>

void Perm(T list[], int k, int m)

{ / /生成list [k：m ]的所有排列方式 int i;

if (k == m) {//输出一个排列方式

for (i = 0; i <= m; i++)

cout << list [i];

cout << endl;

}

else // list[k：m ]有多个排列方式

// 递归地产生这些排列方式 for (i=k; i <= m; i++) {

Swap (list[k], list[i]);

Perm (list, k+1, m);

Swap (list [k], list [i]);

}

}

程序1 - 11 交换两个值

template <class T> inline void Swap(T& a, T& b)

{// 交换a和b

T temp = a; a = b; b = temp;

}

练习

1. 试编写一个模板函数I n p u t，它要求用户输入一个非负数，并负责验证用户所输入的数是否真的大于或等于0，如果不是，它将告诉用户该输入非法，需要重新输入一个数。在函数非成功退出之前，应给用户三次机会。如果输入成功，函数应当把所输入的数作为引用参数返回。

输入成功时，函数应返回true, 否则返回f a l s e。上机测试该函数。

1. 试编写一个模板函数，用来测试数组a中的元素是否按升序排列（即a [ i ]≤ a [ i + 1 ] ,其中0≤ i＜n - 1）。如果不是，函数应返回f a l s e，否则应返回t r u e。上机测试该函数。
2. 试编写一个非递归函数来计算n！，并上机测试函数的正确性。
3. 1) 试编写一个计算斐波那契数列F 的递归函数，并上机测试其正确性。

   n

1. 试说明对于任何n>2 的整数，调用1）中的函数计算 F_n 时，同一个 F_i 会被处理至少一次。
2. 试编写一个非递归的函数来计算斐波那契数列 F_n ，该函数应能直接计算出每个斐波那契数。上机测试代码的正确性。
   1. 试编写一个递归函数，用来输出n 个元素的所有子集。例如，三个元素{a, b, c} 的所有子集是：{ }（空集），{a}, {b}, {c}, {a, b}, {a, c}, {b, c} 和{a, b, c}。
   2. 试编写一个递归函数来确定元素x 是否属于数组a[ 0：n- 1 ]。

1.3 动态存储分配

1.3.1 操作符n e w

C + +操作符n e w可用来进行动态存储分配，该操作符返回一个指向所分配空间的指针。例如，为了给一个整数动态分配存储空间，可以使用下面的语句来说明一个整型指针变量：

int *y；

当程序需要使用该整数时，可以使用如下语法来为它分配存储空间：

y = new int;

操作符n e w分配了一块能存储一个整数的空间，并将指向该空间的指针返回给 y，y是对整数指针的引用，而* y则是对整数本身的引用。为了在刚分配的空间中存储一个整数值，比如 1 0，可以使用如下语法：

*y = 10;

我们可以把上述三步（说明y, 分配存储空间，为*y 赋值）进行适当的合并，如下例所示：

int *y = new int;

*y = 10; 或

int *y = new int (10); 或

int *y;

y = new int (10);

1.3.2 一维数组

在本书的许多示例程序中都使用了一维或二维数组，这些数组的大小在编译时可能是未知的，事实上，它们可能随着函数调用的变化而变化。因此，对于这些数组必须进行动态存储分配。

为了在运行时创建一个一维浮点数组 x，首先必须把x说明成一个指向f l o a t的指针，然后为数组分配足够的空间。例如，一个大小为n 的一维浮点数组可以按如下方式来创建：

float *x = new float [n];

 

操作符n e w分配n 个浮点数所需要的空间，并返回指向第一个浮点数的指针。可以使用如下语法来访问每个数组元素：x[0], x[1], ..., x[n-1]。

1.3.3 异常处理

在执行语句

float *x = new float [n];

时，如果计算机不能分配足够的空间怎么办？在这种情况下， new 不能够分配所需数量的存储空间，将会引发一个异常（e x c e p t i o n）。在Borland C++中，当new 不能分配足够的空间时，它会引发（t h r o w）一个异常xalloc (在except.h 中定义)。可以采用try - catch 结构来捕获（c a t c h） new 所引发的异常：

float *x;

try {x = new float [n];}

catch (xalloc) { // 仅当new 失败时才会进入 cerr << "Out of Memory" << endl; e x i t ( 1 ) ; }

当一个异常出现时，程序进入与该异常相对应的c a t c h语句块中执行。在上面的例子中，只有在执行try 语句时产生了xalloc 异常，才会进入catch (xalloc) 语句块，由语句exit (1) 终止程序的运行。（exit () 在stdlib.h 中定义。）

在C++ 程序中处理错误条件的常用方法就是每当检测到这样的条件时就引发一个异常。当一个异常被引发时，必须指明它的类型（如前面的 x a l l o c）。我们把可能会产生异常的程序代码放入try 块中，在try 块之后放上一个或多个catch 块，每个catch 块用来处理一个特定类型的异常。例如catch (xalloc) 块仅处理xalloc 异常。语法catch (...) 定义了一个能捕获所有异常的c a t c h 块。当一个异常被引发时，检查在程序执行过程中所遇到的最接近的 try-catch 代码，如果其中的一个catch 块能够处理所产生的异常，程序将从这个catch 块中继续执行，否则，继续检查直到找到与异常相匹配的块。如果找不到能处理该异常的 c a t c h块，程序将显示信息" A b n o r m a l program termination（异常程序终结）" 并终止运行。如果一个try 块没有引发异常，程序的执行将越过与该t r y块相对应的c a t c h块。

1.3.4 操作符d e l e t e

动态分配的存储空间不再需要时应该被释放，所释放的空间可重新用来动态创建新的结构。

可以使用C + +操作符d e l e t e来释放由操作符n e w所分配的空间。下面的语句可以释放分配给 * y的空间以及一维数组x：

delete y;

delete [ ] x;

1.3.5 二维数组

虽然C + +提供了多种机制用来说明二维数组，但其中的多数机制都要求在编译时明确地知道每一维的大小。而且，在使用这些机制时，很难编写出一个允许形式参数是一个第二维大小未知的二维数组的函数。之所以如此，是因为当形式参数是一个二维数组时，必须指定其第二维的大小。例如，a[ ][10]是一个合法的形式参数，而a[ ][ ] 不是。

克服这种限制的一条有效途径就是对于所有的二维数组使用动态存储分配。本书从头至尾使用的都是动态分配的二维数组。

当一个二维数组每一维的大小在编译时都是已知时，可以采用类似于创建一维数组的语法来创建二维数组。例如，一个类型为c h a r的7× 5数组可用如下语法来定义：

char c[7][5];

如果在编译时至少有一维是未知的，必须在运行时使用操作符 n e w来创建该数组。一个二维字符型数组，假定在编译时已知其列数为5，可采用如下语法来分配存储空间：

char (*c)[5];

try { c = new char [n][5];}

catch (xalloc) {//仅当n e w失败时才会进入 cerr << "Out of Memory" << endl; exit (1);}

在运行时，数组的行数 n要么通过计算来确定，要么由用户来指定。如果在编译时数组的列数也是未知的，那么不可能调用一次 n e w就能创建该数组（即使数组的行数是已知的）。构造二维数组时，可以把它看成是由若干行组合起来的，每一行都是一个一维数组，可以按照前面讨论的方式用n e w来创建，指向每一行的指针可以保存在另外一个一维数组之中。图 1 - 1给出了建立一个3× 5数组所需要的结构。

x[0], x[1], x[2]分别指向第0行，第1行和第2行的第一个元素。所以，如果x是一个字符数组，那么x [ 0 : 2 ]是指向字符的指针，而x本身是一个指向指针的指针。可用如下语法来说明 x :

char **x;

为了创建如图1 - 1所示的存储结构，可以使用程序 1 - 1 2中的代码，该程序创建一个类型为 T 的二维数组，这个数组有r o w s行和c o l s列。程序首先为指针x [ 0 ] , . . . , x [ r o w s - 1 ]申请空间，然后为数组的每一行申请空间。在程序中操作符 n e w被调用了r o w s + 1次。如果n e w的某一次调用引发了一个异常，程序控制将转移到c a t c h块中，并返回f a l s e。如果没有出现异常，数组将被成功创建，函数M a k e 2 D A r r a y返回t r u e。对于所创建的数组x中的元素，可以使用标准的用法来引用，如x [ i ] [ j ] ,其中0≤ i＜r o w s , 0≤ j＜c o l s。

图1-1 一个3× 5数组的存储结构

程序1-12 为一个二维数组分配存储空间

template <class T> bool Make2DArray ( T ** &x, int rows, int cols)

{// 创建一个二维数组

t r y {

/ /创建行指针

x = new T * [rows];

/ /为每一行分配空间

for (int i = 0 ; i < rows; i++) x[i] = new int [cols];

return true;

}

catch (xalloc) {return false;}

}

在程序1 - 1 2中，函数通过返回布尔值false 把n e w所产生的异常（如果有的话）告诉调用者。当然，M a k e 2 D A r r a y失败时也可以什么都不做，这样也能使调用者知道产生了异常。如果使用程序1 - 1 3中的代码，调用者可以捕获由n e w所产生的任何异常。

程序1-13 创建一个二维数组但不处理异常

template <class T> void Make2DArray( T ** &x, int rows, int cols)

{// 创建一个二维数组

// 不捕获异常

/ /创建行指针

x = new T * [rows];

/ /为每一行分配空间

for (int i = 0 ; i<rows; i++) x[i] = new int [cols];

}

当M a k e 2 D A r r a y按程序1 - 1 3定义时，可以使用如下代码来确定存储分配是否成功：

try { Make2DArray (x, r, c);} catch (xalloc) {cerr<< "Could bot create x" << endl; e x i t ( 1 ) ; }

在M a k e 2 D A r r a y中不捕获异常不仅简化了函数的代码设计，而且可以使用户在一个更合适的地方捕获异常，以便更好地报告出错误的明确含义或进行错误恢复。

可以按如下两步来释放程序1 - 1 2中为二维数组所分配的空间。首先释放在 f o r循环中为每一

行所分配的空间，然后释放为行指针所分配的空间，具体实现见程序 1 - 1 4。注意在程序1 - 1 4中 x被置为0，以便阻止用户继续访问已被释放的空间。

程序1-14 释放由M a k e 2 D A r r a y所分配的空间

template <class T> void Delete2DArray( T ** &x, int rows)

{// 删除二维数组x

/ /释放为每一行所分配的空间 for (int i = 0 ; i < rows ; i++)

delete [ ] x[i];

/ /删除行指针

delete [] x; x = 0;

}

练习

1. 假定用一维数组 a [ 0：s i z e - 1 ]来存储一组元素。如果有 n个元素，可以把它们存储在 a [ 0 ] , . . . , a [ n - 1 ]中。当n超过s i z e时，数组将不足以存储所有元素，必须分配一个更大的数组。类似地，如果元素的数目比 s i z e小很多，我们又可能希望减少数组的大小，以便释放出多余的空间为其他地方所用。试编写一个模板函数 C h a n g e S i z e 1 D把数组a的大小从s i z e变成To S i z e。函数首先应该分配一个新的、大小为 To S i z e的数组，然后把原数组a中的n个元素复制到新数组a中，最后释放原数组a所占用的空间。上机测试该函数。
2. 试编写一个函数ChangeSize2D 来改变一个二维数组的大小（见练习7）。上机测试该函数。

1.4 类

1.4.1 类C u r r e n c y

C + +语言支持诸如 i n t , f l o a t和c h a r之类的数据类型，在本书所提供的许多应用中还使用了

C + +语言不直接支持的数据类型。用C + +来定义自有数据类型最灵活的方式就是使用类（ c l a s s）结构。假定你想处理类型 C u r r e n c y的对象，其实例拥有三个成员：符号（＋或－），美元和美分。举两个例子，如$2.35 (符号是＋，2美元，3 5美分)和- $ 6 . 0 5 (符号是－，6美元，5美分)。对这种类型的对象我们想要执行的操作如下：

1. 设置成员的值。
2. 确定各成员的值（如指出符号，美元数目和美分数目）。
3. 增加两种货币类型。
4. 增加成员的值。
5. 输出。

假定用无符号长整型变量d o l l a r s、无符号整型变量c e n t s和s i g n类型的变量s g n来描述货币对象，其中s i g n类型的定义如下：

enum sign { plus, minus};

可以使用程序1 - 1 5中的语法来定义C + +类C u r r e n c y。第一行简单地说明一个名为C u r r e n c y的类，然后在一对括号（{ }）之间给出类描述。类描述被分成两个部分： public 和p r i v a t e。public 部分用于定义一些函数（又称方法），这些函数可对C u r r e n c y类对象（或实例）进行操作，它们对于C u r r e n c y类的用户是可见的，是用户与 C u r r e n c y对象进行交互的唯一手段。 p r i v a t e部分用于定义函数和数据成员（如简单变量，数组及其他可赋值的结构），这些函数和数据成员对于用户来说是不可见的。借助于 p u b l i c部分和p r i v a t e部分，我们可以使用户只看到他（或她）需要看到的部分，同时把其余信息隐藏起来。尽管 C + +语法允许在p u b l i c部分定义数据成员，但在软件工程实践中不鼓励这种做法。

程序1-15 定义C u r r e n c y类

class Currency { p u b l i c :

// 构造函数

Currency(sign s = plus, unsigned long d = 0, unsigned int c = 0);

// 析构函数

~Currency() {} bool Set(sign s, unsigned long d, unsigned int c); bool Set(float a); sign Sign() const {return sgn;} unsigned long Dollars() const {return dollars;} unsigned int Cents() const {return cents;} Currency Add(const Currency& x) const; Currency& Increment(const Currency& x); void Output() const; p r i v a t e :

sign sgn; unsigned long dollars; unsigned int cents;

} ;

p u b l i c部分的第一个函数与 C u r r e n c y类同名，这种函数称之为构造函数。构造函数指明如何创建一个给定类型的对象，它不可以有返回值。在本例中，构造函数有三个参数，其缺省值

分别是plus, 0和0，构造函数的具体实现在本节稍后给出。在创建一个 C u r r e n c y类对象时，构造函数被自动唤醒。可以采用如下两种方式来创建 C u r r e n c y类对象：

Currency f, g (plus, 3,45), h (minus, 10);

Currency *m = new Currency ( plus, 8, 12);

第一行定义了三个C u r r e n c y类变量（f，g 和h），其中f 被初始化为缺省值plus, 0和0，而g被初始化为$ 3 . 4 5，h 被初始化为－$ 1 0 . 0 0。注意初始值从左至右分别对应构造函数的每个参数。如果初始值的个数少于构造函数参数的个数，剩下的参数将取缺省值。在第二行， m被定义为指向一个C u r r e n c y对象的指针。我们调用 n e w函数来创建一个C u r r e n c y对象，并把对象的指针存储在m中。所创建的对象被初始化为$ 8 . 1 2。

下一个函数为~ C u r r e n c y，与类名相比多了一个前缀（ ~），这个函数被称为析构函数。每当一个C u r r e n c y对象超出作用域时将自动调用析构函数。这个函数用来删除对象。在本例中析构函数被定义为空函数（ { }）。对于其他类，由于类的构造函数可能会创建一些动态数组，那么当对象超出作用域时，析构函数需要释放这些空间。与构造函数一样，析构函数也不可以有返回值。

接下来的两个函数允许用户为 C u r r e n c y类成员赋值。其中第一个函数要求用户提供三个参

数，而第二个函数需要一个浮点数作为参数。如果成功，两个函数均返回 true, 否则返回f a l s e。这两个函数的具体实现在本节稍后给出。请注意，这两个函数具有相同的名字，但编译器和用户都很容易区分它们，因为它们具有不同的参数集合。 C + +允许函数名的重用，只要它们的参数表不同。还需要注意的是，没有指定欲赋值（符号，美元，美分）对象的名称，这是因为调用类成员函数的语法如下：

g . S e t ( m i n u s , 3 3 , 0 ) ; h . S e t ( 2 0 . 5 2 ) ;

其中g 和h 是Currency 类变量。在第一个句子中，g 是唤醒Set 的对象，而在第二个句子中h是唤醒Set 的对象。在为函数S e t编写代码时，我们有办法访问调用本函数的对象，因此，不需要把对象的名称放入参数表中。

函数S i g n，D o l l a r s和C e n t s返回对象的相应数据成员，关键字 c o n s t指出这些函数不会修改数据成员。我们把这种类型的函数称之为常元函数（ constant function）。

函数S u m把当前对象的货币数量与对象x的货币数量相加，然后返回所得结果，因此A d d函数不会修改当前对象，是一个常元函数。函数 I n c r e m e n t把对象x 的货币数量添加到当前对象上，这个函数修改了当前对象，因此不是一个常元函数。最后一个函数是 O u t p u t，它显示当前对象的货币数量。函数Output 不会修改当前对象，因此是一个常元函数。

尽管A d d和I n c r e m e n t都返回C u r r e n c y类对象，但A d d返回的是值，而I n c r e m e n t返回的是引用。如1 . 2 . 5节所提到的，返回值和返回引用分别与传值参数和引用参数有相同的作用。在返回一个值的情况下，返回的对象被复制到所返回的环境，而返回引用则避免了这种复制，在返回的环境中可以直接使用该对象。返回引用比返回值要快，因为省去了复制过程。从 A d d的代码中可以看出，它返回了一个局部对象，在函数终止时该对象将被删除，因此， r e t u r n语句必须复制该对象。而I n c r e m e n t返回的是一个全局对象，因而不需要复制。

复制构造函数被用来执行返回值的复制及传值参数的复制。程序 1 - 1 5中没有给出复制构造函数，所以C + +将使用缺省的复制构造函数，它仅可进行数据成员的复制。对于类 C u r r e n c y来说，使用省缺的复制构造函数已经足够。后面还将看到许多类，对于这些类缺省的复制构造函数已难以胜任它们的复制工作。

在p r i v a t e部分，定义了三个数据成员，它们对于一个 C u r r e n c y对象来说是必须的。每一个

C u r r e n c y对象都拥有自己的这三个数据成员。

由于在类定义的内部没有给出函数的具体实现，因此必须在其他地方给出。在具体实现时，必须在每个函数名的前面加上 C u r r e n c y：：，以指明该函数是 C u r r e n c y类的成员函数。所以

C u r r e n c y：：C u r r e n c y表示该函数是C u r r e n c y类的构造函数，而C u r r e n c y：：O u t p u t表示该函数是

C u r r e n c y类的O u t p u t函数。程序1 - 1 6给出了C u r r e n c y类的构造函数。

程序1-16 Currency类的构造函数

Currency::Currency(sign s, unsigned long d, unsigned int c)

{// 创建一个C u r r e n c y对象

if(c > 99)

{ / /美分数目过多

cerr << "Cents should be < 100" << endl; e x i t ( 1 ) ; }

sgn = s; dollars = d; cents = c;

}

构造函数在初始化当前对象的 sgn, dollars 和cents 数据成员之前需要验证参数的合法性。如果参数值出现错误，构造函数将输出一个错误信息，然后调用函数 e x i t ( )终止程序的运行。在本例中，仅需要验证c 的值。

程序1 - 1 7给出了两个S e t函数的代码。第一个函数首先验证参数的合法性，如果参数合法，则用它们来设置p r i v a t e成员变量。第二个函数不执行参数合法性验证，它仅使用小数点后面的

头两个数字。形如 d₁.d₂d₃ 的数可能没有一个精确的计算机表示，例如，用计算机所描述的数

5 . 2 9实际上要比真正的5 . 2 9稍微小一点。当用如下语句

cents = (a - dollars) * 100

抽取cents 成员时，这种描述方法可能会带来一个错误，因为 (a - dollars) * 100稍微小于2 9，当程序把(a - dollars) * 100转换成一个整数时，c e n t s得到的将是2 8而不是2 9。只要d .d d 的计

    1    2    3

算机表示与实际值相比不少于 0 . 0 0 1或不多于0 . 0 0 9，就可以采用为a 加上0 . 0 0 1来解决我们的问题。例如，如果5 . 2 9的计算机表示是5 . 2 8 9 9 9，那么加上0 . 0 0 1将得到5 . 2 9 0 9 9 ,由此所计算出的 c e n t s就是2 9。

程序1-17 设置p r i v a t e数据成员

bool Currency::Set(sign s, unsigned long d, unsigned int c)

{// 取值

if (c > 99) return false; sgn = s; dollars = d; cents = c; return true;

}

bool Currency::Set(float a)

{// 取值

if (a < 0) {sgn = minus; a = -a;} else sgn = plus; dollars = a; // 抽取整数部分

// 获取两个小数位

cents = (a + 0.005 - dollars) * 100; return true;

}

程序1 - 1 8给出了函数 A d d的代码，该函数首先把要累加的两个货币数量转换成整数，如 $2.32 变成整数2 3 2，－$ 4 . 7 5变成整数－4 7 5。请注意引用当前对象的数据成员与引用参数 x的数据成员在语法上有所区别。 x . d o l l a r s指定x 的数据成员dollars ，而当前对象使用d o l l a r s时可以直接引用d o l l a r s而不必在它的前面加上对象名。当函数 A d d终止时，局部变量 a 1 , a 2 , a 3和a n s 被l o n g数据类型的析构函数删除，这些变量所占用的空间也将被释放。由于 C u r r e n c y对象a n s将被作为调用结果返回，因此必须把它复制到调用者的环境中，所以 A d d返回的是值。

程序1-18 累加两个C u r r e n c y

Currency Currency::Add(const Currency& x) const {// 把 x累加到 * t h i s . long a1, a2, a3;

Currency ans;

// 把当前对象转换成带符号的整数 a1 = dollars * 100 + cents; if (sgn == minus) a1 = -a1;

// 把x转换成带符号的整数

a2 = x.dollars * 100 + x.cents; if (x.sgn == minus) a2 = －a 2 ;

a3 = a1 + a2;

// 转换成 currency 形式

if (a3 < 0) {ans.sgn = minus; a3 = －a 3 ; } else ans.sgn = plus; ans.dollars = a3 / 100;

ans.cents = a3 - ans.dollars * 100;

return ans;

}

程序1 - 1 9给出了函数I n c r e m e n t和O u t p u t的代码。在C + +中，保留关键字t h i s用于指向当前对

象，*this 代表对象本身。看一下调用g . I n c r e m e n t ( h )。函数I n c r e m e n t的第一行调用了p u b l i c成员

函数A d d，它把x (这里是h) 加到当前对象上（这里是 g），所得结果被返回，并被赋给 * t h i s，

* t h i s就是当前对象。由于该对象不是函数I n c r e m e n t的局部对象，因此当函数结束时，该对象不会自动被删除。所以可以返回一个引用。

程序1-19 Increment与O u t p u t

Currency& Currency::Increment(const Currency& x) {// 增加量 x .

*this = Add(x); return *this;

}

void Currency::Output () const

{// 输出currency 的值

if (sgn == minus) cout << '-'; cout << '$' << dollars << '.'; if (cents < 10) cout << "0"; cout << cents;

}

通过把C u r r e n c y类的成员变成私有（p r i v a t e）,我们可以拒绝用户访问这些成员，所以用户不能使用如下的语句来改变这些成员的值：

h.cents = 20;

h.dollars = 100;

h.sgn = plus;

利用成员函数来设置数据成员的值可以确保数据成员拥有合法的值。构造函数和    S e t函数已经做到了这一点，其他函数当然也应该保证数据成员的合法性。因此，在诸如 A d d和O u t p u t 函数的代码中不必验证c e n t s是否介于0到1 0 0之间。如果数据成员被声明为 p u b l i c成员，它们的合法性将难以保证。用户可能会错误地把 c e n t s设置成3 0 5，因而将导致一些函数（如 O u t p u t函数）产生错误结果，所以，所有的函数在处理任务之前都必须验证数据的合法性。这种验证将会降低代码的执行速度，同时也使代码不够优雅。程序1 - 2 0给出了类C u r r e n c y的应用示例。这段代码假定类定义及实现都在文件 c u r r 1 . h之中。

我们一般把类定义和类实现分放在不同的文件中，然而，这种分开放置的方法可能会对后续章节中大量使用模板函数和模板类带来困难。

函数m a i n的第一行定义了四个C u r r e n c y类变量：g, h, i 和j。除h 具有初值$ 3 . 5 0外，构造函数把它们都初始化为$ 0 . 0 0。在接下来的两行中， g 和i 分别被设置成－$ 2 . 2 5和－$ 6 . 4 5，之后调用函数A d d把g 和h 加在一起，并把所返回的对象（值为$ 1 . 2 5）赋给j。为此，需使用缺省的赋值过程把右侧对象的各数据成员分别复制到左侧对象相应的数据成员之中，复制的结果是使 j 具有值$ 1 . 2 5，这个值在下一行被输出。

下两行语句把i 累加到h 上，并输出i的新值-$ 2 . 9 5。接下来的一行首先把 i和g加在一起，

然后返回一个临时对象（其值为- $ 5 . 2 0），此后，把h 加到这个临时对象上并返回一个新的临时对象，其值为-$ 1 . 7 0。新的临时对象被复制到 j 中，然后输出j 的值（为-$ 1 . 7 0）。注意' .' 序列的处理顺序是从左到右。

接下来的一行语句首先使用I n c r e m e n t为i累加g，它返回一个引用给i。A d d把i和h的和返回给j，最后输出j 的结果为-$ 1 . 7 0，i 的结果为-$ 5 . 2 0。

程序1-20 Currency类应用示例

#include <iostream.h> #include "curr1.h"

void main (void)

{

Currency g, h(plus, 3, 50), i, j; g.Set(minus, 2, 25); i . S e t ( - 6 . 4 5 ) ;

j = h.Add(g);

j.Output(); cout << endl; i . I n c r e m e n t ( h ) ;

i.Output(); cout << endl; j = i.Add(g).Add(h);

j.Output(); cout << endl; j = i.Increment(g).Add(h); j.Output(); cout << endl;

i.Output(); cout << endl;

}

1.4.2 使用不同的描述方法

假定已经有许多应用采用了程序 1 - 1 5中所定义的C u r r e n c y类，现在我们想要对 C u r r e n c y类的描述进行修改，使其应用频率最高的两个函数 A d d和I n c r e m e n t可以运行得更快，从而提高应用程序的执行速度。由于用户仅能通过 p u b l i c部分所提供的接口与 C u r r e n c y类进行交互，因此对p r i v a t e部分的修改并不会影响应用代码的正确性。所以可以修改 p r i v a t e部分而不会使应用发生变化。

在C u r r e n c y对象新的描述中，仅有一个私有数据成员，其类型为 l o n g。数1 3 2代表$ 1 . 3 2 , 而-2 0代表-$ 0 . 2 0。程序1-21, 1-22, 1-23中给出了C u r r e n c y类的新的描述方法以及各成员函数的具体实现。

注意，如果把新代码放在文件c u r r 1 . h中，则可以运行程序1 - 2 0中的代码而不需要做任何修改。对用户隐藏实现细节的一个重大好处在于可以用新的、更高效的描述来取代以前的描述而不需要改变应用代码。

程序1-21 Currency类的新定义

class Currency { p u b l i c :

// 构造函数

Currency(sign s = plus, unsigned long d = 0, unsigned int c = 0);

// 析构函数

~Currency() {}

bool Set(sign s, unsigned long d, unsigned int c); bool Set(float a); sign Sign() const

{if (amount < 0) return minus; else return plus;}

unsigned long Dollars() const {if (amount < 0) return (-amount) / 100; else return amount / 100;}

unsigned int Cents() const

{if (amount < 0) return -amount - Dollars() * 100;

else return amount - Dollars() * 100;}

Currency Add(const Currency& x) const;

Currency& Increment(const Currency& x)

{amount += x.amount; return *this;} void Output() const; p r i v a t e :

long amount;

} ;

程序1-22 新的构造函数及S e t函数

Currency::Currency(sign s, unsigned long d, unsigned int c)

{// 创建Currency 对象 if (c > 99)

{// 美分数目过多

cerr << "Cents should be < 100" << endl;

e x i t ( 1 ) ; }

amount = d * 100 + c; if (s == minus) amount = -amount;

}

bool Currency::Set(sign s, unsigned long d,

unsigned int c)

{// 取值

if (c > 99) return false;

amount = d * 100 + c; if (s == minus) amount = -amount; return true;

}

bool Currency::Set(float a)

{// 取值

 

sign sgn; if (a < 0) {sgn = minus; a = -a;} else sgn = plus; amount = (a + 0.001) * 100; if (sgn == minus) amount = -amount; return true;

}

程序1-23 函数A d d和O u t p u t的新代码

Currency Currency::Add(const Currency& x) const {// 把x 累加至 * t h i s .

Currency y;

y.amount = amount + x.amount; return y;

}

void Currency::Output() const

{ / /输出currency 的值 long a = amount;

if (a < 0) {cout << '-' ; a = -a;} long d = a / 100; // 美元 cout << '$' << d << '.'; int c = a-d * 100; // 美分 if (c < 10) cout << "0"; cout << c;

}

1.4.3 操作符重载

C u r r e n c y类包含了几个与 C + +标准操作符相类似的成员函数，例如， A d d进行+操作，

I n c r e m e n t进行 + =操作。直接使用这些标准的 C + +操作符比另外定义新的函数（如 A d d， I n c r e m e n t）要自然得多。可以借助于操作符重载（ operator overloading）的过程来使用+和+ =。操作符重载允许扩充现有C + +操作符的功能，以便把它们直接应用到新的数据类型或类。

程序1 - 2 4给出了把A d d和I n c r e m e n t分别替换为+和+ =的类描述。O u t p u t函数采用一个输出流的名字作为参数。这些变化仅需修改 A d d和O u t p u t的代码（见程序1 - 2 3）。程序1 - 2 5给出了修改后的代码。在这个程序还给出了重载C + +流插入操作符< <的代码。

注意在C u r r e n c y类中重载了流插入操作符，但没有定义相应的成员函数，而重载 +和+ =时则把它们定义为类成员。同样，也可以重载流抽取操作符 > >而不需要把它定义为类成员。请留意，是函数O u t p u t支持了< <的重载。由于C u r r e n c y对象的p r i v a t e成员对于非类成员函数来说不可访问（被重载的 < <不是类成员，而 +是），所以，重载 < <的代码不能引用对象 x的私有成员（在< <操作中x将被插入到输出流中）。特别地，下面的代码是错误的，因为成员 a m o u n t是不可访问的。

// 重载< < ostream& operator<< ( ostream& out, const Currency& x)

{ out << x.amount; return out; }

程序1-24 使用操作符重载的类定义

class Currency { p u b l i c :

// 构造函数

Currency(sign s = plus, unsigned long d = 0, unsigned int c = 0);

// 析构函数

~Currency() {} bool Set(sign s, unsigned long d, unsigned int c); bool Set(float a); sign Sign() const

{if (amount < 0) return minus; else return plus;}

unsigned long Dollars() const

{if (amount < 0) return (-amount) / 100; else return amount / 100;}

unsigned int Cents() const

{if (amount < 0) return -amount - Dollars() * 100;

else return amount - Dollars() * 100;}

Currency operator+(const Currency& x) const;

Currency& operator+=(const Currency& x)

{amount += x.amount; return *this;} void Output(ostream& out) const; p r i v a t e :

long amount;

} ;

程序1-25 +，O u t p u t和< <的代码

Currency Currency::operator+(const Currency& x) const {// 把 x 累加至* t h i s .

Currency y;

y.amount = amount + x.amount; return y;

}

void Currency::Output(ostream& out) const

{// 将currency 的值插入到输出流 long a = amount;

if (a < 0) {out << '-' ; a = -a ; } long d = a / 100; // 美元 out << '$' << d << '.' ; int c = a - d * 100; // 美分 if (c < 10) out << "0"; out << c;

}

// 重载< < ostream& operator<<(ostream& out, const Currency& x) {x.Output(out); return out;}

程序1 - 2 6是程序1 - 2 0的另一个版本，它假定操作符都已经被重载，程序 1 - 2 4和1 - 2 5的代码位于文件c u r r 3 . h之中。

程序1-26 操作符重载的应用

#include <iostream.h> #include "curr3.h"

void main(void)

{

Currency g, h(plus, 3, 50), i, j; g.Set(minus, 2, 25); i . S e t (-6 . 4 5 ) ;

j = h + g; cout << j << endl; i += h; cout << i << endl; j = i + g + h; cout << j << endl; j = (i+=g) + h; cout << j << endl; cout << i << endl;

}

1.4.4 引发异常

诸如构造函数和S e t函数这样的类成员在执行预定的任务时有可能会失败。在构造函数中处理错误条件的方法是退出程序，而在 S e t中则返回一个失败信号（ f a l s e）给调用者。实际上可以通过引发异常来处理这些错误，以便在程序最合适的地方捕获异常并进行处理。为了引发异常，必须首先定义一个异常类，比如B a d I n i t i a l i z e r s (见程序1 - 2 7 )。

程序1-27 异常类B a d I n i t i a l i z e r s

// 初始化失败

class BadInitializers { p u b l i c :

BadInitializers() {}

} ;

我们可以修改程序1 - 2 1中S e t函数的描述，使其返回v o i d类型。也可以修改构造函数的代码以及程序1 - 2 8中定义的第一个S e t函数的代码。其他的代码不做修改。

程序1-28 引发异常

Currency::Currency(sign s, unsigned long d, unsigned int c)

{// 创建一个C u r r e n c y对象 if (c > 99) throw BadInitializers();

amount = d * 100 + c;

if (s == minus) amount = -amount;

}

void Currency::Set(sign s, unsigned long d, unsigned int c)

{// 取值

if (c > 99) throw BadInitializers();

amount = d * 100 + c; if (s == minus) amount = -amount;

}

1.4.5 友元和保护类成员

正如前面所指出的那样，一个类的 p r i v a t e成员仅对于类的成员函数是可见的。在有些应用中，必须把对这些p r i v a t e成员的访问权授予其他的类和函数，做法是把这些类和函数定义为友元（f r i e n d）。在C u r r e n c y类例子中（见程序1 - 2 4），定义了一个成员函数O u t p u t以便于对操作符< <的重载。定义这个函数是必要的，因为如下函数：

ostream& operator <<(ostream& out, const Currency& x)

不能访问p r i v a t e成员a m o u n t。我们可以把ostream& operator<<描述为C u r r e n c y类的友元，从而避免定义附加的函数，这样就把 C u r r e n c y所有成员（包括p r i v a t e成员及p u b l i c成员）的访问权都授予了该函数。为了产生友元，需要在 C u r r e n c y类描述中引入friend 语句。为一致起见，总是把friend 语句放在类标题语句中，如：

class Currency { friend ostream& operator<< (ostream&, const Currency&); p u b l i c :

有了这个友元，就可以使用程序 1 - 2 9中的代码来重载操作符< <。当C u r r e n c y的p r i v a t e成员发生变化时，必须检查它的友元以便做出相应的变化。

程序1-29 重载友元< <

// 重载 < < ostream& operator<<(ostream& out, const Currency& x)

{// 把currency 的值插入到输出流 long a = x.amount;

if (a < 0) {out << '-' ; a = -a;} long d = a / 100; // 美元 out << '$' << d << '.' ; int c = a - d * 100; // 美分 if (c < 10) out << "0"; out << c; return out;

}

稍后我们将看到如何从一个类B派生出另外一个类A，此时类A被称为派生类（drived class），

类B被称为基类（base class）。派生类需要访问基类的部分或所有数据成员。为了便于传递这

些访问权，C + +提供了第三类成员——保护类成员（ p r o t e c t e d）。保护类成员类似于私有成员，区别在于派生类可以访问保护类成员。

用户应用程序可以访问的类成员应被声明为 p u b l i c成员，数据成员尽量不要定义为这种类型，其他成员应分成p r i v a t e和p r o t e c t e d两部分。软件工程实践告诉我们，数据成员应尽量保持为p r i v a t e成员。通过增加保护类成员来访问和修改数据成员的值，派生类可以间接访问基类的数据成员。同时，可以修改基类的实现细节而不会影响派生类。

1.4.6 增加#ifndef, #define和# e n d i f语句

文件c u r r 1 . h (或c u r r 3 . h )的全部内容包含了C u r r e n c y类的描述及实现细节。在文件头，必须放上如下语句：

#ifndef Currency_

#define Currency_

而在文件尾需要放上语句：

# e n d i f

这些语句确保C u r r e n c y的代码仅被程序包含（i n c l u d e）和编译一次。建议你为本书中所提供的其他类定义也加上相应的语句。

练习

9. 1) 采用程序1 - 1 5中的描述，所能表示的最大和最小货币值分别是多少？假定用四个字节

表示一个l o n g型数据，用两个字节表示一个i n t型数据，则一个unsigned long数介于0～2^{3 2}- 1之间，一个unsigned int数介于0～6 5 5 3 5之间。

1. 采用程序1 - 1 5中的描述，把d o l l a r s和c e n t s变成i n t型，此时所能表示的最大和最小货币值分别是多少？
2. 如果用函数A d d（见程序1 - 1 8）来累加两个货币值，为了确保从 C u r r e n c y类型转换成 long int类型时不会发生错误，a 1和a 2最大可能的值应是多少？

   10. 试扩充程序1 - 1 5中的C u r r e n c y类，为该类添加如下的p u b l i c成员函数：

   1. Input()——从标准输入流中接收一个货币值，并把它返回给调用者。
   2. Subtract(x)——从当前对象中减去对象x的值，并把结果返回。
   3. Percent(x)——返回一个C u r r e n c y对象，其值为当前对象的x %，其中, x是一个浮点数。
   4. Multiply(x)——返回一个C u r r e n c y对象，其值为当前对象乘以浮点数x。
   5. Devide(x)——返回一个C u r r e n c y对象，其值为当前对象除以浮点数x。
   1. 采用程序1 - 2 1中的描述来完成练习1 0。
   2. 1) 采用程序1 - 2 4中的描述来完成练习1 0。重载操作符> > , - , % , *和/。在重载操作符> >时，可把它定义成一个友元函数，不必专门定义一个 p u b l i c输入函数。

2) 利用重载赋值操作符 =来替换两个S e t函数。把一个整数赋值给一个 C u r r e n c y对象可用 operator=(int x) 来表示，它可用来替换第一个S e t函数，其中x表示一个包含符号、美元和美分的整数。同样，operator=(float x)可用来替换第二个S e t函数。

1.5 测试与调试

1.5.1 什么是测试

如1 . 1节所示，正确性是一个程序最重要的属性。由于采用严格的数学证明方法来证明一个程序的正确性是非常困难的（哪怕是一个很小的程序），所以我们想转而求助于程序测试

（program test）过程来实施这项工作。所谓程序测试是指在目标计算机上利用输入数据，也称之为测试数据（ test data）来实际运行该程序，把程序的实际行为与所期望的行为进行比较。如果两种行为不同，就可判定程序中有问题存在。然而，不幸的是，即使两种行为相同，也不能够断定程序就是正确的，因为对于其他的测试数据，两种行为又可能不一样。如果使用了许多组测试数据都能够看到这两种行为是一样的，我们可以增加对程序正确性的信心。通过使用所用可能的测试数据，可以验证一个程序是否正确。然而，对于大多数实际的程序，可能的测试数据的数量太大了，不可能进行穷尽测试，实际用来测试的输入数据空间的子集称之为测试集（test set）。

例1-4 [二次方程求解] 一个关于变量x 的二次函数形式如下：

a x² + b x +c

其中a, b, c 的值是已知的，且a≠ 0。3x²-2x+4, -9x²-7x, 3.5x²+ 4以及5 . 8x²+ 3 . 2x+ 5都是二次函数的实例。5x+ 3不是二次函数。

二次函数的根是指使函数的值为 0的那些x。例如，函数 f (x) =x²-5x+ 6的根为2和3，因为 f ( 2) = f (3) =0。每个二次函数都会有两个根，这两个根可用如下公式给出：

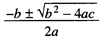
对于函数f (x) = x²-5x+6, a=1, b=-5, c= 6 ,把a, b, c 代入以上公式，可得：

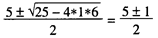
所以f (x) 的根是x = 3和x = 2。

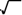
当d=b²-4ac =0 时，所得到的两个根是一样的；当 d >0 时，两个根不同且是实数；当 d <0 时，两个根也不相同且为复数，此时，每个根都有一个实部（ r e a l）和一个虚部（i m a g i n a r y）, 实部为-b/ 2a，虚部为 −d 。复数根为" 实部+虚部*i " 和" 实部－虚部*i"，其中i = −1。

函数O u t p u t R o o t s（见程序1 - 3 0）计算并输出一个二次方程的根。我们不去试图对该函数的正确性进行形式化证明，而是希望通过测试来验证其正确性。对于该程序来说，所有可能的输入数据的数目实际上就是所有不同的三元组（a, b, c）的数目，其中a≠ 0。即使a, b和c 都被限制为整数，所有可能的三元组的数目也是非常巨大，要想测试所有的三元组是不可能的。若整数的长度为1 6位，b 和c 都有2¹⁶ 种不同取值，a 有2^{1 6}-1种不同取值（因为a 不能为0），所有不同三元组的数目将达到2^{3 2}（2^{1 6}-1）。如果目标计算机能按每秒钟1 000 000个三元组的速率进行测试，那么至少需要9年才能完成！如果使用一个更快的计算机，按每秒测试 1 000 000 000 个三元组的速度，也至少需要三天才能完成。所以一个实际使用的测试集仅是整个测试数据空间中的一个子集。

程序1-30 计算并输出一个二次方程的根

template<class T> void OutputRoots(T a, T b, T c)

{// 计算并输出一个二次方程的根

T d = b*b-4 * a * c ;

if (d > 0) {// 两个实数根

float sqrtd = sqrt(d);

cout << "There are two real roots "

<< (-b+sqrtd)/(2*a) << " and "

<< (-b-sqrtd)/(2*a)

<< endl;} else if (d == 0)

// 两个根相同

cout << "There is only one distinct root "

<< -b/(2*a)

<< endl; else // 复数根

cout << "The roots are complex"

<< endl

<< "The real part is "

<< -b/(2*a) << endl

<< "The imaginary part is "

<< sqrt(-d)/(2*a) << endl;

}

如果使用数据（a, b, c）=(1, -5, 6)来进行测试，程序将输出2和3，程序的行为与期望的行为是一致的，因此可以推断对于该输入数据，程序是正确的。然而，使用一个适当的测试数据子集来验证所观察行为与所期望行为的一致性并不能证明对于所有的输入数据，程序都能够正确工作。

由于可以提供给一个程序的不同输入数据的数目一般都非常巨大，所以测试通常都被限制在一个很小的子集中进行。使用子集所完成的测试不能完全保证程序的正确性。所以，测试的目的不是去建立正确性认证，而是要暴露程序中的错误！必须选择能暴露程序中所存在错误的测试数据，不同的测试数据可以暴露程序中不同的错误。

例1-5 测试数据(a, b, c)=(1, -5, 6) 可以使函数OutputRoots 执行产生两个实数根的代码，如果输出了2和3，可以有一些信心地认为在本次测试中所执行的代码是正确的。注意，一段错误的代码也可能给出正确的结果。例如，如果在关于 d的表达式中忽略a，将其错误地写成：

T d = b * b - 4 * c;

d的值与所测试的结果相同，因为 a = 1。由于使用测试数据（ 1，-5，6）未能执行完代码中的所有语句，故我们对尚未执行的语句还没有多大的信心。

测试集{(1, -5, 6), (1, 3, 2), (2, 5, 2)} 仅可用来暴露OutputRoots 前7行语句中存在的错误，因为这个测试集中的每个三元组仅需要执行代码的前 7行语句。然而，测试集{(1, -5, 6), (1, -8 ,

16), (1, 2, 5)} 可使OutputRoots 中的每行语句都得到执行，所以该测试集将可以暴露较多的错误。

1.5.2 设计测试数据

在设计测试数据的时候，应当牢记：测试的目标是去披露错误。如果用来寻找错误的测试数据找不到错误，我们就可以有信心相信程序的正确性。为了弄清楚对于一个给定的测试数据，程序是否存在错误，首先必须知道对于该测试数据，程序的正确结果应是什么。

例1-6 对于二次方程求解的例子，可以用如下两种方法之一来给定任意测试数据时程序的正确输出。第一种方法是，计算出所测试二次方程的根。例如，系数（ a, b, c）=(1, -5, 6)的二次方程的根为2和3。对于测试数据（1, -5, 6），可以把程序所输出的根与2和3进行比较，以验证程序1 - 3 0的正确性。第二种可行的方法是把程序所产生的根代入二次函数以验证函数的值是否真为0。所以，如果程序输出的是2和3，可以计算出f (2) = 22-5*2 + 6=0, f ( 3) = 3 2-5 * 3 + 6 = 0。可以把这种验证方法用计算机程序来实现。对于第一种方法，测试程序输入三元组（ a, b, c）和期望的根，然后把程序计算出的根与期望的根进行比较。对于第二种方法，可以编写代码来计算对于程序输出的根，二次函数的相应函数值，然后验证这个值是否为 0。

可以采用下面的条件来计算任何候选的测试数据：

• 这个数据能够发现错误的潜力如何？
• 能否验证采用这个数据时程序的正确性？

设计测试数据的技术分为两类：黑盒法（black box method）和白盒法（white box method）。在黑盒法中，考虑的是程序的功能，而不是实际的代码。在白盒法中，通过检查程序代码来设计测试数据，以便使测试数据的执行结果能很好地覆盖程序的语句以及执行路径。

1. 黑盒法

最流行的黑盒法是I/O 分类及因果图，本节仅探讨I / O分类。在这种方法中，输入数据和 / 或输出数据空间被分成若干类，不同类中的数据会使程序所表现出的行为有质的不同，而相同类中的数据则使程序表现出本质上类似的行为。二次方程求解的例子中有三种本质上不同的行为：产生复数根，产生实数根且不同，产生实数根且相同。可以根据这三种行为把输入空间分为三类。第一类中的数据将产生第一种行为；第二类中的数据将产生第二种行为；而第三类中的数据将产生第三种行为。一个测试集应至少从每一类中抽取一个输入数据。

1. 白盒法

白盒法基于对代码的考察来设计测试数据。对一个测试集最起码的要求就是使程序中的每一条语句都至少执行一次。这种要求被称为语句覆盖（ statement coverage）。对于二次方程求解的例子，测试集{（1, -5, 6），（1，-8，1 6），（1，2，5）} 将使程序中的每一条语句都得以执行，而测试集 {（1，-5，6），（1，3，2），（2，5，2）} 则不能提供语句覆盖。

在分支覆盖（decision coverage）中要求测试集要能够使程序中的每一个条件都分别能出现t r u e和f a l s e两种情况。程序1 - 3 0中的代码有两个条件：d > 0和d = = 0。在进行分支覆盖测试时，要求测试集至少能使条件d > 0和d = = 0分别出现一次为t r u e、一次为f a l s e的情况。

例1-7 [求最大元素] 程序1 - 3 1用于返回数组a [ 0 : n-1 ]中最大元素所在的位置。它依次扫描a [ 0 ]到 a [ n-1 ]，并用变量p o s来保存到目前为止所能找到的最大元素的位置。数据集 a [ 0 : 4 ] = [ 2 , 4 , 6 , 8 , 9 ] 能够提供语句覆盖，但不能提供分支覆盖，因为条件a [ p o s ] < a [ i ]不会变成f a l s e。数据集[ 4，2，6，

8，9 ]既能提供语句覆盖也能提供分支覆盖。

程序1-31 寻找最大元素

template<class T> int Max(T a[], int n)

{// 寻找 a [ 0 : n - 1 ]中的最大元素 int pos = 0;

for (int i = 1; i < n; i++) if (a[pos] < a[i]) pos = i;

return pos;

}

可以进一步加强分支覆盖的条件，要求每个条件中的每个从句（ c l a u s e）既能出现t r u e也能出现f a l s e的情况，这种加强的条件被称之为从句覆盖（clause coverage）。一个从句在形式上被定义成一个不包含布尔操作符（如 & & , | | , !）的布尔表达式。表达式 x > y，x + y < y * z以及c ( c是一个布尔类型)都是从句的例子。考察如下语句：

if((C1 && C2) || (C3 && C4)) S1; else S2;

其中C 1，C 2，C 3和C 4是从句，S 1和S 2是语句。在分支覆盖方式下，需要使用一个能使 ( ( C 1 && C2) || (C3 && C4))为t r u e的测试数据以及一个能使该条件为 f a l s e的测试数据。而从句覆盖则要求测试数据能使四个从句 C 1 , C 2 , C 3和C 4都分别至少取一次t r u e值和至少取一次f a l s e值。还可以继续加强从句覆盖的条件，要求测试各从句值的所有可能组合。对于上面的条件

((C1 && C2) || (C3 && C4))，加强后的从句覆盖要求使用1 6个测试数据集：每个测试集对应于四个从句值组合后的情形。不过，其中有些组合是不可能的。

如果按照某个测试数据集来排列程序语句的执行次序，可以得到一条执行路径（ e x e c u t i o n p a t h）。不同的测试数据可能会得到不同的执行路径。程序 1 - 3 0仅存在三条执行路径——第1行至第7行，第1、2、8～1 2行，第1、2、8、1 3～1 9行。而程序1 - 3 1中的执行路径则随着n的增加而增加。当n= 1时，仅有一条执行路径——1、2、5行；当n= 2时，有两条路径——1、2、3、2、

5和1、2、3、4、2、5行；当n = 3时，有四条路径——1、2、3、2、3、2、5行， 1、2、3、4、

2、3、2、5行，1、2、3、2、3、4、2、5行，1、2、3、4、2、3、4、5行。执行路径覆盖要求测试数据集能使每条执行路径都得以执行。对于二次方程求解程序，语句覆盖、分支覆盖、从句覆盖以及执行路径覆盖都是等价的，但对于程序 1 - 3 1，语句覆盖、分支覆盖、和执行路径覆盖是不同的，而分支覆盖和从句覆盖是等价的。

在这些白盒测试方法中，一般要求实现执行路径覆盖。一个能实现全部执行路径覆盖的测试数据同样能实现语句覆盖和分支覆盖，然而，它可能无法实现从句覆盖。全部执行路径覆盖通常会需要无数的测试数据或至少是非常可观的测试数据，所以在实践中一般不可能进行全部执行路径覆盖。

本书中的许多练习都要求你测试所编代码的正确性。你所使用的测试数据应至少提供语句覆盖。此外，你必须测试那些可能会使你的程序出错的特定情形。例如，对于一个用来对 n≥ 0 个元素进行排序的程序，除了测试n 的正常取值外，还必须测试n= 0 , 1这两种特殊情形。如果该程序使用数组a[0:99], 还需要测试n= 1 0 0的情形。n= 0 , 1和1 0 0分别表示边界条件为空，单值和全数组的情形。

1.5.3 调试

测试能够发现程序中的错误。一旦测试过程中产生的结果与所期望的结果不同，就可以了解到程序中存在错误。确定并纠正程序错误的过程被称为调试（ d e b u g）。尽管透彻地研究程序调试的方法超出了本书的范围，但我们还是提供一些好的建议给大家：

• 可以用逻辑推理的方法来确定错误语句。如果这种方法失败，还可以进行程序跟踪，以确定程序什么时候开始出现错误。如果对于给定的测试数据程序需要运行很多指令，因而需要跟踪太多语句，很难人工确定错误，此时，这种方法就不太可行了，在这种情况下，必须试着把可疑的代码分离出来，专门跟踪这段代码。
• 不要试图通过产生异常来纠正错误。异常的数量可能会迅速增长。必须首先找到需要纠正的错误，然后根据需要重新设计。
• 在纠正一个错误时，必须保证不会产生一个新的、以前没有的错误。用原本能使程序正确运行的测试数据来运行纠正过错误的程序，确信对于该数据，程序仍然正确。
• 在测试和调试一个有错的程序时，从一个与其他函数独立的函数开始。这个函数应该是一个典型的输入或输出函数。然后每次引入一个尚未测试的函数，测试并调试更大一些的程序。

这种策略被称为增量测试与调试（ incremental test and debug）。在使用这种策略时，可以有理由认为产生错误的语句位于刚刚引入的函数之中。练习

1. 证明能够为程序1 - 3 0提供语句覆盖的测试集也能提供分支覆盖和执行路径覆盖。
2. 为程序1 - 3 1设计一个n = 4的测试数据集，要求该测试集能提供执行路径覆盖。
3. 程序1 - 8中有多少条执行路径？ 16. 程序1 - 9中有多少条执行路径？

1.6 参考及推荐读物

1. J.Cohoon, J.Davidson. C++ P rogram Design: An Introduction to Programming and ObjectOriented Design. Richard D.Irwin, 1997。
2. H.Deitel, P.Deitel. C++ How to Pro g r a m. Prentice Hall, 1994。以上两本书是比较好的C + +语言入门教材。
3. G.Myers. The Art of Software Te s t i n g. John Wi l e y, 1979。
4. Boris Beizer. S o f t w a re Testing Techniques 第2版. Van Nostrand Reinhold, 1990。后两本书对于软件测试及调试技术有更透彻的介绍。