ML 02、监督学习
机器学习算法原理、实现与实践——监督学习
机器学习包括监督学习、非监督学习、半监督学习及强化学习,这里先讨论监督学习。
监督学习的任务是学习一个模型,使模型能够对任意给定的输入,对其相应的输出做出一个好的预测。
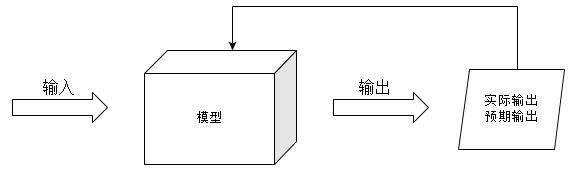
1 基本概念
1.1 输入空间、特征空间与输出空间
输入与输出所有可能取值的集合分别称为输入空间与输出空间。
每个具体的输入是一个实例(instance),通常由特征向量(feature vector)表示,这时,所有特征向量存在的空间称为特征空间。特征空间的每一维对应于一个特征。有时假设输入空间与特征空间为相同的空间。有时假设为不同的空间,这里需要将输入空间映射于特征空间,这一过程称为特征提取。模型实际上都是定义在特征空间上的。在监督学习中,往往把输入空间看为特征空间。通常用$x$表示输入空间的一个实例
$$x = (x^{(1)},x^{(2)},\dots,x^{(i)},x^{(n)})^T$$
其中,$x^{(i)}$表示$x$的第$i$个特征。注意区分$x^{(i)}$与$x_i$,前者是一个实例中的第$i$维特征的值,而后者表示一个训练集中的第$i$个实例,它是一个向量。
监督学习从训练数据集合中学习模型,对测试数据进行预测。训练数据由输入(或特征向量)与输出对组成,训练集通常表示为:
$$T={(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)}$$
测试数据也是由相应的输入与输出对组成。
输入与输出变量均为连续变量的预测问题称为回归问题。输出变量为有限个离散变量的预测称为分类问题;输入变量与输出变量均为变量序列的预测问题称为标注问题。
1.2 联合概率分布
监督学习假设输入与输出的随机变量$X$和$Y$遵循联合概率分布$P(X,Y)$。训练数据与测试数据被看作是依联合概率分布$P(X,Y)$独立同分布产生的。
对于要统计分析的数据,存在这样的联合概率分布$P(X,Y)$,这是监督学习对数据的基本假设。
1.3 假设空间
监督学习的目的在于学习一个输入到输出的映射,这一映射由模型来表示。但这样的映射往往不止一个,学习的目标在于找到最好的这样的模型。由这样的模型构成的集合就是假设空间。
监督学习的模型可以是概率模型或非概率模型。由条件概率分布$P(Y|X)$或决策函数$Y=f(X)$表示。
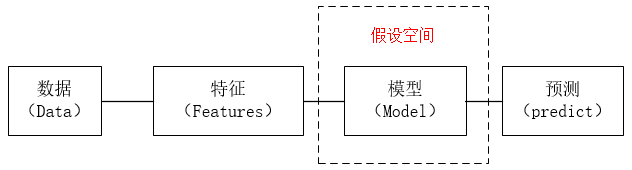
2 监督问题的形式化表示
监督学习利用训练数据集学习一个模型,再用模型对测试样本集进行预测。由于在这个过程中需要训练数据集,而训练数据集往往是人工给出的,所以称为监督学习。
监督学习分为学习和预测两个过程,由学习系统与预测系统完成,可以描述为下图。
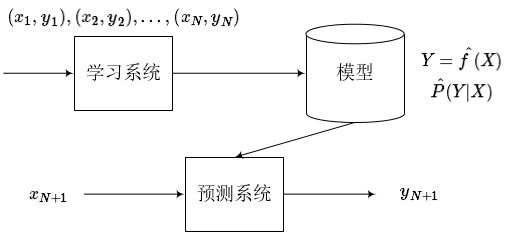
首先给定一个训练数据集:
$$T={(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)}$$
其中$(x_i,y_i),i=1,2,\dots,N$,称为样本或样本点。$x_i$为一个输入的观测值,$y_i$为输出的观测值。
监督学习中,假设训练数据与测试数据是依联合概率分布$P(X,Y)$独立同分布产生的。
在学习的过程中,学习系统利用给定的训练数据集,通过学习得到一个模型,表示为条件概率分布$\hat{P}(Y|X)$或决策函数$Y=\hat{f}(X)$。
在预测过程中,预测系统对给定的测试样本集中的输入$x_{N+1}$,由模型$Y_{N+1} = arg \max_{y_{N+1}}\hat{P}(y_{N+1}|x_{N+1})$或$y_{N+1} = \hat{f}(x_{N+1})$给出相应的输出$y_n+1$
在学习的过程中,每一个$(x_i,y_i)$都会给模型带来一些信息,具体地说就是,对于输入$x_i$,一个具体的模型$y=f(x)$会产生一个输出$f(x_i)$,然后用$f(x_i)$与训练样本的输出$y_i$对比,然后学习模型会根据这个差距适当的自我调整,以保证下次再遇到$x_i$这个输入时,预测的比现在好。