3-1 无向图的连通分量的个数
联通图和非联通图:
在无向图中,若从顶点 u 到 v 有路径,则称顶点 u 和 v是连通的(connected)。
如果无向图中任意一对顶点都是连通的,则称此图是连通图(connected graph);
相反,如果一个无向图不是连通图,则称为非连通图(disconnected graph)。
如果一个无向图不是连通的,则其极大连通子图称为连通分量(connected component)
图使用邻接表 表示,文件内容为:
7 6
0 1
0 2
1 3
1 4
2 3
2 61. 类 Graph,实现邻接表生成图
package graphDFS;
import java.io.File;
import java.io.IOException;
import java.util.TreeSet;
import java.util.Scanner;
//只是处理简单的图,使用红黑树
public class Graph {
private int V; // 图的顶点的数量
private int E; // 图的边的数量
private TreeSet[] adj; // 将每个点保存在一个链表当中
public Graph(String filename) {
File file = new File(filename);
try {
// 读取文件
Scanner scanner = new Scanner(file);
V = scanner.nextInt();
// 判断顶点数量是否有误
if (V < 0) throw new IllegalArgumentException("V 必须是个不为负数的数值");
adj = new TreeSet[V]; // 创建链表
for (int i = 0; i < V; i++) {
adj[i] = new TreeSet<>(); // 对于每个顶点创建一个链表
}
E = scanner.nextInt();
if (E < 0) throw new IllegalArgumentException("E 必须是个不为负数的数值");
for (int i = 0; i < E; i++) { // 遍历边的数量就可以了
int a = scanner.nextInt();
validateVertex(a);
int b = scanner.nextInt();
validateVertex(b);
// 判断是否是自环边
if (a == b) throw new IllegalArgumentException("不允许存在自环边");
// 此时红黑树的遍历复杂度为 O(logN)
if (adj[a].contains(b)) throw new IllegalArgumentException("不允许存在平行边");
adj[a].add(b); // 复杂度为 O(N)
adj[b].add(a); // 将数据保存在链表中
}
} catch (IOException e) {
e.printStackTrace();
}
}
private void validateVertex(int v) {
if (v < 0 || v > V) {
throw new IllegalArgumentException("输入的数值" + v +"不合法");
}
}
// 获取指定结点相邻的结点
public Iterable adj(int v){
validateVertex(v);
return adj[v];
}
// 获取指定结点的度,即相邻的结点的数量
public int degree(int v) {
validateVertex(v);
return adj[v].size();
}
public int V() {
return V;
}
public int E() {
return E;
}
public boolean hasEdge(int x, int y) { // 依据两个顶点判断边是否存在
validateVertex(x);
validateVertex(y);
return adj[x].contains(y);
}
public String toString() {
StringBuilder stringBuilder = new StringBuilder();
stringBuilder.append(String.format("V = %d, E = %d \n", V, E));
// 打印出矩阵
for (int v =0; v< V; v++) {
stringBuilder.append(String.format("%d : ", v));
for (int w: adj[v]) { // 遍历链表
stringBuilder.append(String.format(" %d ", w));
}
stringBuilder.append("\n");
}
return stringBuilder.toString();
}
// public static void main(String[] args) {
// Graph adjMatrix = new Graph("g3.txt");
// System.out.println(adjMatrix);
// System.out.println(adjMatrix.adj(2).toString());
// System.out.println(adjMatrix.degree(2));
//
// }
}
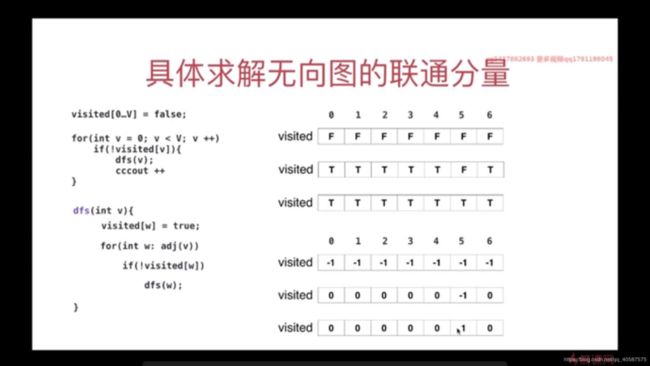
2. java实现求解无向图的连通分量的个数。
package graphDFS;
import java.util.ArrayList;
// 实现无向图的联通分量的个数
public class CC {
// 创建一个数组,
private int ccCount = 0; // 联通分量的个数
private boolean[] visited;
private Graph graph;
public CC(Graph graph) {
this.graph = graph;
visited = new boolean[graph.V()]; // 结点的数量
//dfs(0);
// 改进的地方:对每一个结点进行遍历
for (int v = 0; v < graph.V(); v++) {
if (!visited[v]) {
dfs(v);
ccCount ++; // 对联通分量分数累加
}
}
}
private void dfs(int v) {
visited[v] = true;
for (int w: graph.adj(v)) { // 遍历该节点的相邻结点
if (! visited[w])
dfs(w);
}
}
public int count(){
return ccCount;
}
public static void main(String[] args) {
Graph graph = new Graph("g3.txt");
CC graphDFS = new CC(graph);
System.out.println(graphDFS.count()); //计算得到 2 个联通分量
}
}
3-2 求解一个联通分量的所有顶点
设置一个顶点数量大小的数组,数组中相同的数字来自于同一个联通分量。
package graphDFS;
import java.util.ArrayList;
import com.sun.org.apache.bcel.internal.generic.IRETURN;
// 实现无向图的联通分量的个数
public class CCTwo {
// 创建一个数组,
private int ccCount = 0; // 联通分量的个数
private int[] visited; // 将其存为数组型,保存更多信息
private Graph graph;
public CCTwo(Graph graph) {
this.graph = graph;
visited = new int[graph.V()];
for (int i = 0; i < graph.V(); i++) { // 对数值初始化,-1 表示没有遍历
visited[i] = -1;
}
//dfs(0);
// 改进的地方:对每一个结点进行遍历
for (int v = 0; v < graph.V(); v++) {
if (visited[v] == -1) {
dfs(v, ccCount);
ccCount ++; // 对联通分量分数累加
}
}
}
private void dfs(int v, int ccid) {
visited[v] = ccid;
for (int w: graph.adj(v)) { // 遍历该节点的相邻结点
if (visited[w] == -1)
dfs(w, ccid);
}
}
public int count(){
for (int e:visited) {
System.out.print(e + " ");
}
System.out.println();
return ccCount;
}
public boolean isConnected(int v, int w) { // 判断两点是否是在同一个联通分量
graph.validateVertex(v);
graph.validateVertex(w);
return visited[v] == visited[w];
}
// 获取联通分量的元素
public ArrayList[] components() {
ArrayList[] res = new ArrayList[ccCount];
for (int i = 0; i< ccCount; i++) {
res[i] = new ArrayList<>();
}
for (int i = 0; i < graph.V(); i++) {
res[visited[i]].add(i);
}
return res;
}
public static void main(String[] args) {
Graph graph = new Graph("g3.txt");
CCTwo graphDFS = new CCTwo(graph);
System.out.println(graphDFS.count()); //计算得到 2 个联通分量
for (int i =0 ; i < graphDFS.components().length; i++) {
System.out.print(i + " : ");
for(int e: graphDFS.components()[i]) {
System.out.print(e + " ");
}
System.out.println();
}
// 0 0 0 0 0 1 0 // 0 和 1 表示不同的分量
// 2
}
}
3-3 单源路径问题的编程实现
两点在同一个联通分量,则意味着两点之间有路径。
package graphDFS;
import java.util.ArrayList;
import java.util.Collections;
public class SingleSourthPath {
private int s; // 传入的顶点
private boolean[] visited;
private int[] pre; // 对连接的前一个结点进行记录
private Graph graph;
public SingleSourthPath(Graph graph,int s) {
this.graph = graph;
this.s = s;
graph.validateVertex(s);
visited = new boolean[graph.V()];
pre = new int[graph.V()];
for (int i = 0; i < pre.length; i++) {
pre[i] = -1;
}
dfs(s, s);
}
private void dfs(int v, int parent) { // 需要知道前一个相连接的结点parent
visited[v] = true;
pre[v] = parent;
for (int w: graph.adj(v)) { // 遍历该节点的相邻结点
if (! visited[w])
dfs(w, v);
}
}
public void showPre(){
System.out.print("pre : ");
for (int e: pre) {
System.out.print( e + " ");
}
System.out.println();
}
public boolean isConnected(int t) { // 查看顶点是否在联通分量上
graph.validateVertex(t);
return visited[t];
}
public Iterable path(int t){ // 到 t 点的路径
ArrayList res = new ArrayList<>();
if (! isConnected(t)) return res;
int cur = t;
while (cur != s) {
res.add(cur);
cur = pre[cur];
}
res.add(s);
Collections.reverse(res);
return res;
}
public static void main(String[] args) {
Graph graph = new Graph("g3.txt");
SingleSourthPath graphDFS = new SingleSourthPath(graph,0);
graphDFS.showPre();
System.out.println("0 -> 6: " + graphDFS.path(6)); // 0 到 6 的路径
// 0 -> 6: [0, 1, 3, 2, 6]
}
}
。。。。。。。。。。。。。end。。。。。。。。。。。。。