齐姐漫画：排序算法（二）之「归并排序」和「外排序」

那我们借用 cs50 里的例子，比如要把一摞卷子排好序，那用并归排序的思想是怎么做的呢？

首先把一摞卷子分成两摞；
把每一摞排好序；
把排好序的两摞再合并起来。

感觉啥都没说？
那是因为上面的过程里省略了很多细节，我们一个个来看。

首先分成两摞的过程，均分，奇偶数无所谓，也就是多一个少一个的问题；
那每一摞是怎么排好序的？

答案是用同样的方法排好序。

排好序的两摞是怎么合并起来的？

这里需要借助两个指针和额外的空间，然后左边画一个彩虹右边画个龙，不是，是左边拿一个数，右边拿一个数，两个比较大小之后排好序放回到数组里（至于放回原数组还是新数组稍后再说）。

这其实就是分治法 divide-and-conquer 的思想。
归并排序是一个非常典型的例子。

分治法

顾名思义：分而治之。

就是把一个大问题分解成相似的小问题，通过解决这些小问题，再用小问题的解构造大问题的解。

听起来是不是和之前讲递归的时候很像？

没错，分治法基本都是可以用递归来实现的。

在之前，我们没有加以区分，当然现在我也认为不需要加以区分，但你如果非要问它们之间是什么区别，我的理解是：

递归是一种编程技巧，一个函数自己调用自己就是递归；
分治法是一种解决问题的思想：
- 把大的问题分解成小问题的这个过程就叫“分”，
- 解决小问题的过程就叫“治”，
- 解决小问题的方法往往是递归。

所以分治法的三大步骤是：

「分」：大问题分解成小问题；

「治」：用同样的方法解决小问题；

「合」：用小问题的解构造大问题的解。

那回到我们的归并排序上来：

「分」：把一个数组拆成两个；

「治」：用归并排序去排这两个小数组；

「合」：把两个排好序的小数组合并成大数组。

这里还有个问题，就是什么时候能够解决小问题了？

答：当只剩一个元素的时候，直接返回就好了，分解不了了。
这就是递归的 base case，是要直接给出答案的。

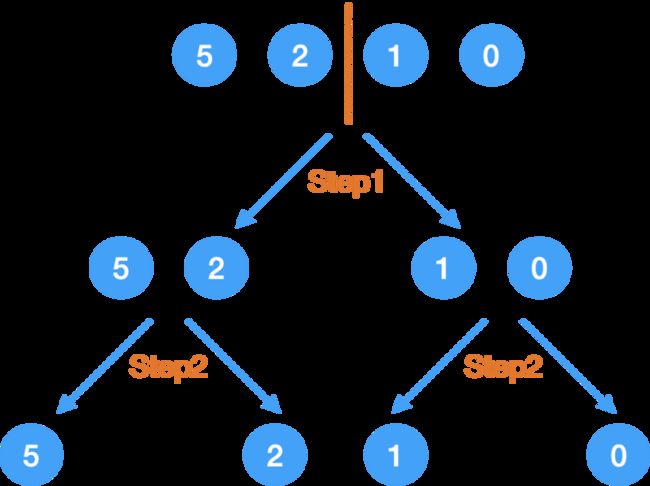
老例子：{5, 2, 1, 0}

暗示着齐姐对你们的爱啊～❤️

Step1.

先拆成两半，
分成两个数组：{5, 2} 和 {1, 0}

Step2.

没到 base case，所以继续把大问题分解成小问题：

当然了，虽然左右两边的拆分我都叫它 Step2，但是它们并不是同时发生的，我在递归那篇文章里有说原因，本质上是由冯诺伊曼体系造成的，一个 CPU 在某一时间只能处理一件事，但我之所以都写成 Step2，是因为它们发生在同一层 call stack，这里就不在 IDE 里演示了，不明白的同学还是去看递归那篇文章里的演示吧。

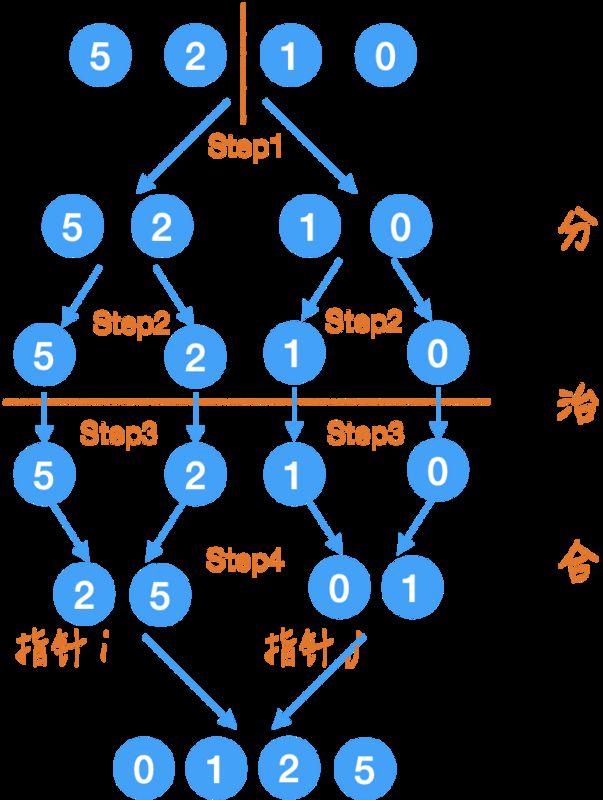
Step3.

这一层都是一个元素了，是 base case，可以返回并合并了。

Step4.

合并的过程就是按大小顺序来排好，这里借助两个指针来比较，以及一个额外的数组来辅助完成。

比如在最后一步时，数组已经变成了：
{2, 5, 0, 1}，
那么通过两个指针 i 和 j，比较指针所指向元素的大小，把小的那个放到一个新的数组？里，然后指针相应的向右移动。

其实这里我们有两个选择：

一种是从新数组往原数组合并，
另一种就是从原数组往新数组里合并。

这个取决于题目要求的返回值类型是什么；以及在实际工作中，我们往往是希望改变当前的这个数组，把当前的这个数组排好序，而不是返回一个新的数组，所以我们采取从新数组往原数组合并的方式，而不是把结果存在一个新的数组里。

那具体怎么合并的，大家可以看下15秒的小动画：

挡板左右两边是分别排好序的，那么合并的过程就是利用两个指针，谁指的数字小，就把这个数放到结果里，然后移动指针，直到一方到头（出界）。

public class MergeSort {
public void mergeSort(int[] array) {
    if(array == null || array.length <= 1) {
        return;
    }
    int[] newArray = new int[array.length];
    mergeSort(array, 0, array.length-1, newArray);
}
private void mergeSort(int[] array, int left, int right, int[] newArray) {
  // base case
    if(left >= right) {
        return;
    }

  // 「分」
    int mid = left + (right - left)/2;
    
  // 「治」
  mergeSort(array, left, mid, newArray);
    mergeSort(array, mid + 1, right, newArray);
    
  // 辅助的 array
    for(int i = left; i <= right; i++) {
        newArray[i] = array[i];
    }
    
  // 「合」
    int i = left;
    int j = mid + 1;
    int k = left;
    while(i <= mid && j <= right) {
        if(newArray[i] <= newArray[j]) { // 等号会影响算法的稳定性
            array[k++] = newArray[i++];
        } else {
            array[k++] = newArray[j++];
        }
    }
    if(i <= mid) {
        array[k++] = newArray[i++];
    }
}
}

写的不错，我再来讲一下：

首先定义 base case，否则就会成无限递归死循环，那么这里是当未排序区间里只剩一个元素的时候返回，即左右挡板重合的时候，或者没有元素的时候返回。

「分」

然后定义小问题，先找到中点，

那这里能不能写成 (left+right)/2 呢？
注意⚠️，是不可以的哦。

虽然数学上是一样的，
但是这样写，
有可能出现 integer overflow.

「治」

这样我们拆好了左右两个小问题，然后用“同样的方法”解决这两个自问题，这样左右两边就都排好序了～

为什么敢说这两边都排好序了呢？
因为有数学归纳法在后面撑着～

那在这里，能不能把它写成：

mergeSort(array, left, mid-1, newArray);
mergeSort(array, mid, right, newArray);

也就是说，

左边是 [left, mid-1]，
右边是 [mid, right]，

这样对不对呢？

答案是否定的。

因为会造成无限递归。

最简单的，举个两个数的例子，比如数组为{1, 2}.

那么 left = 0, right = 1, mid = 0.

用这个方法拆分的数组就是：

[0, -1], [0, 1] 即：
空集，{1, 2}

所以这样来分并没有缩小问题，没有把大问题拆解成小问题，这样的“分”是错误的，会出现 stack overflow.

再深一层，究其根本原因，是因为 Java 中的小数是「向零取整」。

所以这里必须要写成：

左边是 [left, mid]，
右边是 [mid + 1, right]。

「合」

接下来就是合并的过程了。

在这里我们刚才说过了，要新开一个数组用来帮助合并，那么最好是在上面的函数里开，然后把引用往下传。开一个，反复用，这样节省空间。

我们用两个指针：i 和 j 指向新数组，指针 k 指向原数组，开始刚才动画里的移动过程。

要注意，这里的等于号跟哪边，会影响这个排序算法的稳定性。不清楚稳定性的同学快去翻一下上一篇文章啦～

那像我代码中这种写法，指针 i 指的是左边的元素，遇到相等的元素也会先拷贝下来，所以左边的元素一直在左边，维持了相对顺序，所以就是稳定的。

最后我们来分析下时空复杂度：

时间复杂度

归并排序的过程涉及到递归，所以时空复杂度的分析稍微有点复杂，在之前「递归」的那篇文章里我有提到，求解大问题的时间就是把所有求解子问题的时间加起来，再加上合并的时间。

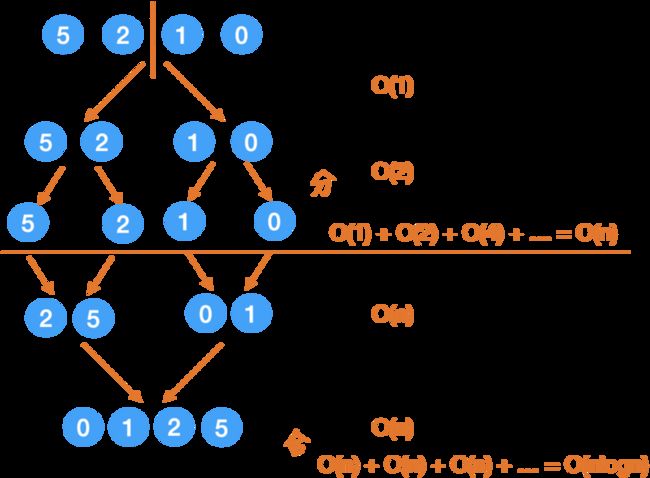
我们在递归树中具体来看：

这里我右边已经写出来了：

「分」的过程，每次的时间取决于有多少个小问题，可以看出来是
1，2，4，8...这样递增的，
那么加起来就是O(n).

「合」的过程，每次都要用两个指针走完全程，每一层的 call stack 加起来用时是 O(n)，总共有 logn 层，所以是 O(nlogn).

那么总的时间，就是 O(nlogn).

空间复杂度

其实归并排序的空间复杂度和代码怎么写的有很大的关系，所以我这里分析的空间复杂度是针对我上面这种写法的。

要注意的是，递归的空间复杂度的分析并不能像时间复杂度那样直接累加，因为空间复杂度的定义是在程序运行过程中的使用空间的峰值，本身就是一个峰值而非累加值的概念。

那也就是 call stack 中，所使用空间最高的时刻，其实就是递归树中最右边的这条路线：它既要存着左边排好序的那半边结果，还要把右边这半边继续排，总共是 O(n).

那有同学说 call stack 有 logn 层，为什么不是 O(logn)，因为每层的使用的空间不是 O(1) 呀。

扩展：外排序

这两节介绍的排序算法都属于内部排序算法，也就是排序的过程都是在内存中完成。

但在实际工作中，当数据量特别大时，或者说比内存容量还要大时，数据就无法一次性放入内存中，只能放在硬盘等外存储器上，这就需要用到外部排序算法算法来完成。一个典型的外排序算法就是外归并排序（External Merge Sort）。

这才是一道有意思的面试题，在经典算法的基础上，加上实际工作中的限制条件，和面试官探讨的过程中，就能看出 candidate 的功力。

要解决这个问题，其实是要明确这里的限制条件是什么：

首先是内存不够。那除此之外，我们还想尽量少的进行硬盘的读写，因为很慢啊。

比如就拿wiki上的例子，要对 900MB 的数据进行排序，但是内存只有 100MB，那么怎么排呢？

wiki 中给出的是读 100MB 数据至内存中，我并不赞同，因为无论是归并排序还是快排都是要费空间的，刚说的空间复杂度 O(n) 不是，那数据把内存都占满了，还怎么运行程序？那我建议比如就读取 10MB 的数据，那就相当于把 900MB 的数据分成了 90 份；
在内存中排序完成后写入磁盘；
把这 90 份数据都排好序，那就会产生 90 个临时文件；
用 k-way merge 对着 90 个文件进行合并，比如每次读取每个文件中的 1MB 拿到内存里来 merge，保证加起来是小于内存容量且能保证程序能够运行的。

那这是在一台机器上的，如果数据量再大，比如在一个分布式系统，那就需要用到 Map-Reduced 去做归并排序，感兴趣的同学就继续关注我吧～

齐姐漫画：排序算法（二）之「 归并排序」和「外排序」

分治法