Study on Algorithm of Selecting Safe Landing Area on Ground During Asteroid Soft Landing (EEIC2013 +161)

OUATTARA Sie, RUAN Xiaogang, Yan yan

Institute of Artificial Intelligence and Robots, School of Electronic Information and Control Engineering

Beijing University of Technology Beijing, China  

[email protected] ; [email protected] ; [email protected]

 

Abstract—For the selection a safe area during landing on asteroid, this article proposes an algorithm of selecting safe landing area based on binaryzation combined with morphology. First, it provides a new binary algorithm for highlighting the shadow area and the lighting area. Second, in order to dilate the shadow area and the lighting area by Using of algorithm of dilatation of morphology. Last, choosing the bigger area which is not dilated as the final safe landing area. The algorithm raised in the article is tested and proved by a group images of asteroid topography.

Introduction 

Obstacles, including rocks, slopes, meteorite crater and cliff, will be the great potential dangers when astrovehicle is landing [1, 2]. It is difficult to control the astrovehicle simultaneously because of the great distance between the probing planet and the earth. Therefore it is especially important to detect the obstacles and select the safe landing area [1, 2]. At present, there are two ways of obstacles’ detection as follows: one is obstacle detection algorithm based on laser radar or wireless radar [3]. The author of the reference [4, 5] provides obstacle detection algorithm based on laser radar; And in [6], the author raises obstacle detection algorithm based on DEM radar. The other is the obstacle detection algorithm based on the photos taken when asteroid is landing. In reference [7], the author brings forward the detection algorithm of rock and meteorite crater based on the image. The reference [3] proposes the shadow area projecting algorithm of Gaussian pyramid and Multiple Sequential Gray Thresholds for detecting the obstacles.

Because the shadow area and lighting area can reflect the position, size and shape of the Rocks, meteorite crater, topography and others of the image, this article proposes an obstacle detection algorithm based on the binaryzation. First, it provides a new binary algorithm, which may detect the shadow area and the lighting area. Then the detected shadow area and lighting area will be dilated in the binary image. Finally, the big-sized undilated area will be the safe landing area. The algorithm diagram in Fig. 1:

                                

Figure 1.  Algorithm Diagram

 

This template provides authors with most of the formatting specifications needed for preparing electronic versions of their papers. All standard paper components have been specified for three reasons: (1) ease of use when formatting individual papers, (2) automatic compliance to electronic requirements that facilitate the concurrent or later production of electronic products, and (3) conformity of style throughout a conference proceeding. Margins, column widths, line spacing, and type styles are built-in; examples of the type styles are provided throughout this document and are identified in italic type, within parentheses, following the example. PLEASE DO NOT RE-ADJUST THESE MARGINS. Some components, such as multi-leveled equations, graphics, and tables are not prescribed, although the various table text styles are provided. The formatter will need to create these components, incorporating the applicable criteria that follow.

                               I.    IMAGE BINARYZATION

The most popular binaryzation algorithm is Otsu [8], which is a global threshold algorithm that was proposed in 1979. But when the image has uneven brightness, it cannot get the ideal result. LIANG Huawei proposed an algorithm determined by binary threshold for double peak histogram, which has a limitation that cannot be used in Multi-Peak Value situation. This article introduces a self-adaptive determined algorithm of Binary threshold of shadow and Bright Areas. It can extract the shadow part and the lighting part from the stars’ surface image of the photo. In order to determine the safe landing area, it extracts the strong lighting area. The following is the details about the algorithm.

 

A. Search for Pixel Value of Acnode of the Image Based on Least Square Method 

Acnode [10] usually is defined as the more special data in a data set. Let data set S be the statistical quantity of every pixel value of an image. That is ： s(i)∈S ， i = 0,1L255，and i +1> i , this article gets the curve l using the least-square method, in which i is the abscissa and l(i) is the ordinate. This curve is used to fit the curve s . 

Lemma 1:  Let d(i) = s(i) - l(i),i = 0L255， when act j as the acnode of S ：

               d( j) > 0 and        1     e -(d (^2σj)-²µ)² _<< p                 (1)

2πσ

Among themµ ;

 

Proof: Curve l is the fitting curve of S . d(i) is the

Euclidean distance between s(i) and l(i) .When it is d( j) < 0 , and s( j) <l( j) , the image will not be influenced by pixel value of j . But when it is d( j) > 0 , the pixel value of j is bigger than the corresponding values of fitting curve，it will be much more possible to have the acnode. Because d approximately obey normal distribution

of N(_µ,_σ) and d ’s average probability is p , when j is the acnode  of S , which shows j is the minimal probability value of d . So the probability of d( j) should be much smaller than the average probability value of d . In this -(d ( j)- )²

article ： when ^， j is the acnode pixel value of S .

The pixel value of acnode in the image is the number of pixel value account for maximum proportion of the image. It may influence the brightness spreading of the image, which effact the get the average pixel value about the whole image. When there exists the acnode pixel, it should be endowed with the average value of the un-acnode pixel. Thus it may reduce the overall influence of acnode for the average pixel value.

First, confirm that you have the correct template for your paper size. This template has been tailored for output on the US-letter paper size. If you are using A4-sized paper, please close this template and download the file for A4 paper format called “CPS_A4_format”.

B. A Self-adaptive Determined algorithm of Binary threshold of shadow and Bright Areas (DBT)

 

This algorithm studies the High value (which is bigger than the average grey) and the Low value (which is lower than the average grey) separately. During the process, arrange the difference value between High value and average value in order of size from big to small. While arrange the difference value between Low value and average value in order of size from small to big. Then through analysis of the changing rate of this two group values to find the high change rate section. The pixel value corresponding those in the high change rate section are more obvious than other pixels among the High value and the Low value. Finally, calculate the standard difference between the corresponding value and the average value. The relationship of standard difference and the average value can determine that two binary thresholds (in shadow area and lighting area).See the following details:

Step1: calculate the average value of grey of the image： f = M 1 N ∑M= ∑N= f (x, y)  (2)

× x 1 y 1

 

Among them：M  is the row number of the image and

N is the column number. f (x, y) is the pixel value in the position of(x, y).

Step2: b₁ is the set of pixel value less than f ；b₂  is

the set of pixel value more than f . And arrange b₁ in ascending order and b₂ in descending order.

b₁ :b₁ (i) _≤ f (i =1Ln₁) ^and b₁(i +1) ≥ b₁(i) (3)

b₂ :b₂ ( j) _> f ( j =1Ln₂) and b₂( j +1) ≤b₂( j)(4)

Among them, n₁and n₂ are the number of low value and high value. 

Step3: Calculate the difference value b₁ and b₂ set

between b₁ and f &b₂ and f separately: 

b₁^' (i) ₌b₁ (i) - f , (i =1Ln₁ )           (5) b₂^' (i) ₌b₂ (i) - f , (i =1Ln₂ )                 (6)

Step4: Calculate the change rate of b₁^' and b₂^' to get two

new sets v₁ and v₂ ; and get its average value v₁ andv₂ v          (7)

v1       n₁ -1 _i=₁ 1                                                     (8) v      (9)

                                  v2 = n21-1∑nj2=-11v2 ( j)                    (10)

 

Step5: Calculate Maximum position L₁ which is bigger than v₁ in v₁ ; Calculate Maximum position L₂ which is smaller than v₂ in v₂

L₁ : v₁ (L₁ ) = max(v₁ (i) > v₁ )  (i =1Ln₁ -1) (11)

L₂ : v₂ (L₂ ) = max(v₂ ( j) < v₂ )  ( j =1Ln₂ -1) (12)

Therefore, L₁and L₂ are the high change interval length.

Step6: Calculate length scale p₁ of L₁ in v₁ ; and length scale p₂ of L₂ in v₂：

p₁ = L₁/(n₁ −1)  (13) p₂ = L₂/(n₂ -1)  (14)

Step7: Calculate the standard difference f₁^' and f ₂^' of every high change area in b₁ and b₂：

n1×p1

                             f₁^' = ∑b₁^' (i) ² /(n₁ × p₁ )                      (15)

i=1 n2×p2

                             f ₂^' = ∑b₂^' (i) ² /(n₂ × p₂ )                     (16)

j=1

Step8: get the threshold α₁ of shadow area and α₂ of lighting area：

                               a2                     b2                    c2

Figure 2.  Binary Design sketch

 

Fig. 2 includes the shadow area and the lighting area, which are acquired by binary algorithm under different lighting conditions. b,b1,b2 are the binary result of shadow area; c,c1,c2 are the binary result in lighting area.

 

                       II.   DILATATION OF BINARY IMAGE

This article deal with the binary image by using dilation of morphology for finding the suitable area. Suppose M, N are both sets in R (two-dimensional space). Here N is called as structural element. M is dilated by N and defined as:

∧

                                M⊕N = {a | (N)_a IM ≠Φ}             (19)

Among  {w | w =−n,n∈ N} , shows the reflection for N.

        a,n       , shows translate the

reflection of N to the position of a = (a₁,a₂).

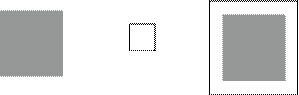
In Fig. 3, if a is the set M, c acts as the structure element N and its mapping. N is equal to its mapping, should be Symmetric about the Origin. C is the result that M is dilated for N. The white area is the dilated area.

        a: M                             b: N                       c:        M_⊕:N               

Figure 3.  Diagram of Dilatation Algorithm

 

Using dilatation theory to look for character of the target has good reason. It chooses the structure with the size of n^×n to dilatate the binary topographic map. All the lighting point is dilated by the structure. Even the smallest size is nearly reached n/2 . After dilatation, the black part in the image is flat and smooth, more far away from the obstacles.

 

            III.   THE CHOSEN OF THE SAFE LANDING AREA  

Choosing the safe landing area in the image which has been dilated binarily should be following the rules as shown in bellow:

（1）   For let the chosen landing area to be near the central part of the image, if M1 × M2 is the original size, n1 ×n2 is the structure size, the original image should delete the n1and n2 of the both ends of length and width and get the result （M1 -2×n1)×(M2 -2×n2) .

（2）   The size of landing area is usually the maximum inscribed rectangular of the undilated area. 

（3）   For convenience to track the chosen landing area, it is better exist some reference feature like rocks and meteor crater around it. Therefore, it may develop the real-time navigation for the space machine

using the center of safe landing area as the target and reference feature as the landmark.

 

 

                       IV.   EXPERIMENTS AND ANALYSIS

 Figure 4.  Image of experiment

 

This article uses the pictures of Small Bodies 433 EROS of NEAR exploration in 2001 to test the performance of the algorithm. As showing in Fig. 4, from picture a to d, the high of shot is from high to low, and there exists the big different lighting condition. In this experiment, it introduces the projecting experiment for shadow area and lighting area of binary algorithm for the four pictures in Fig. 4. As Fig.5 showing:

 Figure 5.  Binary image

 

Seeing from Fig. 5, shadow area and lighting area in Fig. 4 has been shown very well. The following is using dilatation algorithm to dilatate the shadow area and lighting area in Fig. 5. The size of the dilated structure may be adjusted according to the image size. Usually, the side length of structure should be the 1/20 of the minimum side length of the image. The size of the four pictures of this article is 388x496. Therefore, the size of the structure is 20x20.

 

Figure 6.  The effect picture of dilated binary image

 

Fig. 6 is the dilated picture of the binary image in Fig. 5. Seeing from the picture, the shadow area and lighting area are enlarged obviously, the undilated area has not the obstacles, which has a distance from the area with obstacles. This area can be the safe landing area for the space machine. According to the above rules, the red rectangular area can be the best choice for safe landing. While there exists much more noise and more complicated texture, which decrease the size of safe landing area in the dilated image. For this can use the filter to filt the noise and the trivial texture.

The algorithm in this article is real-time effectively, which calculates the four images of Fig. 4 only in 1 second separately.

 

                                       V.    CONCLUSION

This article provides an algorithm for searching safe landing, which focus on dilatation of binary image for shadow area and lighting area. There are several advantages: (1) it is a new binary algorithm for extracting shadow area and lighting area in the image. (2) Using morphologic dilatation to dilatate shadow area and lighting area in the binary image shows the improvement of safe landing for the space machines. (3) This algorithm is real-time and timesaving, which is valid for choosing the safe landing area.

There also has some limitation of this algorithm. One is the threshold in shadow area and lighting area of binary algorithm is the global threshold, which has uncertainty under the circumstance of the more complicated topography and lighting condition. The other is the filter for the noise and complexes texture in the image should be chosen one more suitable to deal with the image. 

 

REFERENCES

 

[1]     M. P. Golombek, et al. "Assessment of Mars Exploration Rover landing site predictions," Nature, London, vol. 436.7047, pp. 44-48, July 2005.

[2]     J. A. Grant, et al. "Selecting landing sites for the 2003 Mars Exploration Rovers," Planet. Space. Sci. England, vol. 52.1, pp. 11-21, January 2004.

[3]     Z. X. Zhang, W. D. Wang, and P. Y. Cui, "A reliable algorithm of rock detection and avoidance for safe spacecraft landing," 2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics (ISSCAA), Harbin, pp. 1009-1013, June 2010.       

[4]     A. E. Johnson, A. R. Klumpp, J. Collier, and A. Wolf, "LIDAR-based hazard avoidance for safe landing on Mars," J. Guid. Control. Dyn. Vol. 25, no. 6, pp. 1091-1099, November 2002.

[5]     A. E. Johnson, E. Skulsky, M. Bajracharya, and E. Wong. "Design of a Hazard Detection and Avoidance System for the Mars Smart Lander (AIAA-2002-4620)," In AIAA Atmospheric Flight Mechanics Conference, Monterey, CA. 2002.

[6]     Andrew E.Johnson,Andres Huertas. “Analysis of on board hazard detection and avoidance for safe lunar landing”. In Aerospace Conference, 2008 IEEE. Big Sky, MT, pp. 1-9, March 2008

[7]     D.E. Bernard, M.P. Golombek, “Crater and rock hazard modeling for Mars landing”, In proceedings of AIAA Space Conference. 2001 

[8]     N. Otsu, "A threshold selection method from gray-level histograms," IEEE Trans. Syst. Man Cybern. vol. New York, SMC-9(1), pp. 62-66, January 1979.

[9]     H. W. Liang, "Direct determination of threshold from bi-modal histogram," Pattern. Recognit. Artif. Intell. Hefei, Vol. 15(2), pp. 253256, June 2002.

[10]  H. Cao, G. Q. Si, and Y. B. Zhang. "A density-neighbors-based incremental outlier detection algorithm." Pattern. Recognit. Artif. Intell. Hefei, Vol. 22(6), pp. 931-935, December 2009

[11]  Rafael C. Gonzalez, Richard E. “Digital Image Processing. Pearson

Education“. Gatesmark Publishing, 2009, pp. 15-267