对于fmri的设计矩阵构造的一个很直观的解释-by 西南大学xulei教授
本程序意在解释这样几个问题:完整版代码在本文的最后。
1.实验的设计如何转换成设计矩阵? 2.设计矩阵的每列表示一个刺激条件,如何确定它们? 3.如何根据设计矩阵和每个体素的信号求得该体素对刺激的敏感性?
程序详解:
1.构造hrf
hrf_small = [ 0 4 2 -1 0 ];
figure(1);
clf;
plot(0:4,hrf_small,'o-');
grid on;
xlabel('Time (in units of TRs, 4s long each)');
ylabel('fMRI signal');
title('This is what an HRF would look like if you measure once every 4s')

2.构造刺激序列,并与hrf做卷积:
word_stim_time_series = [ 0 1 0 0 0 0 ];
object_stim_time_series= [ 0 0 0 1 0 0 ];
predicted_signal_that_word_would_evoke = conv(word_stim_time_series,hrf_small);
predicted_signal_that_object_would_evoke = conv(object_stim_time_series,hrf_small);
figure(2);
clf;
subplot(3,1,1);
hold on;
h1=stem(word_stim_time_series,'b');
h2=stem(object_stim_time_series,'r');
hold off;
grid on;
legend([h1(1) h2(1)],'Word stim onset time','Object stim onset time');
axis([1 9 0 1.2]);
ylabel('Stimulus present / absent');
subplot(3,1,2);
plot(predicted_signal_that_word_would_evoke,'b*-');
grid on;
legend('Word-sensitive voxel would give this fMRI signal');
axis([1 10 -1.5 7]);
ylabel('fMRI signal');
subplot(3,1,3);
plot(predicted_signal_that_object_would_evoke,'r^-');
grid on;
legend('Object-sensitive voxel would give this fMRI signal');
axis([1 10 -1.5 7]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
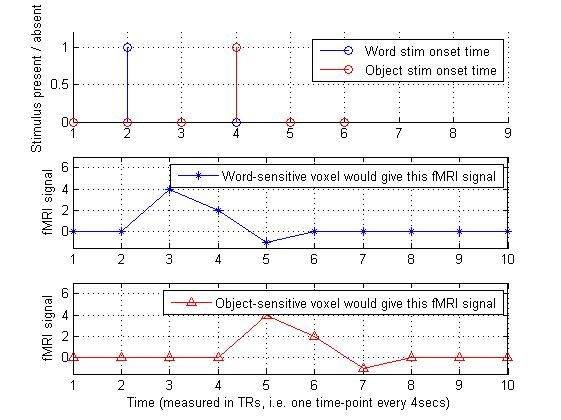
3.利用两个刺激构造设计矩阵,并绘图
predicted_word_response_column_vec = predicted_signal_that_word_would_evoke';
predicted_object_response_column_vec = predicted_signal_that_object_would_evoke';
%%% Now let's look at the actual vectors in the Matlab workspace window
predicted_word_response_column_vec % Because there is no semi-colon after this,
% it will display in workspace window
predicted_object_response_column_vec
%%%%%% Now we can join these two column vectors together
%%%%%% to make the design matrix. We simply put the two columns side-by-side.
%%%%%% In Matlab, you make new matrices and vectors by
%%%%%% putting the contents inside [ square brackets ]
%%%%%% Note that to join them together in this way, they must be
%%%%%% the same length as each other.
%%%%%%
%%%%%% Because the names of my variables are so long and verbose,
%%%%%% the command below spills over onto two lines. In Matlab,
%%%%%% we can split a command over two lines by putting three dots ...
design_matrix = ... % The three dots here mean "continued on the next line"
[ predicted_word_response_column_vec predicted_object_response_column_vec ];
design_matrix % No semi-colon, so it displays in window
%%%%%% Translation guide:
%%%%%% In equations, the design matrix is almost always called X
%%%%%% Note that this is a capital "X".
%%%%%%
%%%%%% X = design_matrix;
%%%%%%
%%%%%% Capitals are typically used for matrices, and small-case is
%%%%%% used for vectors.
%%%%%% The only difference between a vector and a matrix is that
%%%%%% a vector is just a bunch of numbers in a row (a row-vector)
%%%%%% or a bunch of numbers in a column (a column-vector),
%%%%%% whereas a matrix is bunch of vectors stacked up next to each
%%%%%% other to make a rectangular grid, with rows *and* columns of numbers.
%%%%%% Now let's view a grayscale plot of the design matrix,
%%%%%% in the way that an fMRI-analysis package, such as SPM, would show it.
%%%%%% To do this, we use the Matlab command "imagesc".
%%%%%% This takes each number in the design matrix and represents
%%%%%% it as a colour, with the colour depending on how big the number is.
%%%%%% In this case, we'll be using a gray colour-scale, so low numbers
%%%%%% will be shown as darker grays, and high numbers are lighter grays.
%%%%%% The "sc" part at the end of "imagesc" stands for "scale", which
%%%%%% means that Matlab scales the mapping of numbers onto colours so
%%%%%% that the lowest number gets shown as black, and the highest as white.
%%%%%%
%%%%%% For examples of how to use the imagesc command to make
%%%%%% pictures of brain-slices, see the companion program
%%%%%% showing_brain_images_tutorial.m
figure(3);
clf; % Clear the figure
imagesc(design_matrix); % 'imagesc' maps the numbers to colors,
% normalising so that the max goes to white
% and the min goes to black
colormap gray; % Show everything in gray-scale
colorbar; % Shows how the numbers lie on the colour scale
% Note that the highest number in the design matrix,
% which is 4, is shown as white, and the lowest, -1,
% gets shown as black.
title('Gray-scale view of design matrix');
xlabel('Each column represents one stimulus condition');
ylabel('Each row represents one point in time, one row per TR (every 4secs)');

4.设计矩阵和敏感度矩阵相乘,这里假设某一个体素仅仅对某一种刺激有反应,而对另外的刺激没有反应。
%% Now suppose we have a voxel which responds only to words, not to objects.
%% We can calculate how it would be predicted to respond
%% to our word+object display as follows:
%%
%% Predicted response from word-sensitive voxel =
%% 1 * Response which word-presentation would evoke
%% + 0 * Response which object-presentation would evoke
%%
%% Note that this is how the voxel would be predicted to respond
%% if there were no noise whatsoever in the system.
%% Clearly a real fMRI signal would never be this clean.
%%
%% Now, let's make a "sensitivity vector" for this voxel,
%% in which each entry will say how sensitive that voxel is to
%% the corresponding stimulus condition.
%%
%% This voxel is sensitive to words, which are our *first* stimulus-type.
%% And we made the predicted word response into the first column of
%% the design matrix.
%% So, the sensitivity of this voxel to words will be the first element
%% in the sensitivity-vector.
%%
%% Similarly, the sensitivity of this voxel to the second stimulus-type,
%% which are objects, will be the second element in the sensitivity vector.
%%
%% So, the sensitivity vector for a voxel with
%% sensitivity = 1 to the first stimulus-type, which are words
%% and sensitivity = 0 to the second stimulus-type, which are objects
%%
%% will be [ 1 0 ]
%%
%% I know this seems trivial !!
%% Things will get more interesting in a minute...
sensitivity_vec = [ 1 0 ]'; % The dash makes this a column vector
sensitivity_vec % No semi-colon, so it displays in window
%% Translation guide:
%% In equations, the numbers in the sensitivity-vector are typically
%% called "beta-values", or sometimes "beta-coefficients" or "beta-weights".
%% The columns of the design matrix are called "regressors" and
%% the value that is assigned to each regressor is the beta-value.
%%
%% Note that in the example above, we are pretending that we already *know*
%% how sensitive our voxel is to the various stimuli, but in the real world
%% we don't know this. We're trying to figure out what stimuli our voxel
%% is sensitive to, using the fMRI data that we collect in the scanner.
%% This will be described more below.
%% In math-speak, that means that we are trying to *estimate* the betas.
%% When people want to distinguish between the true beta-value
%% (which we don't know) and the estimated beta-value that we figure out
%% from our data, then they call the true one beta and
%% the estimated one "beta hat" (beta with a circumflex sign on top of it: ^
%% [ End of that part of the translation guide, back to the main theme... ]
%% So, we can now express our predicted voxel response in terms
%% of entries in the sensitivity vector multiplied by
%% columns in the design matrix:
%%
%% Predicted response from word-sensitive voxel =
%% 1 * Response which word-presentation would evoke
%% + 0 * Response which object-presentation would evoke
%%
%% And because of the way we made our sensitivity vector and design matrix,
%% this can be re-written as:
%%
%% Predicted response from word-sensitive voxel =
%% (First element in sensitivity vector) * (First column in design matrix)
%% + (Second element in sensitivity vector) * (Second column in design matrix)
%%
%% Here's an important bit:
%% The process above, of going through the elements in a vector,
%% multiplying each element by the corresponding column in a matrix,
%% and then adding up the results of the multiplication,
%% is precisely what matrix multiplication does.
%%
%% In Matlab, everything is by default assumed to be a matrix,
%% (or a vector --- you can think of a vector as simply a matrix that only
%% has one row or column in it), and every multiplication is
%% by default assumed to be a matrix multiplication.
%% So, to matrix-multiply our design matrix by our sensitivity-vector,
%% we just use the standard "multiply by" sign, which is *
predicted_word_selective_voxel_response = design_matrix * sensitivity_vec;
predicted_word_selective_voxel_response
% Let's display this vector in the command window,
% by entering it without a semi-colon after it.
%% When we multiply the design matrix by the sensitivity vector,
%% we make the i-th row of the result by taking the i-th row
%% of the matrix, rotating it 90 degrees, multiplying it element-by-element
%% with the sensitivity vector, and then adding that all up.
%%
%% Since the sensitivity vector is in this case [ 1 0 ],
%% multiplying each matrix row by it element-by-element means that
%% we end up getting 1* the first element in each row, and 0* the second
%% element in each row.
%%
%% So, by the time we have gone through all the rows, we have
%% 1* the first column of the design matrix, plus 0* the second column,
%% which is what we wanted.
%% Let's plot all this
figure(4);
clf; % Clear the figure
subplot(2,1,1); % This is just to make the plots line up prettily
hold on; % "Hold" is one way of putting more than one plot on a figure
h1=plot(predicted_word_response_column_vec,'b*-');
h2=plot(predicted_object_response_column_vec,'r^-');
hold off;
grid on;
legend([h1 h2],'Word-response column vector','Object-response column vector');
axis([1 10 -1.5 7]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
subplot(2,1,2);
plot(predicted_word_selective_voxel_response,'ms-'); % Magenta squares
grid on;
legend('Word-selective voxel-response: 1*word-response + 0*object-response');
axis([1 10 -1.5 7]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
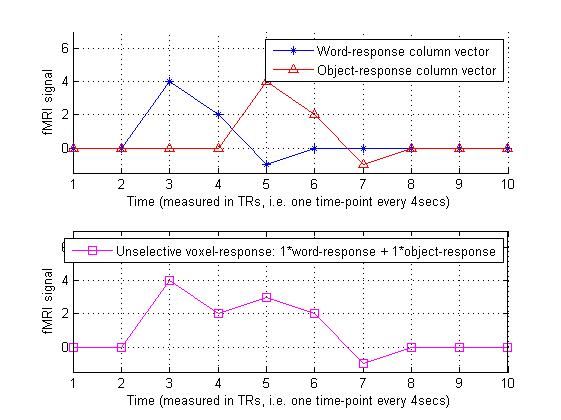
5.假设某一个体素对两种刺激都会产生反应,则它的beta矩阵应当是[1,1]:
%%% Now let's try a voxel which responds equally to both words and objects
%%% So, it's sensitivity vector will be [ 1 1 ]
%%%
%%% This means that its response will be
%%% 1* the first column of the design matrix, plus 1* the second column
%%% i.e.
%%% 1* the response which the word stimulus evokes +
%%% 1* the response which the object stimulus evokes
sensitivity_vec = [ 1 1 ]'; % The dash makes this a column vector
predicted_unselective_voxel_response = design_matrix * sensitivity_vec;
predicted_unselective_voxel_response % Display in Matlab command window
%% Let's plot all this
figure(5);
clf; % Clear the figure
subplot(2,1,1); % This is just to make the plots line up prettily
hold on; % "Hold" is one way of putting more than one plot on a figure
h1=plot(predicted_word_response_column_vec,'b*-');
h2=plot(predicted_object_response_column_vec,'r^-');
hold off;
grid on;
legend([h1 h2],'Word-response column vector','Object-response column vector');
axis([1 10 -1.5 7]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
subplot(2,1,2);
plot(predicted_unselective_voxel_response,'ms-'); % Magenta squares
grid on;
legend('Unselective voxel-response: 1*word-response + 1*object-response');
axis([1 10 -1.5 7]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
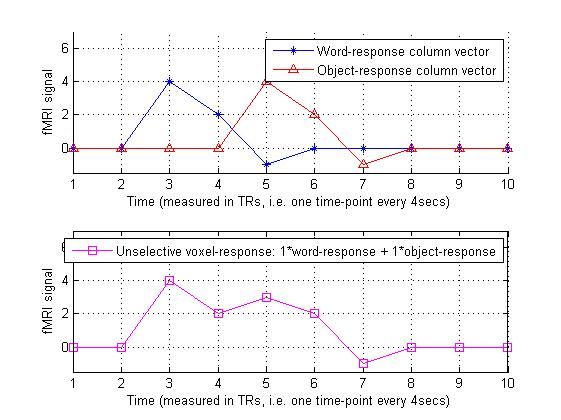
6.假设某一个体素对两种刺激都会产生反应,但是它的beta矩阵是[1,2],即对第二种刺激反应更强烈:
%%% Ok, I hope this isn't overkill: let's try a voxel which gives a normal
%%% response to words, but which gives a response to objects which is
%%% *twice* as strong.
%%% So, it's sensitivity vector will be [ 1 2 ]
%%%
%%% This means that its response will be
%%% 1* the first column of the design matrix, plus 2* the second column
%%% i.e.
%%% 1* the response which the word stimulus evokes +
%%% 2* the response which the object stimulus evokes
sensitivity_vec = [ 1 2 ]'; % The dash makes this a column vector
predicted_object_preferring_voxel_response = design_matrix * sensitivity_vec;
predicted_object_preferring_voxel_response % Display in Matlab command window
%% Let's plot all this
figure(6);
clf; % Clear the figure
subplot(2,1,1); % This is just to make the plots line up prettily
hold on;
h1=plot(predicted_word_response_column_vec,'b*-');
h2=plot(predicted_object_response_column_vec,'r^-');
hold off;
grid on;
legend([h1 h2],'Word-response column vector','Object-response column vector');
axis([1 10 -2 10]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
subplot(2,1,2);
plot(predicted_object_preferring_voxel_response,'ms-'); % Magenta squares
grid on;
legend('Object-preferring voxel-response: 1*word-response + 2*object-response');
axis([1 10 -2 10]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
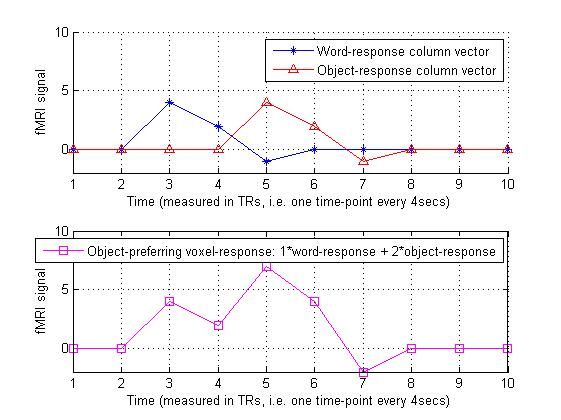
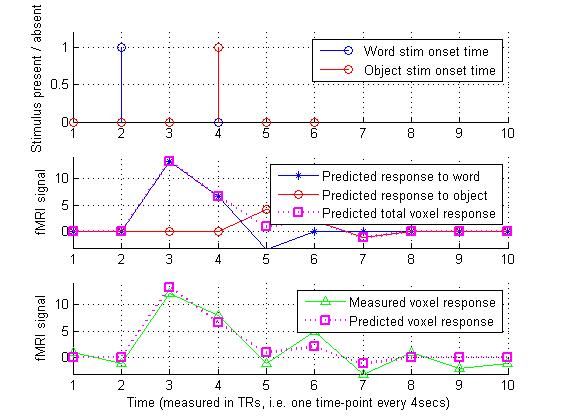
7.我们现在模拟出一个真实测量得到的生理信号体素激活值:
measured_voxel_data = [ 1 -1 12 8 -1 5 -3 1 -2 -1 ]';
% This is is what often gets called "y".
% This measured signal is probably some kind of mixture of
% a response to the word stimulus and a response to the object stimulus,
% with random noise thrown on top.
% Let's plot it
figure(7);
clf; % Clear the figure
plot(measured_voxel_data,'o-');
% Plot HRF against time, with one time-point every TR seconds.
% A line with circles on it
grid on;
xlabel('Time (in units of TRs, 4s long each)');
ylabel('fMRI signal');
title('Measured voxel data');

8.进行数据拟合,矩阵求逆,求伪逆,然后绘图plot,进行比对:
%%% What is the estimated sensitivity vector of this voxel ?
%
% Well, we make the pseudo-inverse of the design matrix, and multiply
% it by the vector of measured voxel data:
estimated_voxel_sensitivity = pinv(design_matrix) * measured_voxel_data;
%%% This estimated_voxel_sensitivity is what gets called beta-hat in the math.
%%% Let's display this in the workspace, by typing it without a semi-colon
estimated_voxel_sensitivity
%%% This makes the following show up in the Matlab command window:
%
% estimated_voxel_sensitivity =
%
% 3.2965
% 1.0565
%
%%% So, the estimate is that this voxel is around 3 times more sensitive to
%%% words than it is to objects
%%% Now, let's make a plot of what the predicted response would be of
%%% a voxel that has a sensitivity matrix which is *exactly* our estimate,
%%% and compare it to the voxel response which we measured.
%%% They won't be exactly the same, because of the noise in the signal.
predicted_voxel_output = design_matrix * estimated_voxel_sensitivity;
%%% This predicted overall voxel output is just the
%%% predicted response to the word, plus the predicted response to the object.
%%% As we saw in hrf_tutorial.m, the idea that we can calculate the overall
%%% response simply by adding up these two separate responses is what it
%%% means to say that we are assuming that the system is LINEAR.
%%%
%%% If we want to look at the predicted responses to the separate stimulus
%%% types, we can calculate them by separately multiplying the
%%% corresponding column of the design matrix by the corresponding element
%%% of the estimated sensitivity vector.
predicted_response_to_word = predicted_word_response_column_vec * ...
estimated_voxel_sensitivity(1);
predicted_response_to_object = predicted_object_response_column_vec * ...
estimated_voxel_sensitivity(2);
%%%%% Let's plot all this
figure(8);
clf; % Clear the figure
subplot(3,1,1); % This is just to make the plots line up prettily
hold on;
h1=stem(word_stim_time_series,'b');
h2=stem(object_stim_time_series,'r'); % Word onset in blue, object onset in red
hold off;
grid on;
legend([h1(1) h2(1)],'Word stim onset time','Object stim onset time');
axis([1 10 0 1.2]); % This just sets the display graph axis size
ylabel('Stimulus present / absent');
subplot(3,1,2);
hold on;
h1=plot(predicted_response_to_word,'b*-');
h2=plot(predicted_response_to_object,'ro-');
h3=plot(predicted_voxel_output,'ms:','linewidth',2);
%%% 'ms:' means plot in the colour magenta (m),
%%% with squares as the markers (s), using a dotted line (:).
%%% Then we make the width of the line broader, linewidth=2,
%%% so that it shows up better.
%%% Note that the predicted_voxel_output is simply the sum of
%%% predicted_response_to_word and predicted_response_to_object
grid on;
legend([h1 h2 h3],'Predicted response to word', ...
'Predicted response to object','Predicted total voxel response');
axis([1 10 -3 14]);
ylabel('fMRI signal');
subplot(3,1,3);
hold on;
h1=plot(measured_voxel_data,'g^-');
h2=plot(predicted_voxel_output,'ms:','linewidth',2);
hold off;
grid on;
legend([h1 h2],'Measured voxel response','Predicted voxel response');
axis([1 10 -3 14]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
%%%% Tutorial on the basic structure of an fMRI design matrix, using Matlab
%%%% Written by Rajeev Raizada, July 23, 2002.
%%%%
%%%% This file follows up on a preceding one: hrf_tutorial.m
%%%%
%%%% Neither file assumes any prior knowledge of linear algebra
%%%%
%%%% Please mail any comments or suggestions to: raizada at cornell dot edu
%%%%
%%%% Probably the best way to look at this program is to read through it
%%%% line by line, and paste each line into the Matlab command window
%%%% in turn. That way, you can see what effect each individual command has.
%%%%
%%%% Alternatively, you can run the program directly by typing
%%%%
%%%% design_matrix_tutorial
%%%%
%%%% into your Matlab command window.
%%%% Do not type ".m" at the end
%%%% If you run the program all at once, all the Figure windows
%%%% will get made at once and will be sitting on top of each other.
%%%% You can move them around to see the ones that are hidden beneath.
%%%%
%%%% Note that this tutorial only shows the method where the
%%%% design matrix assumes a specific shape to the HRF.
%%%% It is also possible to estimate the HRF without making
%%%% any assumptions about its shape. This is called using the
%%%% Finite Impulse Response method, or FIR.
%%%% This involves using a slightly more complicated design-matrix
%%%% than the one we make below.
%%%%
%%%% First, let's make a pretend mini-hrf, just to show examples.
%%%% This is similar in shape to the HRFs that we looked at in
%%%% the program hrf_tutorial.m, but it doesn't have as many time-points.
%%%% One reason to use a shortened HRF like this is just to save typing!
%%%% But in fact, this is approximately what a real HRF would look like
%%%% if you only measured from it once every four seconds.
%%%% In fMRI, the time it takes to make a whole-brain measurement is called
%%%% the TR (Time for Repetition, although people say "Repetition Time").
%%%% So, this HRF is similar to what we'd measure
%%%% if our scanner had a TR of 4 seconds. These days, fast scanners
%%%% can usually manage to get a whole-brain full of data in only 2s.
hrf_small = [ 0 4 2 -1 0 ];
%%%% Plot it
figure(1);
clf; % Clear the figure
plot(0:4,hrf_small,'o-'); % Plot HRF against a time-vector [0,1,2,3,4]
% 'o-' means "use a line with circles on it"
% Type "help plot" in the Matlab command window
% to get a list of all the line-styles and markers
% that you can use. There are lots of them!
grid on; % Overlay a dotted-line grid on top of the plot
xlabel('Time (in units of TRs, 4s long each)');
ylabel('fMRI signal');
title('This is what an HRF would look like if you measure once every 4s')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% Just as we did in hrf_tutorial.m, now we're going to make
% a time-series of 1's and 0's representing the times when stimuli
% are shown. These time-series will be convolved with the HRF,
% in order to see what kinds of fMRI signals would be evoked in voxels
% that respond to the stimuli. These predicted responses will form
% the columns of our design matrix, as is shown in more detail below.
%
% Just for purposes of illustration, we're going to imagine that
% one of our stimuli is flashing up a word on the screen, and that
% the other is flashing up a picture of an object.
%
% These stimulus onsets will probably produce more complex patterns
% of neural firing than the sudden flash of light that we talked about
% in HST_hrf_tutorial.m, but we're going to ignore that complication
% for now. We'll simply suppose that each stimulus instantly kicks off
% its own standard-shaped HRF.
% This is what's typically done in event-related fMRI, and it turns
% out that it usually works pretty well.
%%%%%%%%%%%%%%% Now suppose we present a word at time t=2
word_stim_time_series = [ 0 1 0 0 0 0 ];
%%%%%%%%%%%%%%% And let's present a picture of an object at time t=4
object_stim_time_series= [ 0 0 0 1 0 0 ];
%%%% Let's convolve these with our mini-HRF to see what kind of fMRI
%%%% signals they would evoke in voxels which respond to words or pictures
predicted_signal_that_word_would_evoke = conv(word_stim_time_series,hrf_small);
predicted_signal_that_object_would_evoke = conv(object_stim_time_series,hrf_small);
%%% Let's plot all this
figure(2);
clf; % Clear the figure
subplot(3,1,1); % This is just to make the plots line up prettily.
% The first number is how many rows of subplots we have: 3
% The second number is how many columns: 1
% The third number is which subplot to draw in: the first one.
% So, we end up with three plots stacked on top of each other,
% and we draw in the first one (which is the uppermost subplot)
hold on; % "Hold" is one way of putting more than one plot on a figure
h1=stem(word_stim_time_series,'b');
% Stem makes a nice looking plot with lines and circles
h2=stem(object_stim_time_series,'r'); % Word onset in blue, object onset in red
% The "h1=" and "h2=" bits are called "handles".
% They are pointers to the plots that we are making,
% which are the stem plots in this case.
% Making handles like this is useful for manipulating
% pretty much any aspect of the plot afterwards.
% In this instance, we use them to put a legend on the plot.
% That's done by the "legend" command, a couple of lines below.
% There's no need to worry about these handles at this stage,
% I just wanted to explain what those mysterious-looking h's
% were doing there. Usually you can make a nice-looking legend
% without worrying about handles, but it turns out that
% for stem plots they help to make the legend look better.
hold off;
grid on;
legend([h1(1) h2(1)],'Word stim onset time','Object stim onset time');
% We use the h1 and h2 handles here.
% This helps us to get the right symbols displayed in the legend,
% in this case, blue and red circles.
axis([1 9 0 1.2]); % This just sets the display graph axis size
% The first two numbers are the x-axis range: 1 to 9
% The last two numbers are the y-axis range: 0 to 1.2
ylabel('Stimulus present / absent');
subplot(3,1,2);
plot(predicted_signal_that_word_would_evoke,'b*-');
% 'b*-' means blue stars on a solid line
grid on;
legend('Word-sensitive voxel would give this fMRI signal');
axis([1 10 -1.5 7]);
ylabel('fMRI signal');
subplot(3,1,3);
plot(predicted_signal_that_object_would_evoke,'r^-');
% 'r^-' means red triangles
% pointing up, lying on a solid line.
grid on;
legend('Object-sensitive voxel would give this fMRI signal');
axis([1 10 -1.5 7]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%
%%%%%% What the design matrix has in it
%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%
%%%%%% Here's the key part.
%%%%%% The design matrix is built up out of these predicted responses.
%%%%%%
%%%%%% Each column of the design matrix is the predicted fMRI signal
%%%%%% that a voxel would give, if it were perfectly and exclusively
%%%%%% sensitive to a particular stimulus-condition.
%%%%%%
%%%%%% In our case, the first column of the design matrix
%%%%%% would be the vector "predicted_signal_that_word_would_evoke"
%%%%%% that we made just above, and the second column would be
%%%%%% the vector "predicted_signal_that_object_would_evoke"
%%%%%%
%%%%%% So, the most important part of the design matrix
%%%%%% is simply these two vectors side-by-side.
%%%%%%
%%%%%% A real design matrix would have some other columns in it too,
%%%%%% which have other types of predicted fMRI signals in them,
%%%%%% e.g. what the signal would look like if the scanner's output
%%%%%% were slowly drifting in time.
%%%%%% But those other columns don't deal with the signal that the stimuli
%%%%%% would be predicted to evoke in the brain, and so we can ignore them
%%%%%% for now. (Later in the HST583 course, Doug will talk more about
%%%%%% how you might model slow-scanner drift etc.)
%%%%%%
%%%%%% It's the *columns* of the design matrix that get built up out of
%%%%%% these predicted responses to the different stimulus types,
%%%%%% but the actual vectors that we made above are row vectors,
%%%%%% i.e. just a bunch of numbers in a row.
%%%%%% So, to match the format of the design matrix, we need to turn
%%%%%% these into column vectors, by transposing them (i.e. flipping them).
%%%%%% We do this by putting a dash/apostrophe at the end of the vector
predicted_word_response_column_vec = predicted_signal_that_word_would_evoke';
predicted_object_response_column_vec = predicted_signal_that_object_would_evoke';
%%% Now let's look at the actual vectors in the Matlab workspace window
predicted_word_response_column_vec % Because there is no semi-colon after this,
% it will display in workspace window
predicted_object_response_column_vec
%%%%%% Now we can join these two column vectors together
%%%%%% to make the design matrix. We simply put the two columns side-by-side.
%%%%%% In Matlab, you make new matrices and vectors by
%%%%%% putting the contents inside [ square brackets ]
%%%%%% Note that to join them together in this way, they must be
%%%%%% the same length as each other.
%%%%%%
%%%%%% Because the names of my variables are so long and verbose,
%%%%%% the command below spills over onto two lines. In Matlab,
%%%%%% we can split a command over two lines by putting three dots ...
design_matrix = ... % The three dots here mean "continued on the next line"
[ predicted_word_response_column_vec predicted_object_response_column_vec ];
design_matrix % No semi-colon, so it displays in window
%%%%%% Translation guide:
%%%%%% In equations, the design matrix is almost always called X
%%%%%% Note that this is a capital "X".
%%%%%%
%%%%%% X = design_matrix;
%%%%%%
%%%%%% Capitals are typically used for matrices, and small-case is
%%%%%% used for vectors.
%%%%%% The only difference between a vector and a matrix is that
%%%%%% a vector is just a bunch of numbers in a row (a row-vector)
%%%%%% or a bunch of numbers in a column (a column-vector),
%%%%%% whereas a matrix is bunch of vectors stacked up next to each
%%%%%% other to make a rectangular grid, with rows *and* columns of numbers.
%%%%%% Now let's view a grayscale plot of the design matrix,
%%%%%% in the way that an fMRI-analysis package, such as SPM, would show it.
%%%%%% To do this, we use the Matlab command "imagesc".
%%%%%% This takes each number in the design matrix and represents
%%%%%% it as a colour, with the colour depending on how big the number is.
%%%%%% In this case, we'll be using a gray colour-scale, so low numbers
%%%%%% will be shown as darker grays, and high numbers are lighter grays.
%%%%%% The "sc" part at the end of "imagesc" stands for "scale", which
%%%%%% means that Matlab scales the mapping of numbers onto colours so
%%%%%% that the lowest number gets shown as black, and the highest as white.
%%%%%%
%%%%%% For examples of how to use the imagesc command to make
%%%%%% pictures of brain-slices, see the companion program
%%%%%% showing_brain_images_tutorial.m
figure(3);
clf; % Clear the figure
imagesc(design_matrix); % 'imagesc' maps the numbers to colors,
% normalising so that the max goes to white
% and the min goes to black
colormap gray; % Show everything in gray-scale
colorbar; % Shows how the numbers lie on the colour scale
% Note that the highest number in the design matrix,
% which is 4, is shown as white, and the lowest, -1,
% gets shown as black.
title('Gray-scale view of design matrix');
xlabel('Each column represents one stimulus condition');
ylabel('Each row represents one point in time, one row per TR (every 4secs)');
%% Now suppose we have a voxel which responds only to words, not to objects.
%% We can calculate how it would be predicted to respond
%% to our word+object display as follows:
%%
%% Predicted response from word-sensitive voxel =
%% 1 * Response which word-presentation would evoke
%% + 0 * Response which object-presentation would evoke
%%
%% Note that this is how the voxel would be predicted to respond
%% if there were no noise whatsoever in the system.
%% Clearly a real fMRI signal would never be this clean.
%%
%% Now, let's make a "sensitivity vector" for this voxel,
%% in which each entry will say how sensitive that voxel is to
%% the corresponding stimulus condition.
%%
%% This voxel is sensitive to words, which are our *first* stimulus-type.
%% And we made the predicted word response into the first column of
%% the design matrix.
%% So, the sensitivity of this voxel to words will be the first element
%% in the sensitivity-vector.
%%
%% Similarly, the sensitivity of this voxel to the second stimulus-type,
%% which are objects, will be the second element in the sensitivity vector.
%%
%% So, the sensitivity vector for a voxel with
%% sensitivity = 1 to the first stimulus-type, which are words
%% and sensitivity = 0 to the second stimulus-type, which are objects
%%
%% will be [ 1 0 ]
%%
%% I know this seems trivial !!
%% Things will get more interesting in a minute...
sensitivity_vec = [ 1 0 ]'; % The dash makes this a column vector
sensitivity_vec % No semi-colon, so it displays in window
%% Translation guide:
%% In equations, the numbers in the sensitivity-vector are typically
%% called "beta-values", or sometimes "beta-coefficients" or "beta-weights".
%% The columns of the design matrix are called "regressors" and
%% the value that is assigned to each regressor is the beta-value.
%%
%% Note that in the example above, we are pretending that we already *know*
%% how sensitive our voxel is to the various stimuli, but in the real world
%% we don't know this. We're trying to figure out what stimuli our voxel
%% is sensitive to, using the fMRI data that we collect in the scanner.
%% This will be described more below.
%% In math-speak, that means that we are trying to *estimate* the betas.
%% When people want to distinguish between the true beta-value
%% (which we don't know) and the estimated beta-value that we figure out
%% from our data, then they call the true one beta and
%% the estimated one "beta hat" (beta with a circumflex sign on top of it: ^
%% [ End of that part of the translation guide, back to the main theme... ]
%% So, we can now express our predicted voxel response in terms
%% of entries in the sensitivity vector multiplied by
%% columns in the design matrix:
%%
%% Predicted response from word-sensitive voxel =
%% 1 * Response which word-presentation would evoke
%% + 0 * Response which object-presentation would evoke
%%
%% And because of the way we made our sensitivity vector and design matrix,
%% this can be re-written as:
%%
%% Predicted response from word-sensitive voxel =
%% (First element in sensitivity vector) * (First column in design matrix)
%% + (Second element in sensitivity vector) * (Second column in design matrix)
%%
%% Here's an important bit:
%% The process above, of going through the elements in a vector,
%% multiplying each element by the corresponding column in a matrix,
%% and then adding up the results of the multiplication,
%% is precisely what matrix multiplication does.
%%
%% In Matlab, everything is by default assumed to be a matrix,
%% (or a vector --- you can think of a vector as simply a matrix that only
%% has one row or column in it), and every multiplication is
%% by default assumed to be a matrix multiplication.
%% So, to matrix-multiply our design matrix by our sensitivity-vector,
%% we just use the standard "multiply by" sign, which is *
predicted_word_selective_voxel_response = design_matrix * sensitivity_vec;
predicted_word_selective_voxel_response
% Let's display this vector in the command window,
% by entering it without a semi-colon after it.
%% When we multiply the design matrix by the sensitivity vector,
%% we make the i-th row of the result by taking the i-th row
%% of the matrix, rotating it 90 degrees, multiplying it element-by-element
%% with the sensitivity vector, and then adding that all up.
%%
%% Since the sensitivity vector is in this case [ 1 0 ],
%% multiplying each matrix row by it element-by-element means that
%% we end up getting 1* the first element in each row, and 0* the second
%% element in each row.
%%
%% So, by the time we have gone through all the rows, we have
%% 1* the first column of the design matrix, plus 0* the second column,
%% which is what we wanted.
%% Let's plot all this
figure(4);
clf; % Clear the figure
subplot(2,1,1); % This is just to make the plots line up prettily
hold on; % "Hold" is one way of putting more than one plot on a figure
h1=plot(predicted_word_response_column_vec,'b*-');
h2=plot(predicted_object_response_column_vec,'r^-');
hold off;
grid on;
legend([h1 h2],'Word-response column vector','Object-response column vector');
axis([1 10 -1.5 7]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
subplot(2,1,2);
plot(predicted_word_selective_voxel_response,'ms-'); % Magenta squares
grid on;
legend('Word-selective voxel-response: 1*word-response + 0*object-response');
axis([1 10 -1.5 7]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
%%% Now let's try a voxel which responds equally to both words and objects
%%% So, it's sensitivity vector will be [ 1 1 ]
%%%
%%% This means that its response will be
%%% 1* the first column of the design matrix, plus 1* the second column
%%% i.e.
%%% 1* the response which the word stimulus evokes +
%%% 1* the response which the object stimulus evokes
sensitivity_vec = [ 1 1 ]'; % The dash makes this a column vector
predicted_unselective_voxel_response = design_matrix * sensitivity_vec;
predicted_unselective_voxel_response % Display in Matlab command window
%% Let's plot all this
figure(5);
clf; % Clear the figure
subplot(2,1,1); % This is just to make the plots line up prettily
hold on; % "Hold" is one way of putting more than one plot on a figure
h1=plot(predicted_word_response_column_vec,'b*-');
h2=plot(predicted_object_response_column_vec,'r^-');
hold off;
grid on;
legend([h1 h2],'Word-response column vector','Object-response column vector');
axis([1 10 -1.5 7]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
subplot(2,1,2);
plot(predicted_unselective_voxel_response,'ms-'); % Magenta squares
grid on;
legend('Unselective voxel-response: 1*word-response + 1*object-response');
axis([1 10 -1.5 7]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
%%% Ok, I hope this isn't overkill: let's try a voxel which gives a normal
%%% response to words, but which gives a response to objects which is
%%% *twice* as strong.
%%% So, it's sensitivity vector will be [ 1 2 ]
%%%
%%% This means that its response will be
%%% 1* the first column of the design matrix, plus 2* the second column
%%% i.e.
%%% 1* the response which the word stimulus evokes +
%%% 2* the response which the object stimulus evokes
sensitivity_vec = [ 1 2 ]'; % The dash makes this a column vector
predicted_object_preferring_voxel_response = design_matrix * sensitivity_vec;
predicted_object_preferring_voxel_response % Display in Matlab command window
%% Let's plot all this
figure(6);
clf; % Clear the figure
subplot(2,1,1); % This is just to make the plots line up prettily
hold on;
h1=plot(predicted_word_response_column_vec,'b*-');
h2=plot(predicted_object_response_column_vec,'r^-');
hold off;
grid on;
legend([h1 h2],'Word-response column vector','Object-response column vector');
axis([1 10 -2 10]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
subplot(2,1,2);
plot(predicted_object_preferring_voxel_response,'ms-'); % Magenta squares
grid on;
legend('Object-preferring voxel-response: 1*word-response + 2*object-response');
axis([1 10 -2 10]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% So, to recap:
%
% Voxel response = Design matrix * sensitivity vector
%
% Each column of the design matrix is the response to a particular stimulus.
% Each row of it is a moment in time, with one row per MRI image-acquisition.
% So, reading down a column (through the rows), gives the response through
% time to a particular stimulus.
%
% Each element in the sensitivity vector is a measure of how much that voxel
% responds to the stimulus in the corresponding column of the design matrix.
%
% When we multiply the design matrix by the sensitivity vector, this produces a
% result which takes each column, which is the responses that each stimulus-type
% would evoke, then multiplies that column by how sensitive that voxel is to
% that particular stimulus, and then adds together the results of all
% those multiplications.
%
% But so far we've only been talking about an imaginary situation
% in which we already *know* which stimuli our voxel is sensitive to, and we use
% that knowledge to calculate how the voxel ought to respond.
% That's why we have been talking about *predicted* voxel responses so far.
%
% Here's the key bit: in fMRI, we have exactly the reverse situation:
% we *measure* how the voxels respond, and we want to figure out which
% stimuli they must therefore have been sensitive to.
%
% ie. Voxel response = Design matrix * sensitivity vector
%
% ^ ^ ^
% | | |
% We measure this We build this We want to find this out
% with the scanner from stimulus This is what the analysis works out
% onset times
%
%
% So, we measure a voxel's response, and we know that it should be
% equal to (Design matrix * sensitivity vector)
% It won't be exactly equal to that, because the signal is noisy.
% We'll ignore the noise for now, but we'll come back to it soon below.
%
% What we need to do is to unpack the result of this multiplication,
% so that we can take (Design matrix * sensitivity vector)
% and pull out the part that we don't already know and that we want,
% namely the sensitivity vector.
%
% To do that, we need the concept of a MATRIX INVERSE.
%
% If multiplying by a matrix, M, does one thing,
% then multiplying by its inverse, inv(M), does the opposite.
%
% From above, we know the value of Design matrix * sensitivity vector
%
% (its value is the voxel response), but what we need to find out
% is just the sensitivity vector on its own.
%
% So, we can achieve this by multiplying by the inverse of the design matrix
%
% inv(design matrix) * design matrix * sensitivity vector
%
% = sensitivity vector
%
%
% But since design matrix * sensitivity vector = voxel response,
%
% the above is the same as:
%
% inv(design matrix) * voxel response
%
% Given that we *know* the design matrix (we built it), we just need
% to calculate its inverse, multiply it by the voxel response, and
% then we will get that voxel's sensitivity vector.
%
% sensitivity vector = inv(design matrix) * voxel response
%
% And since the voxel's sensitivity vector is just a list of the
% responses which it gives to each of the stimuli which we presented,
% it therefore tells us which stimuli make that voxel light up.
%
% And that is what we wanted to find out!
%
% This is pretty much what any fMRI-analysis package does,
% although they often organise the results a bit differently.
% The "sensitivity vector" above is a list of numbers for a single voxel:
% each number describes how closely the BOLD signal time-course from that
% voxel matches to the corresponding column of the design matrix.
%
% In an fMRI-analysis package, instead of getting a separate
% "sensitivity vector" for each voxel, you may instead get
% a "sensitivity image" for each design matrix column,
% where each image is a brain-full of sensitivity values.
% Since these sensitivity values are called "betas", the
% brains-full of beta-values are called "beta-images".
% The value in a given voxel is the measure of how closely
% that voxel's BOLD time-course matches to the
% corresponding column of the design matrix.
% In SPM, for example, beta_001.img is a brain-full of numbers
% saying how sensitive each voxel is to the 1st column in the
% design matrix. So, the beta-images are made up of the same
% numbers as we are calculating here for the "sensitivity vector",
% it's just that they're grouped into brain-sized images,
% rather than given one voxel at a time.
%
% Now, it turns out that what I just told you about inverses
% isn't really true. We don't multiply by the inverse of the design matrix.
% We multiply by something that is basically the same, only slightly
% more complicated, called the "pseudo-inverse".
% In Matlab, the pseudo-inverse of X is written pinv(X).
%
% If you really want to know, pinv(X) = inv(X'*X)*X'
%
% This isn't a really important difference.
% The key point is to see that trying to figure out a voxel's sensitivity
% vector is the problem of trying to work out which vector would have to be
% multiplied by the design matrix, in order to give the voxel response vector
% which we measured with the scanner.
%
% So, the equation for figuring out a voxel's sensitivity is:
%
% Voxel response = Design matrix * sensitivity vector
%
% which means that we can calculate the sensitivity vector like this:
%
% Sensitivity vector = pinv(design matrix) * voxel response
%
% We mentioned above that there's noise in the signal.
% It turns out that
% With the noise included, the equation is:
%
% Voxel response = Design matrix * sensitivity vector + noise
%
% ... where noise means
% "anything in the measured signal that our design matrix can't explain".
%
% This is a problem, because with the noise, it's no longer true
% that the measured voxel response is exactly equal to the
% design matrix multiplied by the sensitivity vector.
% Luckily, it turns out that this doesn't stop us from being able
% to *estimate* a sensitivity vector, even though the noise prevents us
% from being able to calculate exactly what the voxel's sensitivities are.
% It turns out that we can still use the pseudo-inverse of the design matrix,
% and that this gives us the best estimate of the sensitivity vector that
% we could get, despite the noise.
%
% So, although the noise prevents us from calculating the "true" sensitivity
% vector, it doesn't stop us from getting a good estimate:
%
% estimated sensitivity vector = pinv(design matrix) * voxel response
%
% Translation guide:
% The fMRI signal that we measure from the scanner, which
% we call "voxel response" or "measured_voxel_data" here, is
% usually called "y" in equations.
%
% As before, the design matrix is called X, and the
% voxel sensitivities are called beta-values.
% To show that a beta-value is estimated, rather than being the real but
% unknown sensitivity of the voxel, a hat sign gets put on it: beta-hat
%
% So, instead of the equation that we write below:
% estimated_voxel_sensitivity = pinv(design_matrix) * measured_voxel_data;
%
% .. you'll see an equation that looks like this:
%
% beta = inv(X'*X)*X' * y;
%
% or, with the hat-sign to show that beta is just an estimate:
%
% beta_hat = inv(X'*X)*X' * y;
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Ok, let's try that with an example.
%
% Suppose we measure this data:
measured_voxel_data = [ 1 -1 12 8 -1 5 -3 1 -2 -1 ]';
% This is is what often gets called "y".
% This measured signal is probably some kind of mixture of
% a response to the word stimulus and a response to the object stimulus,
% with random noise thrown on top.
% Let's plot it
figure(7);
clf; % Clear the figure
plot(measured_voxel_data,'o-');
% Plot HRF against time, with one time-point every TR seconds.
% A line with circles on it
grid on;
xlabel('Time (in units of TRs, 4s long each)');
ylabel('fMRI signal');
title('Measured voxel data');
%%% What is the estimated sensitivity vector of this voxel ?
%
% Well, we make the pseudo-inverse of the design matrix, and multiply
% it by the vector of measured voxel data:
estimated_voxel_sensitivity = pinv(design_matrix) * measured_voxel_data;
%%% This estimated_voxel_sensitivity is what gets called beta-hat in the math.
%%% Let's display this in the workspace, by typing it without a semi-colon
estimated_voxel_sensitivity
%%% This makes the following show up in the Matlab command window:
%
% estimated_voxel_sensitivity =
%
% 3.2965
% 1.0565
%
%%% So, the estimate is that this voxel is around 3 times more sensitive to
%%% words than it is to objects
%%% Now, let's make a plot of what the predicted response would be of
%%% a voxel that has a sensitivity matrix which is *exactly* our estimate,
%%% and compare it to the voxel response which we measured.
%%% They won't be exactly the same, because of the noise in the signal.
predicted_voxel_output = design_matrix * estimated_voxel_sensitivity;
%%% This predicted overall voxel output is just the
%%% predicted response to the word, plus the predicted response to the object.
%%% As we saw in hrf_tutorial.m, the idea that we can calculate the overall
%%% response simply by adding up these two separate responses is what it
%%% means to say that we are assuming that the system is LINEAR.
%%%
%%% If we want to look at the predicted responses to the separate stimulus
%%% types, we can calculate them by separately multiplying the
%%% corresponding column of the design matrix by the corresponding element
%%% of the estimated sensitivity vector.
predicted_response_to_word = predicted_word_response_column_vec * ...
estimated_voxel_sensitivity(1);
predicted_response_to_object = predicted_object_response_column_vec * ...
estimated_voxel_sensitivity(2);
%%%%% Let's plot all this
figure(8);
clf; % Clear the figure
subplot(3,1,1); % This is just to make the plots line up prettily
hold on;
h1=stem(word_stim_time_series,'b');
h2=stem(object_stim_time_series,'r'); % Word onset in blue, object onset in red
hold off;
grid on;
legend([h1(1) h2(1)],'Word stim onset time','Object stim onset time');
axis([1 10 0 1.2]); % This just sets the display graph axis size
ylabel('Stimulus present / absent');
subplot(3,1,2);
hold on;
h1=plot(predicted_response_to_word,'b*-');
h2=plot(predicted_response_to_object,'ro-');
h3=plot(predicted_voxel_output,'ms:','linewidth',2);
%%% 'ms:' means plot in the colour magenta (m),
%%% with squares as the markers (s), using a dotted line (:).
%%% Then we make the width of the line broader, linewidth=2,
%%% so that it shows up better.
%%% Note that the predicted_voxel_output is simply the sum of
%%% predicted_response_to_word and predicted_response_to_object
grid on;
legend([h1 h2 h3],'Predicted response to word', ...
'Predicted response to object','Predicted total voxel response');
axis([1 10 -3 14]);
ylabel('fMRI signal');
subplot(3,1,3);
hold on;
h1=plot(measured_voxel_data,'g^-');
h2=plot(predicted_voxel_output,'ms:','linewidth',2);
hold off;
grid on;
legend([h1 h2],'Measured voxel response','Predicted voxel response');
axis([1 10 -3 14]);
xlabel('Time (measured in TRs, i.e. one time-point every 4secs)');
ylabel('fMRI signal');
%%%%%% From Fig.8, we can see that the voxel-sensitivities that we estimated
%%%%%% give a predicted overall voxel response which matches reasonably
%%%%%% closely to the actual measured voxel data.
%%%%%%
%%%%%% But the match isn't perfect.
%%%%%% That's because the MRI signal has noise in it.
%%%%%% By "noise", we basically mean, "any changes in the MRI signal that
%%%%%% our design matrix can't explain".
%%%%%%
%%%%%% All that our design matrix talks about is the predicted response
%%%%%% to the word stimulus and the predicted response to the object stimulus.
%%%%%% These predicted responses are made from HRFs, and so they change
%%%%%% on a slow, HRF kind of time-scale, i.e. over several seconds.
%%%%%%
%%%%%% So, if there are either much more rapid changes in the fMRI signal,
%%%%%% or much slower changes, then the design matrix won't be able to
%%%%%% account for them.
%%%%%%
%%%%%% In a real design matrix, there would be extra columns that would
%%%%%% try to account for any slower changes that there might be,
%%%%%% e.g. slow drifts in the signal that the scanner is giving out.
%%%%%%
%%%%%% Sometimes it's also possible to explain away very rapid changes.
%%%%%% For example, if we put columns in the design matrix that describe
%%%%%% how much the subject's head moved, then it might turn out
%%%%%% that some of the rapid MRI signal changes correlate closely with
%%%%%% the amount of head-movement. This is what people are referring to
%%%%%% when they talk about "putting in motion as a regressor".
%%%%%%
%%%%%% But there's always some noise that we simply can't get rid of.
%%%%%% If there's not much left-over noise, then we can be fairly
%%%%%% confident that the voxel-sensitivity vector that we calculated above
%%%%%% is a good estimate.
%%%%%% And if there's a lot of left over noise, then we probably won't
%%%%%% be very confident.
%%%%%%
%%%%%% That's the basis of the statistical tests that
%%%%%% any fMRI-analysis package starts to apply after it has
%%%%%% used the design matrix to estimate how sensitive each voxel is
%%%%%% to the various stimulus-types that we presented.
%%%%%%
%%%%%% However, those statistical tests are a topic for a different talk.
%%%%%%
%%%%%% A couple of good websites to check out, which also have
%%%%%% accompanying Matlab code, are these ones by Matthew Brett:
%%%%%% http://www.mrc-cbu.cam.ac.uk/Imaging/spmstats.html
%%%%%% http://www.mrc-cbu.cam.ac.uk/Imaging/statstalk.m
%%%%%%
%%%%%% and also several programs by Russ Poldrack, which are listed here:
%%%%%% http://www.nmr.mgh.harvard.edu/~poldrack/spm/tutorials/