数字图像处理学习笔记（十二）——频率域滤波

数字图像处理(Digital Image Processing)是通过计算机对图像进行去除噪声、增强、复原、分割、提取特征等处理的方法和技术。本专栏将以学习笔记形式对数字图像处理的重点基础知识进行总结整理，欢迎大家一起学习交流！
 专栏链接：数字图像处理学习笔记

滤波器：抑制或最小化某些频率的波和震荡的装置或材料
              低通滤波器抑制或最小化高频率的波
              高通滤波器抑制或最小化低频率的波
频率：自变量单位变化期间内，一个周期函数重复相同值序列的次数

在数字图像处理中，有两个经典的变换被广泛应用——傅里叶变换和霍夫变换。
其中，傅里叶变换主要是将时间域上的信号转变为频率域上的信号，用来进行图像除噪、图像增强等处理。

图像傅里叶变换原理

傅里叶变换（Fourier Transform，简称FT）常用于数字信号处理
它的目的是将时间域上的信号转变为频率域上的信号。
随着域的不同，对同一个事物的了解角度也随之改变，因此在时域中某些不好处理的地方，在频域就可以较为简单的处理。同时，可以从频域里发现一些原先不易察觉的特征。
傅里叶定理指出“任何连续周期信号都可以表示成（或者无限逼近）一系列正弦信号的叠加”。

时间域与频率域转换对比
时间域角度

频率域角度
             

绘制对应的时间图和频率图

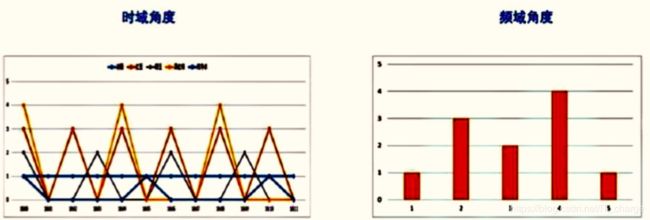横轴代表时间                                                                    横轴代表频率的倒数

傅里叶公式

将时间域的函数表示为频率域的函数f(t)的积分
一维图像的傅里叶变换公式：
注：w表示频率，t表示时间，为复变函数。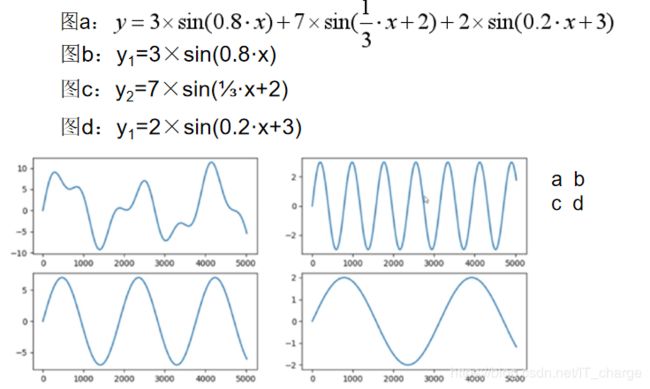

二维图像的傅里叶变换公式
                                            
注：f是空间域（Spatial Domain）)值，F是频域（Frequency Domain）值

傅里叶变换可以应用于图像处理中，经过对图像进行变换得到其频谱图。
从谱频图里频率高低来表征图像中灰度变化剧烈程度。
图像中的边缘信号和噪声信号往往是高频信号，而图像变化频繁的图像轮廓及背景等信号往往是低频信号。
这时可以有针对性的对图像进行相关操作，例如图像除噪、图像增强和锐化等。

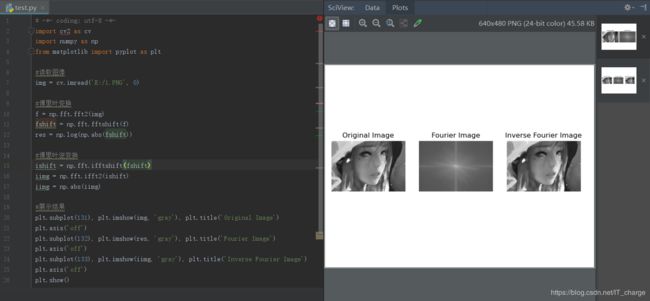
Numpy实现傅里叶变换及逆变换

Numpy中的 FFT包提供了函数 np.fft.fft2()可以对信号进行快速傅里叶变换
函数原型：fft2(a, s=None, axes=(-2, -1), norm=None)
注：a表示输入图像
       s表示整数序列，可以决定输出数组的大小
       axes表示整数序列，用于计算FFT的可选轴
       norm包括None和ortho两个选项

OpenCV实现傅里叶变换及逆变换

在OpenCV 中，通过函数cv2.idft()实现傅里叶逆变换
和用Numpy输出的结果一样，但与Numpy实现不同的是，OpenCV输出结果是双通道的
第一个通道是结果的实数部分，第二个通道是结果的虚数部分，并且输入图像要首先转换成 np.float32 格式
实现傅里叶变换函数原型：dst = cv2.dft(src, dst=None, flags=None, nonzeroRows=None)
注：src表示输入图像，需要通过np.float32转换格式
       dst表示输出图像，包括输出大小和尺寸
       flags表示转换标记
由于输出的频谱结果是一个复数，需要调用cv2.magnitude()函数将傅里叶变换的双通道结果转换为0到255的范围。
将傅里叶变换双通道转换2到255函数原型：cv2.magnitude(x, y)
注：x表示浮点型X坐标值，即实部
       y表示浮点型Y坐标值，即虚部
最终输出结果为幅值，即：
实现傅里叶逆变换函数原型：dst = cv2.idft(src[, dst[, flags[, nonzeroRows]]])
注：src表示输入图像，包括实数或复数
       dst表示输出图像
       flags表示转换标记
        nonzeroRows表示要处理的dst行数

傅里叶变换的目的并不是为了观察图像的频率分布，更多情况下是为了对频率进行过滤，通过修改频率以达到图像增强、图像去噪、边缘检测、特征提取、压缩加密等目的。
过滤的方法一般有三种：低通（Low-pass）、高通（High-pass）、带通（Band-pass）。
低通就是保留图像中的低频成分，过滤高频成分
高通就是保留图像中的高频成分，过滤低频成分

高通滤波

高通滤波器是指通过高频的滤波器，衰减低频而通过高频
常用于增强尖锐的细节（提取边缘轮廓），但会导致图像的对比度会降低。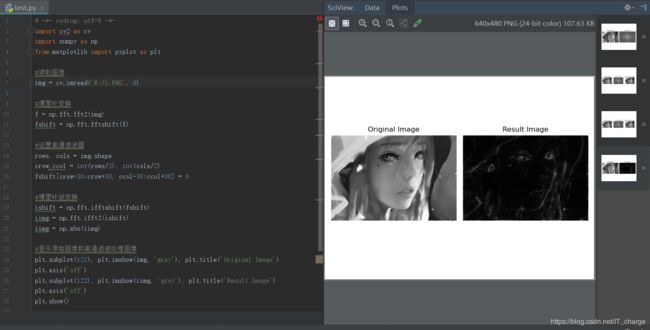

低通滤波

低通滤波器是指通过低频的滤波器，衰减高频而通过低频
常用于模糊图像或对图像去噪（因为噪声是高频的）

图中第14行代码数值越小模糊程度越大，是因为数值越小保留区域越小，所以数值越小越模糊。

 

上述实验用到的频谱图像中心区域为低频部分，其余地方为高频部分

 

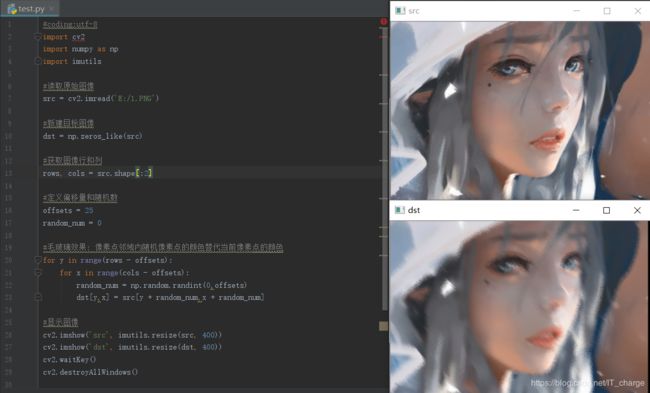
图像毛玻璃特效

它是用图像邻域内随机一个像素点的颜色来替代当前像素点颜色的过程，从而为图像增加一个毛玻璃模糊的特效。

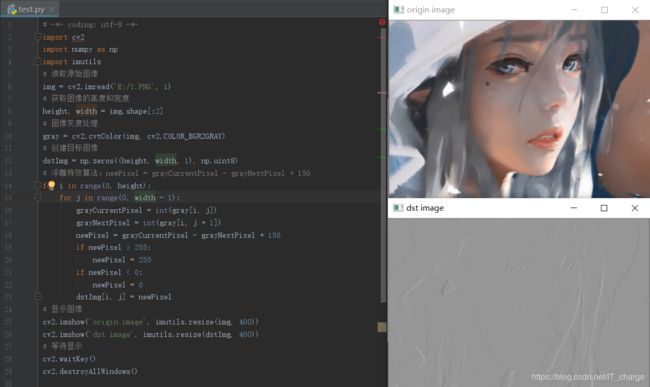
图像浮雕特效

Python绘制浮雕图像是通过勾画图像的轮廓，并降低周围的像素值，从而产生一张具有立体感的浮雕效果图

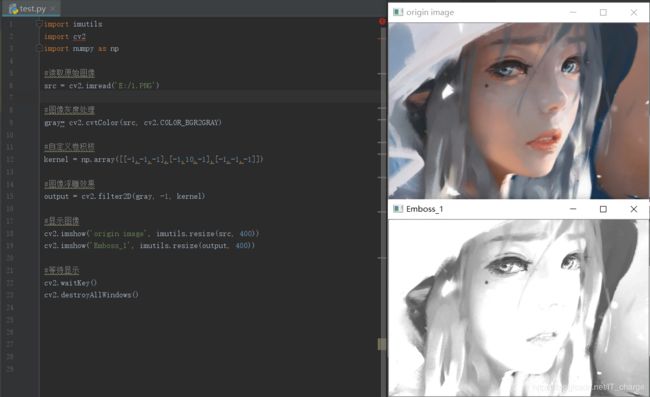
图像油漆特效

图像油漆特效主要采用自定义卷积核和cv2.filter2D()函数实现，Python实现代码主要通过Numpy定义卷积核，再进行特效处理

 

---

欢迎留言，一起学习交流~~~

感谢阅读

END