机器学习笔记
有监督学习与无监督学习
有目标变量的研究,称为有监督学习,常用于预测未来。
无目标变量的研究,称为无监督学习,常用于描述现在。
根据具体问题和算法不同,常常分为以下六小类:
- 分类 Classification(有监督学习)
- 回归 Regression(有监督学习)
- 异常检测 Deviation Detection(有监督学习)
- 聚类 Clustering(无监督学习)
- 关联规则 Association Rule Discovery(无监督学习)
- 序列挖掘 Sequential Pattern Discovery(无监督学习)
一般挖掘流程
问题理解
首先是清晰地定义问题和目标其次是评估现有条件。根据资源和约束、判断挖掘项目的可行性制定初步规划和分析思路,将问题分解分解映射到后续的多个数据挖掘步骤中
数据理解
数据准备
数据建模
模型评价
模型部署
聚类
聚类目的是捕获数据的自然结构,从而将数据自动划分为有意义的几个组群,这些组群的特点在于组内的变异较小,而组间的变异较大。聚类分析还可以用来探索数据的结构,还可以用来对数据进行预处理,为进一步的数据挖掘工作起到压缩和降维的作用。
层次聚类
又称为系统聚类。聚类首先要清晰地定义样本之间的距离关系,远近为不同类。
过程: 首先将每个样本单独作为一类,然后将不同类之间的距离最近的进行合并,合并后重新计算类间距。这个过程一直持续到将所有样本归为一类为止。
6种距离计算方法: 最短距离法、最长距离法、类平均法、重心法、中间距离法、离差平方和法。
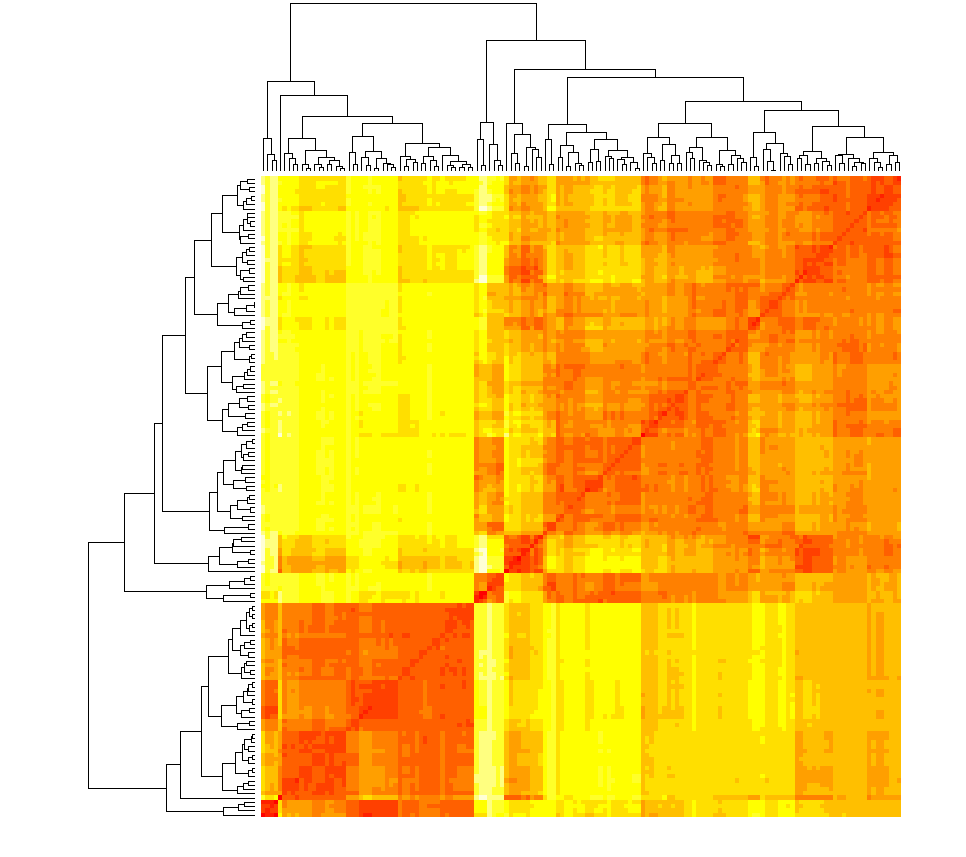
stats包hclust函数重要参数:样本的距离矩阵,及计算类间距离的方法。下面使用iris数据集来进行层次聚类分析,首先提取iris数据中的4个数值变量,标准化之后计算其欧式距离矩阵。
data <- iris[,-5]
means <- sapply(data, mean); SD <- sapply(data, sd)
scaledata <- scale(data, means, SD)
Dist <- dist(scaledata, method = 'euclidean')
然后根据矩阵绘制热图。从图可看到,颜色越深表示样本间距越近,大致上可以区分出三到四个区块,其样本之间距离比较接近。
heatmap(as.matrix(Dist), labRow = F, labCol = F)
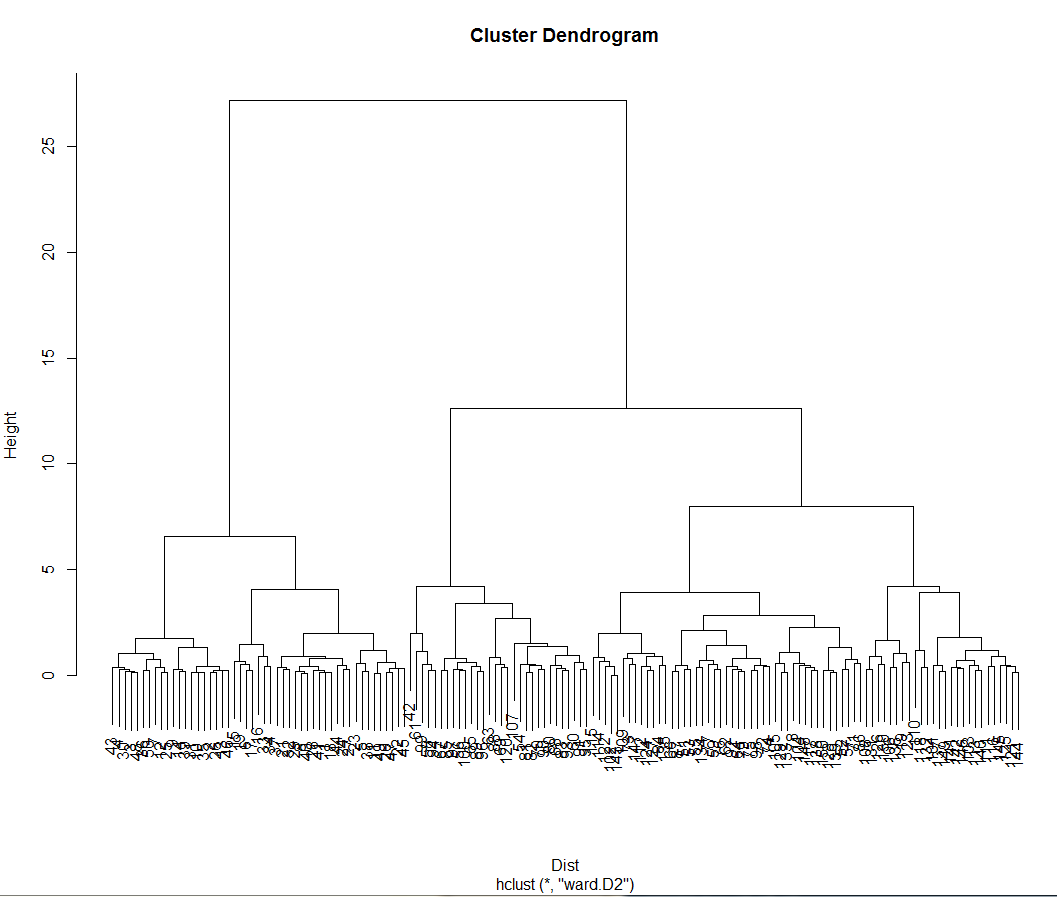
最后使用hclust函数建立聚类模型,结果存在clusteModel变量中,其中ward参数是将类间距离计算方法设置为离差平方和法。如果我们希望将类别设为3类,可以使用cutree函数提取每个样本所属的类别。观察真实的类别和聚类之间的差别,发现virginica类错分了23个样本
clustemodel <- hclust(Dist, method = 'ward.D2')
result <- cutree(clustemodel, k=3)
table(iris[,5], result) **观察聚类和真实的分类对比**
> table(iris[,5], result)
1 2 3
setosa 49 1 0
versicolor 0 27 23
virginica 0 2 48
plot(clustemodel) **聚类树图**
层次聚类的特点是:基于距离矩阵进行聚类,不需要原始数据。可用于不同形状的聚类,但它对于异常点比较敏感,对于数据规模较小的数据比较合适,否则计算量会相当大,聚类前无需确定聚类个数,之后切分组数可根据业务知识,也可以根据聚类树图的特征。
如果样本量很大,可以尝试用fastcluster包进行快速层次聚类。包加载之后,其hclust函数会覆盖同名函数,参数和方法都一样。
library(fastcluster)
clustemodel <- hclust(Dist, method = "ward.D2")
聚类需要将距离矩阵作为输入,所以聚类的关键是距离计算方法的选择,这种选择会极大的影响聚类的结果,而这种选择往往依赖于具体的应用场景。可用于定义“距离”的度量方法包括了常见的欧式距离(euclidean)、曼哈顿距离(manhattan)、两项距离(binary)、闵可夫斯基(minkowski),以及更为抽象的相关系数和夹角余弦等。另外如果特征的量纲不一,还需要考虑适当的标准化和转换方法,或者使用马氏距离。用户也可以输入自定义的距离矩阵。
常规的距离可以通过dist函数得到,其他一些特殊的距离可以加载proxy包。例如余弦距离。
library(proxy)
res <- dist(data,method = 'cosine')
前面计算距离时处理的均为数值变量,如果是二分类变量,可采用杰卡德(Jaccard)方法计算它们之间的距离。例如,x和y样本各有6个特征加以描述,二者取1的交集合个数为3,取1的并集合个数为5,因此相似程度为3/5,那么二者之间的距离可以认为是2/5。
> res <- dist(data,method = 'cosine')
> x <- c(0,0,1,1,1,1)
> y <- c(1,0,1,1,0,1)
> dist(rbind(x,y), method = 'Jaccard')
x
y 0.4
如果是处理多个取值的分类变量,可以将其转为多个二分类变量,其方法和线性回归中将因子变量转为哑变量是一样的作法。
还有一种特殊情况的距离计算,就是分类变量和数值变量混合在一起的情况。下例的两个样本中的第3和5个特征为数值变量,其他为二分类变量,另外还有一个缺失值。我们可以先用离差计算单个特征的距离,再进行合并计算。
x <- c(0,0,1.2,1,0.5,1,NA)
y <- c(1,0,2.3,1,0.9,1,1)
d <- abs(x-y)
dist <- sum(d[!is.na(d)])/6
K均值聚类
K均值聚类又称为动态聚类,它的计算方法快速简便。首先要指定聚类的分类个数N,先随机取K个点作为初始的类中心或者说是质心。计算个样本点与类中心的距离并就近归类。所有样本归类完成后,重新计算类中心,重复迭代这个过程直到类中心不再变化。
使用kmeans函数进行K均值聚类,重要参数如下:
x: 设置要聚类的数据对象,并非距离矩阵。
centers: 用来设置分类个数。
nstart: 用来设置取随机初始中心的次数,其默认值为1,取较多的次数可以改善聚类效果。
下面仍是使用标准化后的iris数据集来聚类,之后提取每个样本所属的类别。
clustemodel <- kmeans(dataScale, centers = 3, nstart = 10)
class(clustemodel)
K均值聚类计算仍然要考虑距离,这里kmeans函数缺省使用欧式距离来计算,如果需要使用其他距离定义,可以采用cluster包中的pam函数,配合proxy包来计算。例如下面我们使用了马氏距离。
library(proxy)
library(cluster)
clustmodel <- pam(dataScale, k = 3, metric = 'Mahalanobis')
clustmodel$medoids
table(iris$Species, clustmodel$clustering)
下两图显示了两项轮廓系数图和主成分散点图以观察聚类效果。轮廓图中各样本点的条状长度为silhouette值,值越大表示聚类效果越好,值越小标书此样本位于两个类的边缘交界地带。
par(mfcol = c(1 ,2))
plot(clustmodel, which.plots = 2, main = '')
plot(clustmodel, which.plots = 1, main = '')
kmeans函数和pam函数略有区别,kmeans的类中心不属于原数据中的某个样本,而pam的类中心是数据中的某一个样本,其区别类似于均值和中位数之间的差别。
使用K均值聚类时需要注意,最初的类中心是通过随机生成的,这样有时可能会形成较差的聚类结果。
改进的方法包括:多次尝试聚类;抽样后先使用层次聚类确定初始中心;选择比较大的K值聚类,之后手工合并相近的类;或着是采用两分法K均值聚类。
K均值聚类要求事先给出分类个数K。K值可以根据业务知识加以确定,或者先用层次聚类已决定个数。改善聚类的方法还包括对原始数据进行变换,例如对数据降维后再聚类。聚类效果可以参考轮廓系数加以判断,轮廓系数(silhouette coefficient)方法考虑了组内的凝聚度和组间的分离度,以此来判断聚类的优良性,其值在-1到+1之间取值,值越大表示效果越好。
rinds提供了一个自定义的简单函数bestCluster,输入数据和一个整数向量,可以自动输出轮廓系数最优的聚类数:
rinds::bestCluster(dataScale, 2:6)
## [1] 2
上面的函数判断类别数位2是最优聚类。fpc包中的kmeansruns函数也可以自动探测最佳的聚类数。下例中轮廓系数最大的0.68对应的正是两个聚类。
library(pfc)
pka <- kmeansruns(iris[, 1:4], krange = 2:6,
critout = TRUE, runs = 2,
criterion = 'asw')
k均值聚类方法快速简单,但它不适合非球形的数据,对异常值也比较敏感。cluster扩展包中也有许多函数可用于其他方式的聚类分析,如agnes函数可用于凝聚层次聚类,diana可用于划分层次聚类,fanny用于模糊聚类。
基于密度的聚类
k均值聚类的缺点在于它不能识别非球形的蔟。我们可以用一个简单的例子来观察k均值聚类的弱点。
基于sin和cos函数构造两组人工数据
x1 <- seq(0,pi,length.out = 100)
y1 <- sin(x1) +0.1*rnorm(100)
x2 <- 1.5 +seq(0, pi, length.out = 100)
y2 <- cos(x2) + 0.1*rnorm(100)
data <- data.frame(c(x1, x2), c(y1, y2))
names(data) <- c('x','y')
model1 <- kmeans(data, centers = 2, nstart = 10)
如下图,不同的类用不同的颜色表示,观察到其聚类结果是不理想的,因为它不能识别非球形的蔟。
为了解决这个问题,我们可以使用DBSCAN方法,它是一种基于密度的聚类方法。它寻找哪些被低密度区域所分离的高密度区域。DBSCAN方法的重要概念如下:
核心点:如果某个点的领域内的点的个数超过某个阈值,则他是一个核心点,即表示它位于蔟的内部。领域的大小由半径参数eps决定。阈值由MiniPts参数决定。
边界点:如果某个点不是核心点,但它落在核心点的领域内,则它是边界点。
噪声点:非核心点也非边界点。
简单来讲,DBSCAN的算法是将所有点标记为核心点,边界点或噪声点,将任意两个距离小于eps的核心点归为同一个蔟。任何与核心点足够近的边界点也放到与之相同的蔟中。
应用fpc包中的dbscan函数可以实施密度聚类。重要参数如下:
eps:定义领域的半径大小。
MinPts:定义阈值以判断核心点。
噪声点:非核心点也非边界点。
下面实施密度聚类,其中eps参数设为0.3,即两个点之间距离小于0.3则归为一簇,而阈值MinPts设为4,若某点的领域中有4个点以上,则该点定义为核心点。
library('fpc')
model2 <- dbscan(data,eps =0.3, MinPts = 4)
从上图中可以看到DBSCAN方法很好地划分了两个蔟。其中要注意参数eps的设置,如果eps设置过大,则所有的点都会归为一个蔟,设置过小,那么蔟的数目会过多。如果MinPts设置过大的话,很多点将被视为噪声点。
可以看到基于密度聚类的优良特性,它可以对抗噪声,能处理任何形状和大小的蔟,这样可以发现K均值不能发现的蔟。但是对于高维数据,点之间极为稀疏,密度就很难定义了。而这种算法对于计算资源的消耗也是很大的。
自组织映射
自组织映射SOM不仅是一种聚类的技术,也是一种降维可视化的技术。
前面介绍的降维技术,PCA是为了保留原有数据的变异,MDS是为了保留原有数据的距离,而至于SOM,它是为了保留原有数据的拓扑结构,或者说邻居间的关系。SOM是将高维空间中的邻居,投影到二维网络中。这个二维网络通常是矩形或六边形。
SOM计算方法类似于在空间约束下的K均值聚类,二维网格的节点个数现决定了聚类数目。一开始先给节点赋初始值,随后样本数据逐个和节点比较距离,距离最近的某些节点值将会得到调整更新。这种比较的顺序是随机的,而距离的计算可以是欧式距离或是点积。节点更新将会受到两个参数的影响,一个是学习速率alpha,另一个是领域影响范围radius。这种比较和更新的过程持续迭代,一直到节点值收敛到一个稳定值。
kohonen包可以实施多种SOM算法,其中重要的参数包括
分类
预处理
set.seed(1)
data(PimaIndiansDiabetes2, package = “mlbench”)
data <- PimaIndiansDiabetes2
library(caret)
标准化处理
preProcValues <- preProcess(data[, -9],
method = c(‘center’, ‘scale’))
scaleddate <- predict(preProcValues, data[, -9])
YeoJohnson转换,使数据接近正态分布,并减弱异常值的影响
preProcbox <- preProcess(scaleddate,
method = c(‘YeoJohnson’))
boxdata <- predict(preProcbox, scaleddate)
缺失值插补,装袋算法
preProcimp <- preProcess(boxdata, method = ‘bagImpute’)
procdata <- predict(preProcimp, boxdata)
procdata$class <- data[,9]
决策树模型
特点:
是一种简单易用的非参数分类器。不需要对数据有任何先验假设,计算速度较快,结果容易解释,而且稳健性很强,对噪声数据和缺失数据不敏感。
分类回归树方法(CART):
是众多树模型算法中的一种,它先从n个变量中寻找最佳分割变量和最佳分割点,将数据划分为两组。针对分组后的数据将上述步骤重复下去,直到满足某种停止条件。这样反复分割数据后使分组后的数据变得一致,纯度较高。同时可自动探测出复杂数据的潜在结构/重要模式和关系。
树模型分为分类树(classification tree)和回归树(regression tree)两种。分类树用于因变量为分类数据的情况,树的末端为因变量的分类值;回归树则可以用于因变量为连续变量的情况,树的末端可以给出相应类别中的因变量描述或预测。
建树模型的三个步骤:
第一步是对所有自变量和所有分割点进行评估,最佳的选择是使分割后组内的数据纯度更高,即组内数据的目标变量变异更小。这种纯度可以通过Gini值或是熵Entropy来度量。
第二步是对树进行修剪。如若不修剪加以限制,模型会产生“过度拟合”的问题,这样的模型在实际应用中毫无意义,而从另一个极端情况来看,若树的枝节太少,那么必然也会带来很大的预测误差。综合来看,要兼顾树的规模和误差的大小,因此通常会使用CP参数(complexity parameter)来对树的复杂度进行控制,使预测误差和树的规模都尽可能的小。CP参数类似于岭回归中的惩罚系数,数字越小模型越偏向于过度拟合。通常做法是先建立一个划分较细较为复杂的树模型,再根据交叉检验(cross-validation)方法来估计不同“剪枝”条件下各模型的误差,选择误差最小的树模型。
第三步是输出最终结果,进行预测和解释。
rpartb包可实现CART算法,其中重要的参数是cp,它由control进行控制。设置cp参数为0,是为了让模型变得复杂,以方便后面演示剪枝处理。
library(caret)
library(rpart)
rpartmodel <- rpart(class~., data = procdata,
control = rpart.control(cp=0))
预测误差是由xerror表示,即交叉检验的模型预测误差。我们可以寻找最小xerro值对应的cp值,并由此cp值决定树的大小。根据上面的输出自动求出对应最小的cp值,再用prune函数对树模型进行修剪。
cptable <- as.data.frame(rpartmodel$cptable)
cptable$errsd <- cptable$xerror + cptable$xstd
cpvalue <- cptable[which.min(cptable$errsd),"CP"]
prunemodel <- prune(rpartmodel, cpvalue)
剪枝后的模型存到prunemodel对象中,使用rpart.plot包来画出决策树结构图(划分变量和阈值)
library(rpart.plot)
rpart.plot(prunemodel)
rpart模型运行快速,不怕缺失和冗余变量,解释性强,但缺点在于:因为它是矩形的判别边界,使得精确度不高,对回归问题不太适合。
处理回归问题时建议使用模型树(model tree)方法,即先将数据切分,再对各组数据进行线性回归。party包中的mob函数和RWeka包中的M5P函数可以建立模型树。
另一个缺点在于,单个决策树不太稳定,数据微小的变化会造成模型结构变化。树模型还会有变量选择偏向,即会选择那些有取值较多的变量。一种改善的做法是使用条件推断树,即party包中的ctree函数,还可以采用集成学习法,例如随机森林算法。
效果的衡量:以决策树为例
统计模型可以直接从各项检验的结果判断模型的好坏。但是数据挖掘和机器学习这类算法模型通常解释性没有这么强,而算法模型通常都是为了预测,那么一个很现实的解决办法就是通过比较真实值和预测值之间的差异来衡量模型的效果。
构建表格来评价二元分类器的预测效果。所有训练数据都会落入这两行两列的表格中,对角线上的数字代表了预测正确的数目,同时可以相应算出TPR(真正率或灵敏度)和TNR(真负率或特异度),这个表格称为混淆矩阵(confusion matrix)
pre <- predict(prunemodel,procdata, type = 'class')
(pretable <- table(pre, procdata$class))
pre neg pos
neg 442 116
pos 58 152
(accuracy <- sum(diag(pretable))/sum(pretable)) *diag 取矩阵对角数据*
[1] 0.7734375
上表的纵轴是预测值,横轴是真实值,落在对角线上的数字为预测正确的样本。
灵敏度,即在真实为阴性条件下预测正确的比率;
特异度,在真实为阳性条件下预测正确的比率。
pretable[1,1]/sum(pretable[,1]) #灵敏度
[1] 0.884
pretable[2,2]/sum(pretable[,2]) #特异度
[1] 0.5671642
看到58例本来没病,被误诊为有病;116例本来是有病,被误诊为无病。这两类错判的意义不同,成本可能也是不一样的。本着宁可错杀不可放过的思路,可以在建模函数中增加成本矩阵的参数设置,将未诊断出有病的成本增加到5倍,这样使模型的特异度增加到0.96,但牺牲了灵敏度,而且总体准确率也下降了。
> rpartmodel <- rpart(class~., data = procdata,
control = rpart.control(cp=0.01),
parms = list(loss=matrix(c(0,5,1,0),2)))
> pre <- predict(rpartmodel, procdata, type = 'class')
> pretable <- table(pre, procdata$class)
> (accuracy <- sum(diag(pretable))/sum(pretable))
[1] 0.6914062
> pretable[1,1]/sum(pretable[, 1])
[1] 0.55
> pretable[2,2]/sum(pretable[, 2])
[1] 0.9552239
注意既用它训练,又用它进行预测,这容易导致过度拟合(overfit),往往会高估模型的准确性。
处理过度拟合的思路:
其一是保留数据,例如多重交叉检验;
其二是用正则化方法对模型的复杂度进行约束,例如岭回归(ridge regression)和套索方法(LASSO)
衡量模型效果最常用的方法是多重交叉检验(cross-validation)。以十重交叉检验为例,将数据随机分为十组,第一次训练对象是1~9组,检验对象是第10组,第二次训练是2~10组,检验对象第1组,然后依次轮换。如果还需要调参,一种典型的做法就是先将数据划分为训练集合检验集。训练集中用多重交叉检验来选择调校模型,参数确定后使用整体训练集得到最终模型,再用检验集来观察判断最终模型的效果。
这里使用准确率为度量指标,将数据切分为十份,使用循环分别建模10次,观察结果。
num <- sample(1:10, nrow(procdata), replace = T)
res <- array(0, dim = c(2,2,10))
n <- ncol(procdata)
for (i in 1:10) {
train <- procdata[num!=i,]
test <- procdata[num==i,]
model <- rpart(class~., data = train,
control = rpart.control(cp=0.1))
pre <- predict(model, test[, -n], type = 'class')
res[,,i] <- as.matrix(table(pre,test[, n]))
}
table <- apply(res, MARGIN=c(1,2),sum)
sum(diag(table))/sum(table)
经过10重交叉检验,可以认为消除了单次建模的偶然性,那么模型的准确率实际上应该是0.75,可见和之前的0.86有较大差距。
也可以直接用caret包的train函数来建模并自动实施10重交叉检验。给定一个参数,进行一次10重交叉检验会得到一个模型的结果,我们输入10个不同的CP参数,分别进行交叉检验可以得到10个对应的结果。
library(e1071)
table <- apply(res, MARGIN=c(1,2),sum)
sum(diag(table))/sum(table)
fitcontrol <- trainControl(method = 'repeatedcv',
number = 10, repeats = 3)
tunedf <- data.frame(.cp = seq(0.001, 0.1, length = 10))
treemodel <- train(x = procdata[, -9], y = procdata[, 9],
method = 'rpart', trControl = fitcontrol, tuneGrid = tunedf)
plot(treemodel)
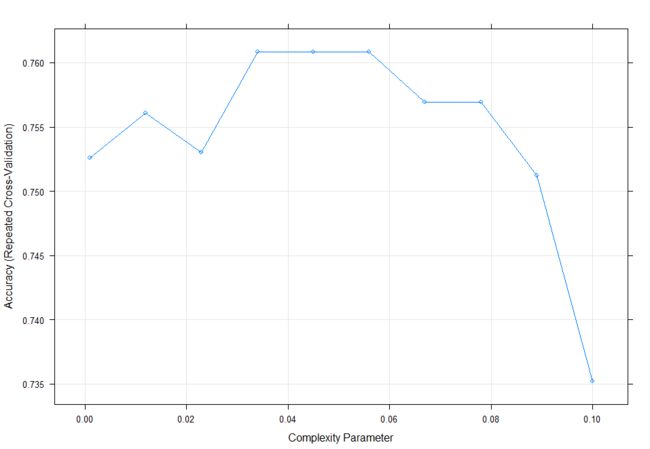
先使用trainControl设置检验的控制参数,确定为10重交叉检验,反复进行3次。目的是为了减少模型评价的不稳定性,这样得到30次检验结果。在参数调校中,确定CP参数从0.001开始,到0.1结束。训练时使用模型为rpart建模函数。用10个不同的参数来进行交叉检验。
如图,可以看到,CP参数在0.045附近可以得到最优的预测准确率,我们可以用这个参数对整个训练集或者是对未来的新数据进行预测。caret包中的predict.train函数会自动选择最优参数,并对整个训练集进行一次预测。
贝叶斯分类
朴素贝叶斯分类(naive bayes classifier)是一种简单而容易理解的分类方法,看起来很朴素,但用起来却很有效。背后的原理就是贝叶斯定理,即先赋予目标变量一个先验概率,再根据数据中的新的信息,对先验概率进行更新,从而得到后验概率。
klaR包中的NaiveBayes函数,该函数可以输入先验概率,另外在正态分布基础上增加了核平滑密度函数。为了避免过度拟合,在训练时还要将数据分割进行多重检验,所以还要使用carat包的一些函数进行配合。
NaiveBayes最重要的两个参数:
usekernel: 确定是否使用核密度平滑,如果选择否,则使用正态分布。
fL: 设置平滑系数,这是为了防止某个后验概率计算为0的结果。
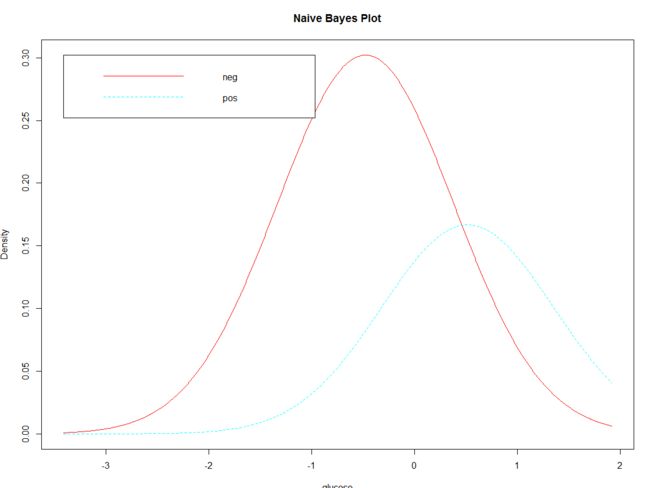
我们使用该函数建模并通过图形查看变量glucose的影响:
library(klaR)
nbmodel <- NaiveBayes(class~., data = procdata,
usekernel = FALSE, fL = 1)
plot(nbmodel, vars = 'glucose', legendplot = T)
从图可以观察到不同变量对于因变量的影响,例如葡萄糖浓度越高,患病概率越大。
我们可以直接使用caret包来实施朴素贝叶斯分类,并进行多重交叉检验:
fitcontrol <- trainControl(method = 'repeatedcv',
number = 10, repeats = 3)
nbmodel <- train(x = procdata[, -9], y = procdata[, 9],
method = 'nb', trControl = fitcontrol,
tuneGrid = data.frame(.fL = 1, .usekernel = TRUE, adjust = T))
densityplot(nbmodel)
经过三次10重交叉检验,可以看到,其准确率在0.75左右,用户也可以使用nbmodel$resample调出具体结果数据。
最邻近分类(kth Nearest Neighbor)KNN
如果我们已经拥有一些已知类别的数据,要对一些未知类别的数据进行分类,基本思路就是将数据看作实在多元空间中的点。先计算未知点的类别。例如设k为3,对某个未知点找出其周围最近的三个已知点,如果这三个点有两个属于A类,一个属于B类,那么根据多数原则,将未知点的类别预测为A类。
**优势:**KNN算法的优势在于算法简单,稳健性强,可以构成非线性的判别边界,模型参数简单,只有距离测度和k参数。其弱点在于计算量较大,对异常点和不平衡数据都较为敏感。
class包的knn函数可以实行基本的KNN算法,其参数即是近邻个数k。
使用caret包来调校参数,找出最优的k值:
library(caret)
fitcontrol <- trainControl(method = 'repeatedcv',
number = 10, repeats = 3)
tunedf <- data.frame(.k = seq(3,20,by=2))
knnmodel <- train(x = procdata[, -9], y = procdata[, 9],
method = 'knn', trControl = fitcontrol,
tuneGrid = tunedf)
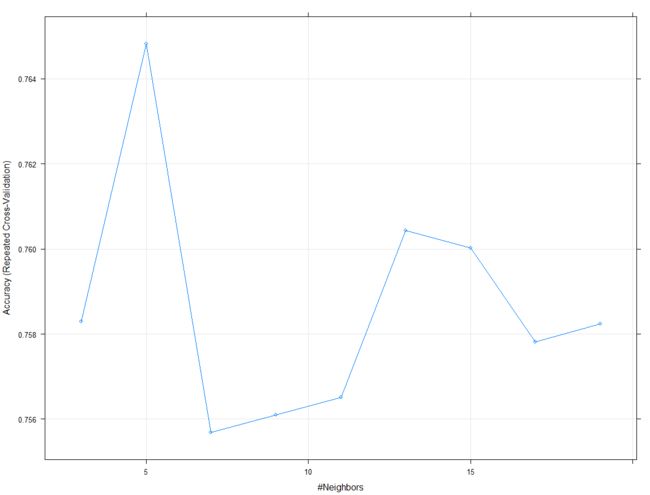
plot(knnmodel)
由图可见,K取13的时候,模型预测准确率最高。
对于KNN算法,R语言中另外还有一个kknn包值得关注,它对于基本的knn函数有很大程度的扩展。他可以结合核函数,利用距离进行加权计算。
神经网络分类
BP神经网络分类是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。
BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。
BP神经网络模型拓扑结构包括输入层、隐层(hide layer)和输出层。对于分类问题,BP神经网络类似于集合了多个logistic回归函数,每个神经元都由一个函数负责计算,前面一层函数的输出将成为后面一层函数的输入。
nnet包可以实现BP神经网络分类算法,其中的重要参数有:
size: 隐层神经元个数,数字越大模型越复杂。
decay: 学习速率,是为了避免过度拟合问题,这个值一般在0到0.1之间。
linout: 隐层到输出层的函数形式,若是回归问题则设置为TRUE,表示线性输出,若是分类问题则设置为FALSE,表示非线性输出。
caret包中的avNNet函数对nnet包有所改进,它使用同一个BP神经网络模型,而是用不同的初始随机种子,最后预测时进行综合预测。这样可以一定程度上避免模型训练时陷入局部最优解。
library(caret)
fitcontrol <- trainControl(method = 'repeatedcv',
number = 10, repeats = 3)
tunedf <- expand.grid(.decay=0.1, .size = 5:10, .bag = TRUE)
nnetmodel <- train(class~., data = procdata,
method = 'avNNet',trControl = fitcontrol,
trace = FALSE, linout = FALSE, tuneGrid = tunedf)
plot(nnetmodel)
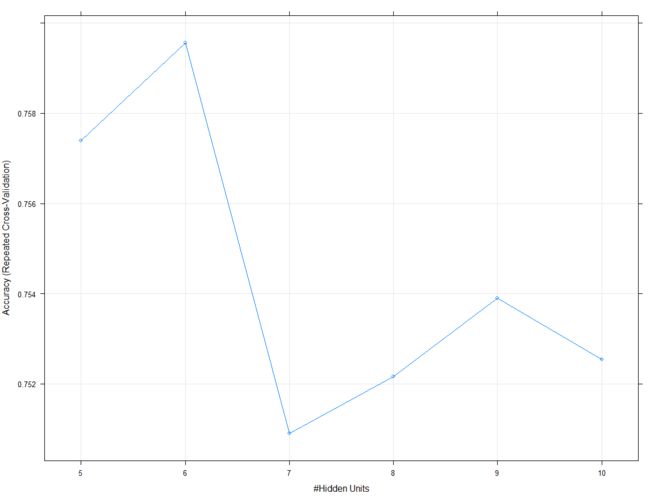
上面我们控制decay参数为常值,这是为了避免调校参数过多,计算时间过长。上面的结果显示BP神经网络模型的参数在隐层神经元为6个时,准确率最高。
BP神经网络的特点是可以拟合任何一种函数,容易陷入局部极值,导致过度拟合,而且计算量大。一种解决方法是在数据预处理时使用PCA,在train函数的method中使用pcaNNet即可直接实施基于PCA的神经网络。但它可以处理冗余变量,因为冗余变量的权重在学习训练中会变得很小。
支持向量机分类
支持向量机(Support Vector Machine, SVM)是以统计学理论为基础,它不仅结构简单,而且技术性能明显提高。理解SVM有四个关键概念:分离超平面、最大边缘超平面、软边缘、核函数。
分离超平面(separation hyperplane):处理分类问题的时候需要一个决策边界,好像楚河汉界一样,在界这边我们判别A,在界那边我们判别B。这种决策边界将两类事物相分离,而线性的决策边界就是分离超平面。
最大边缘超平面(maximal margin hyperplane):分离超平面可以有很多个,SVM的作法是找一个“最中间”的。换句话说,就是这个平面要尽量和两边保持距离,以留足余量,减小泛化误差,保证稳健性。在数学上找到这个最大边缘超平面的方法是一个二次规划问题。
软边缘(soft margin):但很多情况下样本点不会乖乖地分开两边站好,都是“你中有我,我中有你“的混沌状态。不大可能用一个平面完美分离两个类别。在线性不可分的情况下就要考虑软边缘了。软边缘可以破例允许个别样本跑到其他类别的地盘上去。但要使用参数来权衡两端,一个是要保持最大边缘的分离,另一个要使这种破例不能太离谱。这种参数就是对错误分类的惩罚程度C。
核函数(kernel function): 为了解决完美分离的问题,SVM还提出一种思路,就是将原始数据映射到高维空间去,直觉上可以感觉高维空间中的数据变得稀疏,有利于分清“敌我”。那么映射的方法就是使用“核函数”。如果这种“核技术”选择得当,高维空间中的数据就变得容易线性分离了。
而且可以证明,总是存在一种核函数能将数据集映射成可分离的高维数据。但是映射到高维空间中并非是有百利而无一害的,维数过高的害处就是出现过度拟合。
所以选择合适的核函数以及软边缘参数C就是训练SVM的重要因素。一般来讲,核函数越复杂,模型越偏向于拟合过度,反之则拟合不足。实践中仍然是使用我们常用的交叉检验来确定参数。
常用的核函数有如下种类:
Linear:线性核函数,使用它的花就称为线性向量机,效果基本等价于Logistic回归。但它可以处理变量极多的情况,例如文本挖掘。
polynomial:多项式核函数,适用于图像处理问题。
Radial basis:高斯核函数,最流行易用的选择。参数包括了sigma,其值若设置过小,会有过度拟合出现,但这个参数也可以自动计算出最优值。
sigmoid:反曲核函数,多用于神经网络的激活函数。
R语言中可以用e1071包中的svm函数建模,而另一个kernlab包中则包括了更多的核方法函数,我们主要使用其中的ksvm函数,来说明参数C的作用和核函数的选择。
我们使用人为构造的一个线性不可分割的数据集LMdata作为例子,该数据包含在rinds包中,专门用来测试SVM的算法。首先使用线性核函数来建模,其参数C取值为0.1:
data(LMdata, package = 'rinds')
library(kernlab)
model1 <- ksvm(y~., data = LMdata$SVM,
kernel = 'vanilladot', C = 0.1)
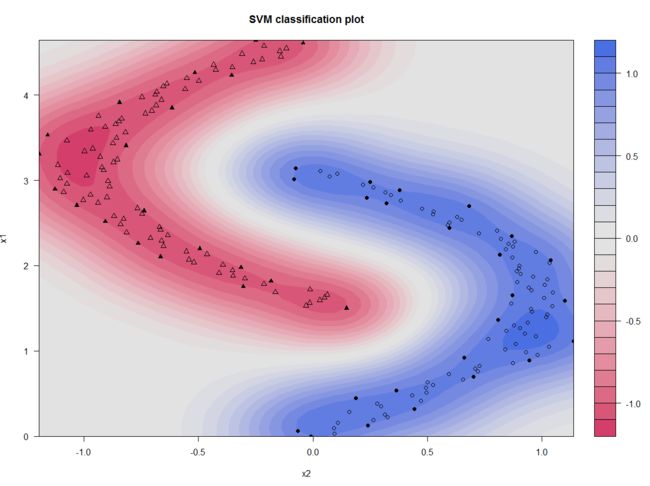
用图形来观察建模结果,下图是根据线性SVM得到个样本的判别值等高线图(判别值decision value相当于Logistic回归中的X,X取0时为决策边界)。可以清楚地看到决策边界为线性,中间的决策边缘显示为白色区域,有相当多的样本落入此区域。
plot(model1, data = LMdata$SVM)
下面为了更好的拟合,我们加大了C的取值,如下图。可以预料到,当加大C参数后决策边缘缩窄,也使误差减小,但仍有个别样本未被正确的分类。
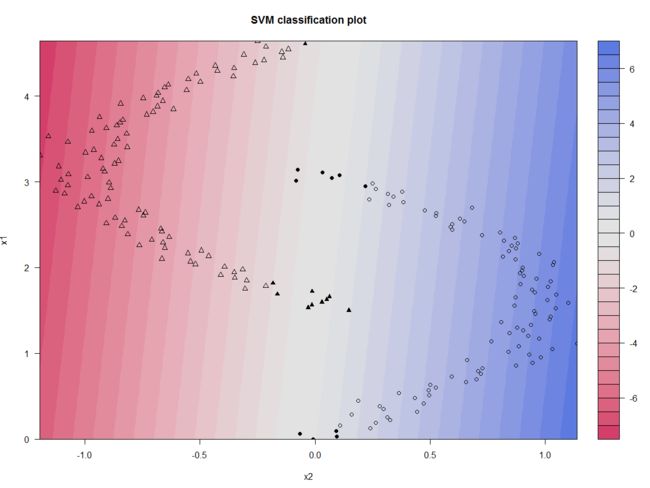
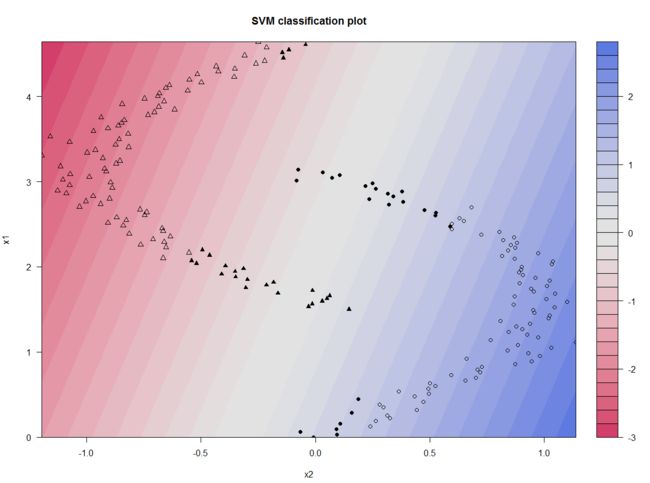
然后我们换用高斯核函数,这样得到了非线性决策边界。所有样本都得到了正确的分类。如下图
model3 <- ksvm(y~., data = LMdata$SVM, kernel = 'rbfdot', C = 1)
plot(model3, data = LMdata$SVM)
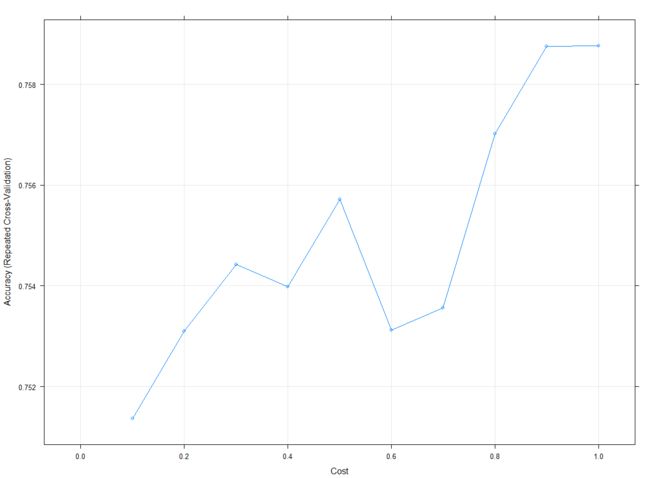
在实际的应用中,为了寻找最优参数我们用caret包来配合建模,如同前文介绍的那样,我们仍然使用多重交叉检验来评价模型,最终通过图形来展示参数和准确率之间的关系:
fitcontrol <- trainControl(method = 'repeatedcv',
number = 10, repeats = 3)
tunedf <- data.frame(.C=seq(0,1,length = 11))
svmmodel <- train(class~., data = procdata,
method = 'svmRadialCost', trControl = fitcontrol,
tuneGrid = tunedf)
plot(svmmodel)
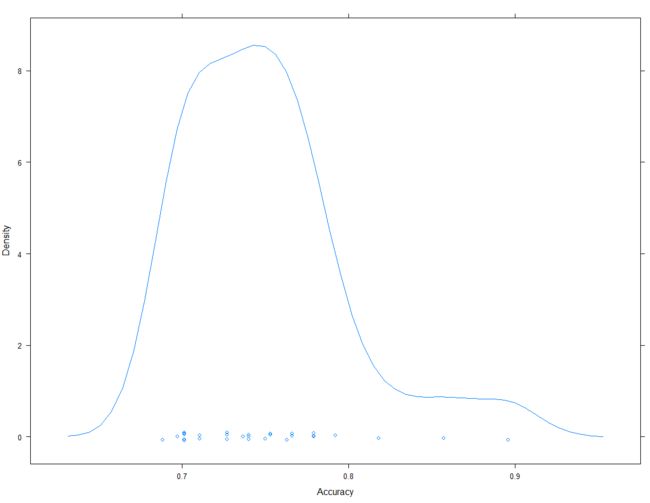
由上图可见,在C参数取值为0.4?时,模型得到最佳准确率。
SVM的特点在于他可以发现全局最优解,这不同于决策树或神经网络模型。他可以用参数来控制过度拟合问题,并通过选择核函数来处理不同的问题。当数据变量较多时,可以先尝试用线性核,例如在生物信息和文本挖掘方面。当变量较少时,可以考虑优先使用高斯核。
集成学习与随机森林
之前谈到的都是使用单个模型的训练和预测,能否将单个模型组合起来构成更为强大的预测系统呢?这正是近年来出现的集成学习(ensemble learning) 的思路。集成学习是试图通过连续调用单个学习算法,获得不同的模型,然后根据规则组合这些模型来解决同一个问题,可以显著地提高学习系统的泛化能力。
组合多个模型预测结果主要采用加权平均或投票的方法。在这里我们介绍最常用的集成学习算法 - 随机森林。
随机森林(Random Forest)是传统决策树方法的扩展,将多个决策树进行组合来提高预测精度。随机森林利用分类回归树作为其基本组成单元,也可称之为基学习器或是子模型。
随机森林计算步骤是,从原始训练样本中随机又放回地抽出N个样本;从解释变量中随机抽出M个变量;依据上述得到的子集实施CART方法(无需剪枝),从而形成一个单独的决策树;重复上面步骤X次,就构建了有X棵树的随机森林模型。在对新数据进行预测分类时,由X棵树分别预测,以投票方式综合最终结果。
R语言中的randomForest包可以实施随机森林算法,其重要参数有两个,一个是mtry,表示在抽取变量时的抽取数目M。另一个是迭代次数,即森林中决策树的数目ntree,一般缺省的mtry是全部变量数的开方数,ntree是500.从下面的结果看到参数mtry的最佳值是6。
library(caret)
library(randomForest)
fitcontrol <- trainControl(method = 'repeatedcv',
number = 10, repeats = 3)
rfmodel <- train(class~., data = procdata,
method = 'rf', trControl = fitcontrol,
tuneLength = 5)
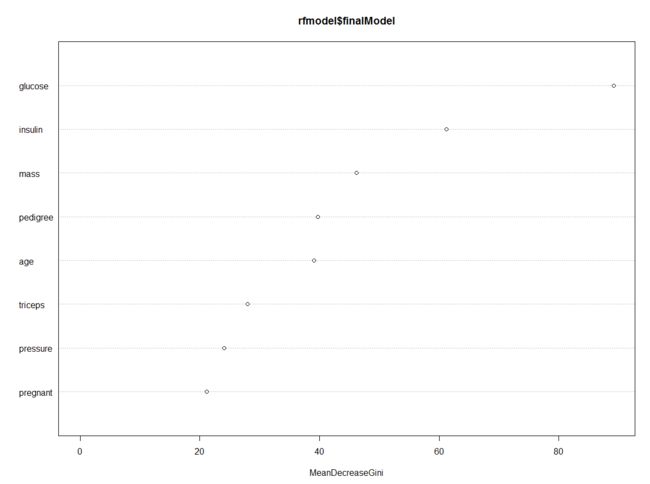
除了能用于回归分类之外,它还可以提供一些其他很有价值的功能。例如判断变量的重要程度。由于决策树是根据不同变量来分割数据,所以一棵树中能进行正确划分的变量就是最重要的变量。随机森林可以根据置换划分变量对分类误差的影响,来判断哪些变量是比较重要的。
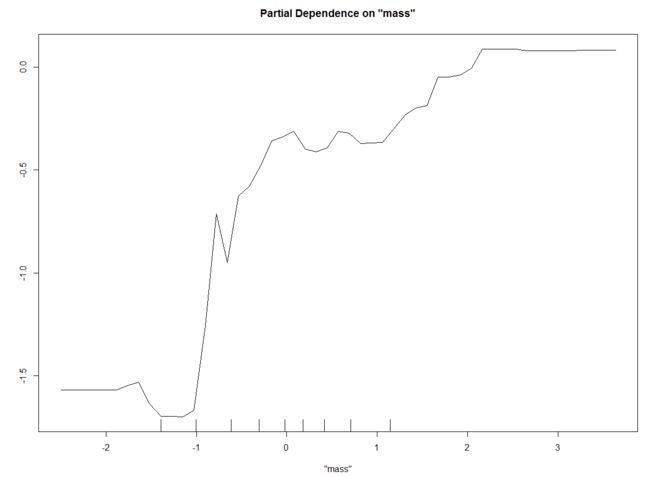
这个功能非常实用,特别在处理变量极多的数据集时,可以用它来作为变量选择的过滤器,然后再使用其他分类方法。randomForest包中的importance函数能返回各变量的重要程度,varImpplot函数可以用图形方式加以展现。partialPlot函数则能呈现变量的偏效应。rfcv函数用来得到最优的变量数目。
varImpPlot(rfmodel$finalModel)
partialPlot(rfmodel$finalModel, procdata[, -9],
'mass', which.class = 'pos')
从上两图可以观察到,glucose是影响糖尿病发生最重要的变量,而随着体重mass增加,患病风险也在增加。
随机森林的特点是准确率高、不会形成过拟合;速度快,能够处理大量数据,方便并行化处理;能处理很高维度的数据,不用做特征选择。