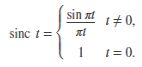Matlab通信仿真——带限系统下的基带信号

Matlab通信仿真——带限系统下的基带信号

Matlab通信仿真——带限系统下的基带信号

1 余弦滚降特性
满足消除码间串扰条件的H（f）有很多种，容易想到的一种极限情况，就是H（f）为理想低通型。
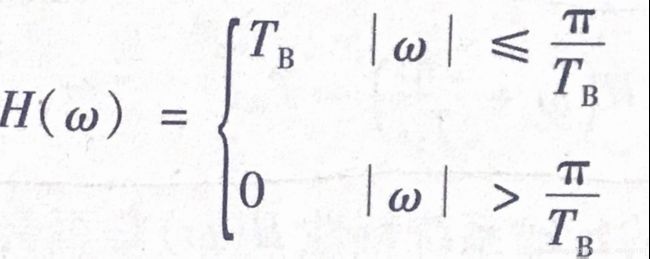图1.1 理想低通滤波器公式

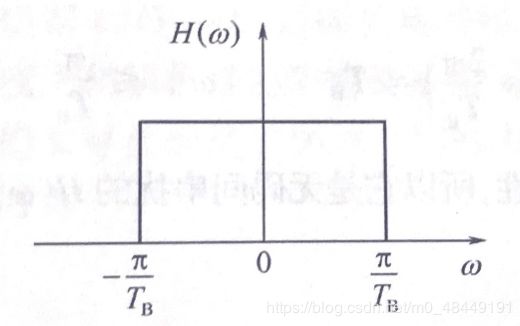
图1.2 理想低通型滤波器传输特性

令人遗憾的是，这种滤波器特性在物理上是无法实现的。
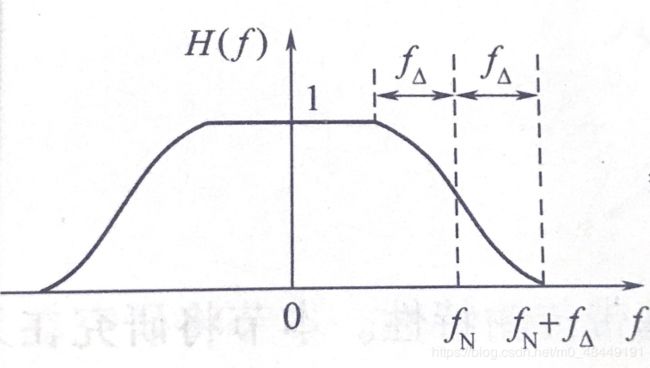
为了解决理想低通特性存在的问题，可以使理想低通低通滤波器特性的边缘缓慢下降，这称为“滚降”。一种常用的滚降特性是余弦滚降特性，如图1.3所示。一类常用的升余弦特性滚降的传输函数H（f）可表示为

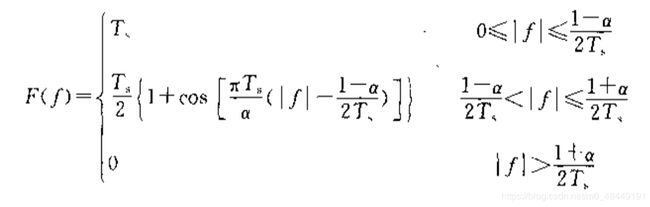（公式1.1）

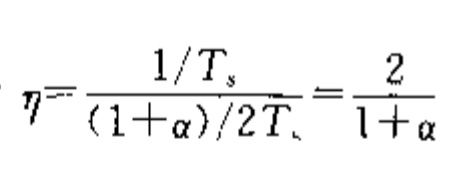
其中α称为滚降系数，频带利用率为（公式1.2）

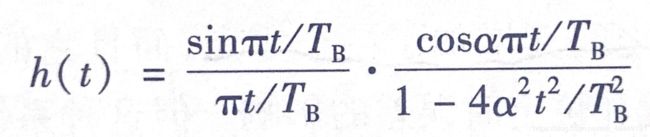
升余弦特性滚降系统的时域波形为（公式1.3）

图1.3 余弦滚降特性

1.1 设计不同α的升余弦滚降系统频谱
首先，完成初始化设置。设置码元周期，抽样、采样间隔，并把三个不同的滚降系数α（α分别等于0、0.5、1）赋给alpha。
对应代码如下：

// 
Ts=1;%码元周期
N_sample=17;%每个码元抽样点数
dt=Ts/N_sample;%抽样间隔
df=1.0/(20.0*Ts); 
t=-10*Ts:dt:10*Ts;%设置采样
f=-2/Ts:df:2/Ts;
alpha=[0,0.5,1];;

通过公式1.1，设计升余弦特性滚降系统的传输函数H（f）。利用for循环结构完成分段函数的设计，共有两次循环，第一层循环为α的循环，三个α对应三行，轮流把三个α代入式中进行运算，结果存入Xf矩阵中的三行中，第二层循环为k的循环，对应了每个f的抽样值，轮流代入式中进行运算，结果存入Xf矩阵中的每一列。
最终Xf（n，k）的结果共有三行，分别对应三个α值的结果，如图1.1.1。

图1.1.1 Xf输出结果
对应代码如下：

// for n=1:length(alpha)%三个滚降系数轮流显示
    for k=1:length(f)
        if abs(f(k))>0.5*(1+alpha(n))/Ts
            Xf(n,k)=0;
        elseif abs(f(k))<0.5*(1-alpha(n))/Ts
            Xf(n,k)=Ts;
        else
Xf(n,k)=0.5*Ts*(1+cos(pi*Ts/(alpha(n)+eps)*(abs(f(k))-0.5*(1-alpha(n))/Ts)));
        end
    end
Xt(n,:)=sinc(t/Ts).*(cos(alpha(n)*pi*t/Ts))./(1-4*alpha(n)^2*t.^2/Ts^2+eps);%赋值给Xt的第n行
End;

注：1.形如A(i, :)=b表示把b存入矩阵A的第i行

1.2 设计不同α的升余弦滚降系统时域波形
通过公式1.3，设计升余弦特性滚降系统的时域波形Xt。同样通过for循环完成三个不同α值得运算。共一层循环，第一层循环为α的循环，结果存入Xt矩阵中的三行，输出结果如下图1.2.1。

图1.2.1 Xt输出结果
对应代码如下：

// alpha=[0,0.5,1];%三个滚降系数
for n=1:length(alpha)%三个滚降系数轮流显示
Xt(n,:)=sinc(t/Ts).*(cos(alpha(n)*pi*t/Ts))./(1-4*alpha(n)^2*t.^2/Ts^2+eps);%赋值给Xt的第n行
End;

注：1.

2.形如A+eps，表示离A最近的浮点数

2 眼图
在实际生活中，我们使用简便的实验手段来定性评价系统的性能。
所谓眼图，是指通过示波器观察接收端的基带信号波形，从而估计和调整系统性能的一种方法。这种方法的具体做法是：用一个示波器跨接在抽样判决器的输入端，然后调整示波器水平扫描周期，使其与接收码元的周期同步。
此时可以从示波器显示的波形上，观察码间干扰和信道噪声等因素影响的情况，从而估计系统性能的优劣程度。因为在传输二进制信号波形时，示波器显示的波形很像人的眼睛，故名“眼图”，如图2.1。

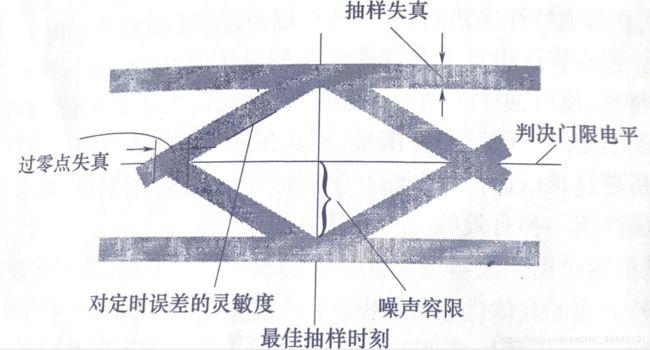
图2.1 眼图的模型
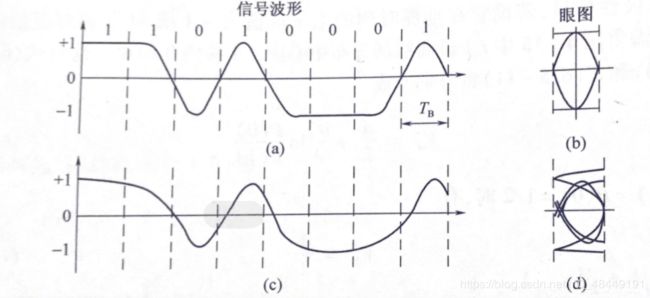
通俗易懂的说，眼图就是将每一个扫描周期调整到码元周期，由于示波器的余辉作用，扫描得到的每一个码元波形将重叠在一起，如果说没有码间干扰，如图2.2（b）所示的线条会是细而清晰的大“眼睛”。对比图2.2（b）和（d）可知，眼图的“眼睛”张开越大，且眼图越端正，表示码间串扰越小；反之，表示码间干扰越大。

图2.2 基带信号波形及眼图

图2.3 眼图设计流程图

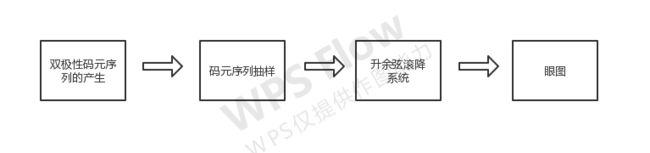
2.1 双极性码元序列的产生
产生双极性码元序列的操作步骤如下：
（1）完成程序的初始化设置，定义码元数、抽样点数等。
（2）调用randn函数，产生一个行数为1，列数为码元数N_data的正态分布随机 矩阵。
（3）调用sign函数，判断步骤（2）中产生的随机矩阵的每个元素的正负号，赋 给d。
（4）定义并调用sigexpand函数，对d进行扩张，每个间隔间加入N_sample个零， 赋值给xt，xt即为双极性码元序列，结果如图2.1.1。
图2.1.1 xt输出结果
操作代码如下：

// Ts=1;%码元周期
N_sample=17;%每个码元抽样点数
N_data=1000;%码元数

%产生双极性数字信号
d=sign(randn(1,N_data));%randn随机生成数字 sign函数进行一个判断，判断其正负
xt=sigexpand(d,N_sample);%对d进行扩张，每个间隔加入N_sample-1个零
%定义sigexpand函数
function[out]=sigexpand(d,M);
N=length(d);%基带信号码元长度
out=zeros(M,N);%矩阵M为采样点  N为基带信号码元数量,建立M*N的零矩阵
out(1,:)=d;%将零矩阵第一行换成基带信号中的8个码元
out=reshape(out,1,M*N);% 1行 m*n 列

%B = reshape(A,m,n) 返回一个m*n的矩阵B， B中元素是按列从A中得到的。如	 果A中元素个数没有m*n个， 则会引发错误。;

2.2码元序列抽样
设置抽样时间间隔dt=Ts/N_sample，设置采样，从-3Ts开始，到3Ts结束，步长为dt，t=-3Ts:dt:3Ts;
操作代码如下：

// 
dt=Ts/N_sample;%抽样时间间隔
t=-3*Ts:dt:3*Ts;%设置采样;

2.3 设置升余弦滚降系统
参考公式1.3,写出升余弦滚降特性系统函数的表达式，输出信号等于输入信号与系统函数的卷积。
操作代码如下：

// alpha=1;%滚降系数为1
%基带系统冲击响应（升余弦）
ht=sinc(t/Ts).*(cos(alpha*pi*t/Ts))./(1-4*alpha^2*t.^2/Ts^2+eps);
st=conv(xt,ht);%卷积，输出函数等于输入函数与系统函数的卷积
tt=-3*Ts:dt:(N_data+3)*N_sample*dt-dt;%设置采样;

注：
（1）带.和./指矩阵中各个元素对应相乘或相除
（2）sinc（t）=sin（pait）/（pai*t）
（3）形如A+eps，表示离A最近的浮点数

2.4绘制眼图
绘制眼图的步骤如下：
（1）定义眼图长度，显示8个“眼睛”。
（2）建立一个一行eye_num*N_sample列的零矩阵，定义采样间隔
（3）通过循环k画眼图，将48个周期重叠在一起，利用drawnow和holdon函数 形成眼图
操作代码如下：

// eye_num=8;
N_sample=17;%每个码元抽样点数
subplot(2,2,2); 
ss=zeros(1,eye_num*N_sample);%建立零矩阵
ttt=0:dt:eye_num*N_sample*dt-dt;%采样间隔
for k=3:50
    ss=st(k*N_sample+1:(k+eye_num)*N_sample);%st为输出函数
    drawnow;%将还未处理完的图像实时的显示出来，实时看到图像的每一步变化情况
    plot(ttt,ss);
    hold on;%新画图像之后不想覆盖原图像
end
xlabel('t/Ts');
ylabel('基带信号眼图');

注：（1）ss=st（a：b）表示将st矩阵中[st（a），st（a+1）…st（b）]这些元素 存入ss中

四、结果分析

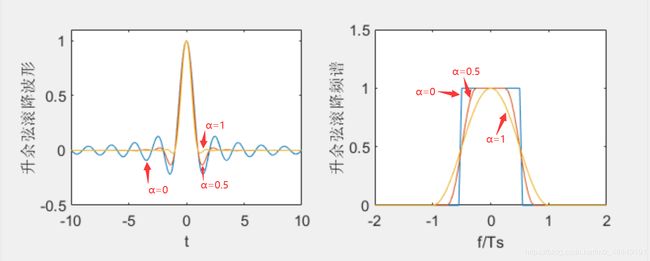
图4.1 的升余弦滚降系统频谱及其各自对应的时域波形图
由图4.1可知，在频谱中，α为0时，滤波器特性的边缘垂直，α越大，边缘倾斜程度越大。在时域中，α为0时，旁瓣最大，α越大，旁瓣越小。

图4.2 接收端的基带数字信号波形图及其眼图

所有的代码如下：
代码1
不同滚降系数的升余弦滚降系统频谱及其各自对应的时域波形：

// Ts=1;
N_sample=17;%每个码元抽样点数
dt=Ts/N_sample;%抽样间隔
df=1.0/(20.0*Ts);
 
t=-10*Ts:dt:10*Ts;%设置采样
f=-2/Ts:df:2/Ts;%
 
alpha=[0,0.5,1];%三个滚降系数
for n=1:length(alpha)%三个滚降系数轮流显示
    for k=1:length(f)
        if abs(f(k))>0.5*(1+alpha(n))/Ts
            Xf(n,k)=0;
        elseif abs(f(k))<0.5*(1-alpha(n))/Ts
            Xf(n,k)=Ts;
        else
Xf(n,k)=0.5*Ts*(1+cos(pi*Ts/(alpha(n)+eps)*(abs(f(k))-0.5*(1-alpha(n))/Ts)));
        end
    end
Xt(n,:)=sinc(t/Ts).*(cos(alpha(n)*pi*t/Ts))./(1-4*alpha(n)^2*t.^2/Ts^2+eps);%赋值给Xt的第n行
end
 
figure(1)
subplot(2,2,1)
plot(t,Xt);
axis([-10 10 -0.5 1.1]);
xlabel('t');
ylabel('升余弦滚降波形');
 
subplot(2,2,2)
plot(f,Xf);
axis([-2 2 0 1.5]);
xlabel('f/Ts');
ylabel('升余弦滚降波形');

代码二
若基带传输系统响应是的升余弦滚降系统，画出在接收端的基带数字信号波形及其眼图：

// clear all;
close all;
 
Ts=1;%码元周期
N_sample=17;%每个码元抽样点数
eye_num=8;
alpha=1;%滚降系数为1
N_data=1000;%码元数
 
dt=Ts/N_sample;%抽样时间间隔
t=-3*Ts:dt:3*Ts;%设置采样
 
%产生双极性数字信号
d=sign(randn(1,N_data));%randn随机生成数字 sign函数进行一个判断，判断其正负
xt=sigexpand(d,N_sample);%对d进行扩张，每个间隔加入N_sample-1个零
 
%基带系统冲击响应（升余弦）
ht=sinc(t/Ts).*(cos(alpha*pi*t/Ts))./(1-4*alpha^2*t.^2/Ts^2+eps);%公式P149，带.*和./指各个元素对应相乘或相除，sinc（t）=sin（pai*t）/pai*t
st=conv(xt,ht);%卷积函数
tt=-3*Ts:dt:(N_data+3)*N_sample*dt-dt;%设置采样
 
%基带数字信号波形
figure(1)
subplot(2,2,1);
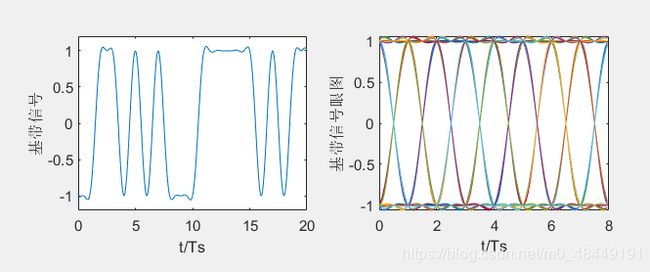
plot(tt,st);
axis([0 20 -1.2 1.2]);%横坐标范围，纵坐标范围
xlabel('t/Ts');
ylabel('基带信号');
%画眼图
subplot(2,2,2); 
ss=zeros(1,eye_num*N_sample);%建立零矩阵
ttt=0:dt:eye_num*N_sample*dt-dt;%采样间隔
for k=3:50
    ss=st(k*N_sample+1:(k+eye_num)*N_sample);
    drawnow;%将还未处理完的图像实时的显示出来，实时看到图像的每一步变化情况
    plot(ttt,ss);
    hold on;%新画图像之后不想覆盖原图像
end
xlabel('t/Ts');
ylabel('基带信号眼图')
定义函数代码如下：
function[out]=sigexpand(d,M);
N=length(d);%基带信号码元长度
out=zeros(M,N);%矩阵M为采样点  N为基带信号码元数量,建立M*N的零矩阵
out(1,:)=d;%将零矩阵第一行换成基带信号中的8个码元
out=reshape(out,1,M*N);% 1行 m*n 列
%B = reshape(A,m,n) 返回一个m*n的矩阵B， B中元素是按列从A中得到的。如果A中元素个数没有m*n个， 则会引发错误。;