数据结构与算法Python版之北大慕课笔记（一）

一、“变位词”判断问题

问题描述：变位词是指两个词之间存在组成字母的重新排列关系。如heart和earth，python和typhon。为了简单起见，假设参与判断的两个词仅由小写字母构成，且长度相等。

解题目标：写一个bool函数，以两个词作为参数，返回这两个词是否为变位词。

1. 解法一：逐字检查

解法思路：将词1中的字符逐个到词2检查是否存在，存在就打勾标记（防止重复检查），如果每个字符都能找到，则两个词是变位词，只要有一个字符找不到，就不是变位词。

程序技巧：实现打勾标记：将词2对应字符设为None，由于字符串是不可变类型，需要先复制到列表中。

代码实现：

# 解法一：逐字检查
def anangramSolution1(s1,s2):
    alist = list(s2)
    pos1 = 0
    stillOK = True
    while pos1 < len(s1) and stillOK:
        pos2 = 0
        found = False
        while pos2 < len(alist) and not found:
            if s1[pos1] == alist[pos2]:
                found = True
            else:
                pos2 = pos2 + 1
        if found:
            alist[pos2] = None
        else:
            stillOK = False
        pos1 = pos1 + 1
    return stillOK

print(anangramSolution1('heart','earth'))

代码时间复杂度：总执行次数为：1+2+3+…+n ，故时间复杂度为：O(n²)

2. 解法二：排序比较

解法思路：将两个字符串都按照字母顺序排好序，再逐个字符对比是否相同，如果相同则是变位词，有任何不同则不是变位词。

代码实现：

# 解法二：排序比较
def anagramSolution2(s1,s2):
    alist1 = list(s1)
    alist2 = list(s2)

    alist1.sort()
    alist2.sort()
    pos = 0
    matches = True
    while pos < len(s1) and matches:
        if alist1[pos] == alist2[pos]:
            pos = pos + 1
        else:
            matches = False
    return matches

print(anagramSolution2('heart','earth'))

代码时间复杂度：本算法时间主导的步骤是排序步骤，所以时间复杂度就等于排序的时间复杂度：O(nlogn)

3. 解法三：计数比较

解法思路：对比两个词中每个字母出现的次数，如果26个字母出现次数都相同的话，这两个字符串就一定是变位词。

具体做法：为每个词设置一个26位计数器，先检查每个词，在计数器中设定好每个字母出现的次数。计数完成后，进入比较阶段，看两个字符串的计数器是否相同，如果相同则说明是变位词。

代码实现：

# 解法三：计数比较
def anagramSolution3(s1,s2):
    c1 = [0] * 26
    c2 = [0] * 26
    for i in range(len(s1)):
        pos = ord(s1[i]) - ord('a') # ord()返回一个字母的unicode编码
        c1[pos] = c1[pos] + 1
    for i in range(len(s2)):
        pos = ord(s2[i]) - ord('a')
        c2[pos] = c2[pos] + 1
    j = 0
    stillOK = True
    while j < 26 and stillOK:
        if c1[j] == c2[j]:
            j = j + 1
        else:
            stillOK = False
    return stillOK

print(anagramSolution3('heart','earth'))

代码时间复杂度：前两个循环用于对字符串进行计数，操作次数等于字符串长度n，第三个循环用于计数器比较，操作次数为26。所以该代码总操作次数为：2n+26，时间复杂度为：O(n)

注：该代码也采用了 “用空间换时间” 的思想。

二、线性结构linear structure

线性结构是一种有序数据项的集合，其中每个数据项都有唯一的前驱和后继。

• 除了第一个没有前驱，最后一个没有后继。
• 新的数据项加入到数据集中时，只会加入到原有某个数据项之前或之后。
• 具有这种性质的数据集，就称为线性结构。

1. 四个线性结构

• 栈 stack —— 后进先出（LIFO：last in first out）
• 队列 queue —— 先进先出（FIFO：first in first out）
• 双端队列 deque
• 列表 list

2. 栈的应用

2.1 括号匹配

from pythonds.basic.stack import Stack

def parChecker(symbolString):
    s = Stack()
    balanced = True
    index = 0
    while index < len(symbolString) and balanced:
        symbol = symbolString[index]
        if symbol == "(":
            s.push(symbol)
        else:
            if s.isEmpty():
                balanced = False
            else:
                s.pop()
        index = index + 1

    if balanced and s.isEmpty():
        return True
    else:
        return False

print(parChecker('((()))'))
print(parChecker('(()'))

2.2 进制转换

from pythonds.basic.stack import Stack

def baseConverter(decNumber,base):
    digits = "0123456789ABCDEF"
    remstack = Stack()

    while decNumber > 0:
        rem = decNumber % base
        remstack.push(rem)
        decNumber = decNumber // base

    newString = ""
    while not remstack.isEmpty():
        newString = newString + digits[remstack.pop()]

    return newString

print(baseConverter(25,2))
print(baseConverter(25,16))

2.3 表达式转换及求值

2.3.1 中缀表达式

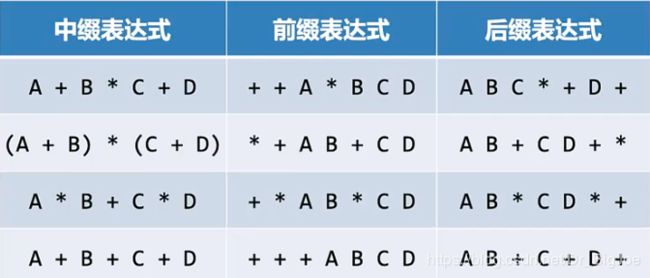
• 中缀表达式形式：第一操作数、操作符、第二操作数。
• 中缀(infix)表达式：A + B * C + D ，为了避免计算顺序混淆，引入全括号表达式；
• 全括号中缀表达式：((A + (B * C)) + D)

2.3.2 前缀和后缀表达式

• 前缀(prefix)表达式：将操作符移到前面，形式变为：操作符、第一操作数、第二操作数。
• 后缀(postfix)表达式：将操作符移到后面，形式变为：第一操作数、第二操作数、操作符。

2.4 中缀转换为前缀/后缀表达式

例：(A + (B * C))

• 把操作符移到子表达式(B * C)的右括号位置替代它，再删去左括号得到BC，接着把操作符+移到相应的右括号并删掉左括号，表达式就转为 后缀 形式，即：ABC*+ 。
• 同理，把操作符移到相应的左括号替代之，并删掉右括号，表达时就转换为 前缀 形式，即：+A*BC 。
• 总结：无论表达式多复杂，转换为前缀或后缀只需要两个步骤：
  (1) 将中缀表达式转换为全括号形式；
  (2) 将所有操作符移动到子表达式所在的左括号（前缀）或者右括号（后缀）处，替代之，再删除所有括号。

2.4.1 通用的中缀转后缀算法

流程：

• 从左到右扫描中缀表达式单词列表，如果单词是操作数，则直接添加到后缀表达式列表的末尾；如果单词是左括号，则压入opstack栈顶；如果单词是右括号，则反复弹出opstack栈顶操作符，加入到输出列表末尾，直到碰到左括号；如果单词是操作符，则压入opstack栈顶，但在压入栈顶之前，要比较其与栈顶操作符的优先级，如果栈顶的高于或等于它，就要反复弹出栈顶操作符，加入到输出列表末尾；直到栈顶的操作符优先级低于它。
• 中缀表达式单词列表扫描结束后，把opstack栈中的所有剩余操作符
  依次弹出，添加到输出列表末尾。
• 把输出列表再用join方法合并成后缀表达式字符串，算法结束。

代码实现：

from pythonds.basic.stack import Stack

def infixToPostfix(infixexpr):
    prec = {}
    prec["*"] = 3
    prec["/"] = 3
    prec["+"] = 2
    prec["-"] = 2
    prec["("] = 1
    opStack = Stack()
    postfixList = []
    tokenList = infixexpr.split()

    for token in tokenList:
        if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
            postfixList.append(token)
        elif token == '(':
            opStack.push(token)
        elif token == ')':
            topToken = opStack.pop()
            while topToken != '(':
                postfixList.append(topToken)
                topToken = opStack.pop()
        else:
            while (not opStack.isEmpty()) and \
                (prec[opStack.peek()] >= prec[token]):
                postfixList.append(opStack.pop())
            opStack.push(token)
    while not opStack.isEmpty():
        postfixList.append(opStack.pop())
    return " ".join(postfixList)

2.5 后缀表达式求值

流程：

• 创建空栈operandStack用于暂存操作数。
• 将后缀表达式用split方法解析为单词（token）的列表。
• 从左到右扫描单词列表，如果单词是一个操作数，将单词转换为整数int，压入operandStack栈顶；如果单词是一个操作符，就开始求值，从栈顶弹出两个操作数，先弹出的是右操作数，后弹出的是左操作数，计算后将值重新压入栈顶。
• 单词列表扫描结束后，表达式的值就在栈顶。
• 弹出栈顶的值，返回。

代码实现：

from pythonds.basic.stack import Stack

def postfixEval(postfixExpr):
    operandStack = Stack()
    tokenList = postfixExpr.split()

    for token in tokenList:
        if token in "0123456789":
            operandStack.push(int(token))
        else:
            operand2 = operandStack.pop()
            operand1 = operandStack.pop()
            result = doMath(token,operand1,operand2)
            operandStack.push(result)
    return operandStack.pop()

def doMath(op,op1,op2):
    if op == "*":
        return op1 * op2
    elif op == "/":
        return op1 / op2
    elif op == "+":
        return op1 + op2
    else:
        return op1 - op2

3. 队列的应用

3.1 热土豆（约瑟夫问题）

流程：

• 用队列来实现热土豆问题的算法，参加游戏的人名列表，以及传土豆次数num，算法返回最后剩下的人名。
• 采用队列存放参加游戏的人名，按照传递土豆方向从队首排到队尾，游戏时，队首始终是持有土豆的人。
• 游戏开始，只需要将队首的人出队，随即再到队尾入队，算是土豆的一次传递，传递了num次后，将队首的人移除，不再入队，如此反复，直到队里剩余1个人。

代码实现：

from pythonds.basic.queue import Queue

def hotPotato(namelist,num):
    simqueue = Queue()
    for name in namelist:
        simqueue.enqueue(name)

    while simqueue.size() > 1:
        for i in range(num):
            simqueue.enqueue(simqueue.dequeue())
        simqueue.dequeue()

    return simqueue.dequeue()
# 从1数到5，第五个人出列
print(hotPotato(["A","B","C","D","E","F","G"],4))

3.2 打印任务

打印任务具体实例配置如下：一个实验室，在任意的一个小时内，大约有10名学生在场，这一小时中，每人会发起两次打印任务，每次1-20页。
打印机的性能是：以草稿模式打印的话，每分钟10页；以正常模式打印的话，打印质量好，但速度下降为每分钟5页。
决策支持：找到一个让大家都不会等太久，又能尽量提高打印质量。

问题建模：

• 对象：打印任务、打印队列、打印机
  打印任务的属性：提交时间，打印页数
  打印队列的属性：具有FIFO性质的打印任务队列
  打印机的属性：打印速度，是否在忙
• 过程：生成和提交打印任务：
  确定生成概率：每180秒会有一个作业生成并提交，概率为每秒1/180
  确定打印页数：实例是1-20页，也就是1-20页之间概率相同
• 过程：实施打印：
  当前打印就是正在打印的作业
  新作业开始打印时开始倒计时，回0表示打印完毕，可以处理下一个作业
• 模拟时间：
  统一的时间框架：以秒均匀流逝的时间，设定结束时间
  同步所有过程：在一个时间单位里，对生成打印任务和实施打印两个过程各处理一次

模拟流程：

• 创建打印队列对象。
• 时间按照秒的单位流逝。按照概率生成打印作业，加入打印队列；如果打印机空闲且队列不空，则取出队首作业打印，记录此作业等待时间；如果打印机忙，则按照打印速度进行1秒打印；如果当前作业打印完成，则打印机进入空闲。
• 时间用尽，开始统计平均等待时间。

代码实现：

from pythonds.basic.queue import Queue
import random

class Printer:
    def __init__(self,ppm):
        self.pagerate = ppm # 打印速度
        self.currentTask = None # 打印任务
        self.timeRemaining = 0  # 任务倒计时

    def tick(self):  # 打印1秒
        if self.currentTask != None:
            self.timeRemaining = self.timeRemaining - 1
            if self.timeRemaining <= 0:
                self.currentTask = None

    def busy(self):  # 打印是否忙
        if self.currentTask != None:
            return True
        else:
            return False

    def startNext(self,newtask):  # 打印新作业
        self.currentTask = newtask
        self.timeRemaining = newtask.getPages()*60/self.pagerate

class Task:
    def __init__(self,time):
        self.timestamp = time  # 生成时间戳
        self.pages = random.randrange(1,21)  # 打印页数

    def getStamp(self):
        return self.timestamp

    def getPages(self):
        return self.pages

    def waitTime(self,currenttime):
        return currenttime - self.timestamp  # 等待时间

def newPrintTask():
    num = random.randrange(1,181)  # 1/180概率生成作业
    if num == 180:
        return True
    else:
        return False

def simulation(numSeconds,pagesPerMinute):
    labprinter = Printer(pagesPerMinute)
    printQueue = Queue()
    waitingtimes = []

    for currentSecond in range(numSeconds):
        if newPrintTask():
            task = Task(currentSecond)
            printQueue.enqueue(task)

        if (not labprinter.busy()) and (not printQueue.isEmpty()):
            nexttask = printQueue.dequeue()
            waitingtimes.append(nexttask.waitTime(currentSecond))
            labprinter.startNext(nexttask)

        labprinter.tick()

    averageWait = sum(waitingtimes)/len(waitingtimes)
    print("Average Wait %6.2f secs %3d tasks remaining." \
                %(averageWait,printQueue.size()))

for i in range(10):
    simulation(3600,10)

4. 双端队列的应用

• 双端队列是一种有次序的数据集，数据项既可以从队首加入，也可以从队尾加入，数据项也可以从两端删除；某种意义上说，双端队列集成了栈和队列的能力。
• 但双端队列并不具有内在的LIFO和FIFO特性，如果用双端队列来模拟栈和队列，需要由使用者自行维护操作的一致性。

4.1 回文词判定

用双端队列很容易解决回文词问题，先将需要判定的词从队尾加入deque，再从两端同时移除字符判定是否相同，直到deque中剩下0个或1个字符。

实现代码：

from pythonds.basic.deque import Deque

def palchecker(aString):
    chardeque = Deque()

    for ch in aString:
        chardeque.addRear(ch)

    stillEqual = True
    while chardeque.size() > 1 and stillEqual:
        first = chardeque.removeFront()
        last = chardeque.removeRear()
        if first != last:
            stillEqual = False
    return stillEqual

print(palchecker("lsdkjfskf"))
print(palchecker("radar"))

4.2 采用链表实现无序表UnorderedList

• 虽然列表数据结构要求保持数据项的前后相对位置，但这种前后位置的保持，并不要求数据项依次存放在连续的存储空间。
• 如下图，数据项存放位置并没有规则，但如果在数据项之间建立链接指向，就可以保持其前后相对位置。第一个和最后一个数据项需要显示标记出来，一个是队首，一个是队尾，后面再无数据了。
  

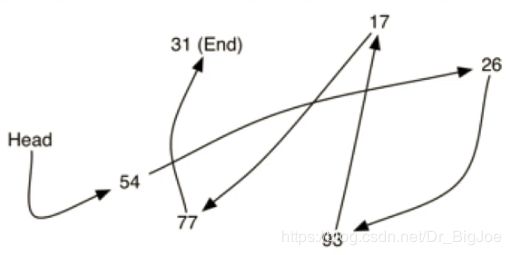
链表实现：节点Node

• 链表实现的最基本元素是节点Node，每个节点至少要包含两个信息：数据项本身、以及指向下一个节点的引用信息。注意next为None的意义是没有下一个节点了。

链表实现：无序表UnorderedList

• 可以采用链接节点的方式构建数据集来实现无序表。
• 链表的第一个和最后一个节点最重要。如果想访问到链表中的所有节点，就必须从一个节点开始沿着链接遍历下去。
• 所以无序表必须要有对第一个节点的引用信息，设立一个属性head，保存对第一个节点的引用，空表的head为None。
• 随着数据项的加入，无序表的head始终指向链条的第一个节点，无序表mylist对象本身并不包含数据项（数据项在节点中）。其中包含的head只是对首个节点Node的引用，判断空表的isEmpty()很容易实现。
• 无序表实现add方法，按照实现的性能考虑，应该添加到最容易加入的位置上，也就是表头，整个链表的首位置。
  

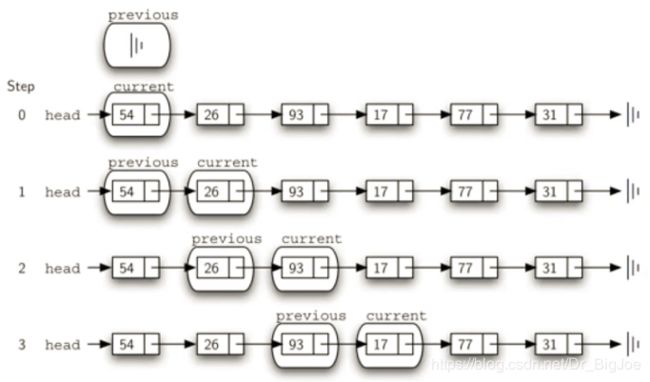
链表实现：size

• 从链表头head开始遍历到表尾同时用变量累加经过的节点个数。

链表实现：search

• 从链表头head开始遍历到表尾，同时判断当前节点的数据项是否为目标。

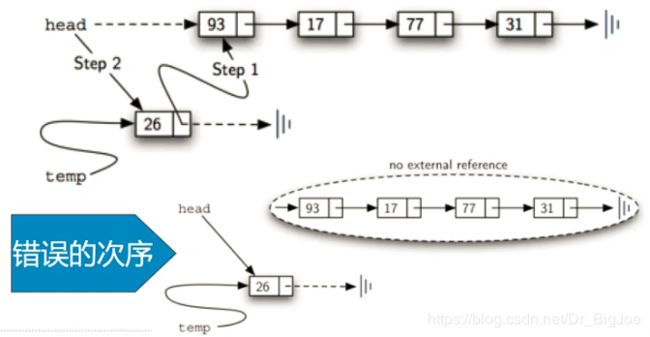
链表实现：remove(item)方法

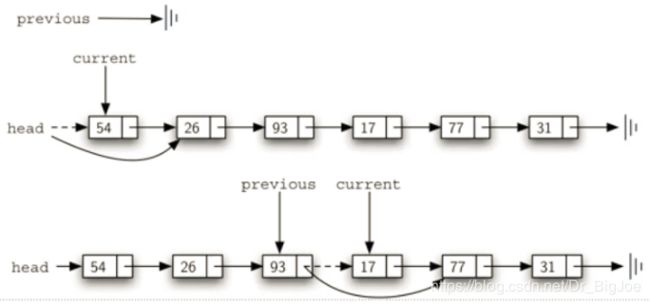
• 首先找到item，这个过程和search一样，但删除节点时，需要特别的技巧。
• current指向的是当前匹配数据项的节点，而删除需要把前一个节点的next指向current的下一个节点，所以我们在查找current的同时，还要维护前一个(previous)节点的引用。
  
• 找到item后，current指向item节点，previous指向前一个节点，开始执行删除，需要区分两种情况：current是首个节点；或者是位于链条中间的节点。
  

代码实现：

class Node:
    def __init__(self,initdata):
        self.data = initdata
        self.next = None

    def getData(self):
        return self.data

    def getNext(self):
        return self.next

    def setData(self,newdata):
        self.data = newdata

    def setNext(self,newnext):
        self.next = newnext

class UnorderedList:
    def __init__(self):
        self.head = None

    def add(self,item):
        temp = Node(item)
        temp.setNext(self.head)
        self.head = temp

    def size(self):
        current = self.head
        count = 0
        while current != None:
            count = count + 1
            current = current.getNext()
        return count

    def search(self,item):
        current = self.head
        found = False
        while current != None and not found:
            if current.getData() == item:
                found = True
            else:
                current = current.getNext()
        return found

    def remove(self,item):
        current = self.head
        previous = None
        found = False
        while not found:
            if current.getData() == item:
                found = True
            else:
                previous = current
                current = current.getNext()
        if previous == None:
            self.head = current.getNext()
        else:
            previous.setNext(current.getNext())

4.3 采用链表实现有序表OrderedList

• 在实现有序表时，需要记住数据项的相对位置，取决于他们之间的“大小”比较，Node定义相同，OrderedList也设置一个head来保存链表表头的引用。
• 对于isEmpty()，size()，remove()方法与节点次序无关，其实现与UnorderedList相同。
• search和add方法需要修改。

有序表实现：search方法

• 在无序表的search中，如果需要查找的数据项不存在，则会搜遍整个链表，直到表尾。
• 对于有序表来说，可以利用链表节点有序排列的特性，来为search节省不存在数据项的查找时间。一旦当前节点的数据项大于所要查找的数据项，则说明链表后面已经不可能再有要查找的数据项，可以直接返回False。

有序表实现：add方法

• add方法必须保证加入的数据项添加在合适的位置，以维护整个链表的有序性。
• 从头找到第一个比添加项大的数据项，将添加项插到该数据项前面。
• 跟remove方法类似，引入一个previous，跟随当前节点current。

代码实现：

class Node:
    def __init__(self,initdata):
        self.data = initdata
        self.next = None

    def getData(self):
        return self.data

    def getNext(self):
        return self.next

    def setData(self,newdata):
        self.data = newdata

    def setNext(self,newnext):
        self.next = newnext

class OrderedList:
    def __init__(self):
        self.head = None

    def search(self,item):
        current = self.head
        found = False
        stop = False
        while current != None and not found and not stop:
            if current.getData() == item:
                found = True
            else:
                if current.getData() > item:
                    stop = True
                else:
                    current = current.getNext()
        return found

    def add(self,item):
        current = self.head
        previous = None
        stop = False
        while current != None and not stop:
            if current.getData() > item:
                stop = True
            else:
                previous = current
                current = current.getNext()
        temp = Node(item)
        if previous == None:
            temp.setNext(self.head)
            self.head = temp
        else:
            temp.setNext(current)
            previous.setNext(temp)

=================================================================
以上均为个人学习笔记总结，学习代码见week18
课程名称：数据结构与算法Python版_北京大学_中国大学MOOC(慕课)
课程主页: http://gis4g.pku.edu.cn/course/pythonds/