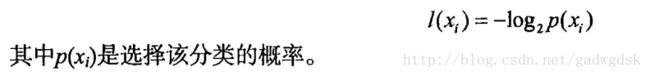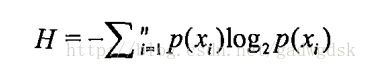决策树(ID3算法)
决策树学习笔记
1、决策树的概念
顾名思义,决策树是用来:根据已知的若干条件,来对事件作出判断。从根节点到叶子节点,是将不同特征不断划分的过程,最后将类别分出。
在理论学习前,先了解下面一个例子:
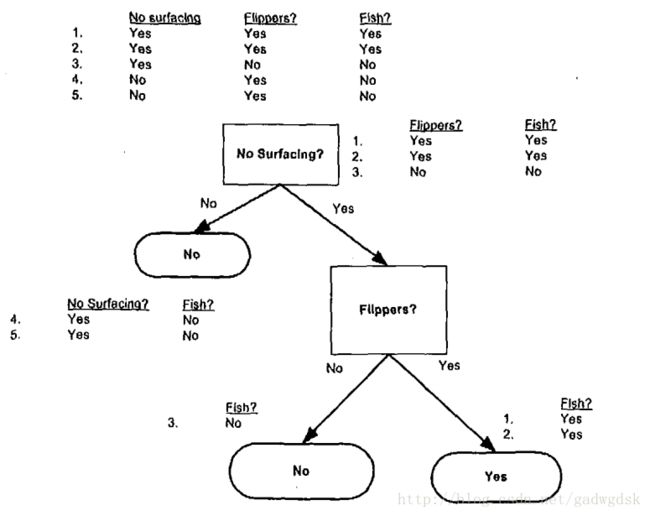
如下图所示,根据“不浮出水面是否可以生存”和“是否有脚蹼”两种特征来判断该海洋动物是否鱼类。图中有5个样本,样本中有两种是鱼类,三种不是鱼类。
可建立的特征向量如下:
_data_set = [[1, 1, "yes"],
[1, 1, "yes"],
[1, 0, "no"],
[0, 1, "no"],
[0, 1, "no"]]
_labels = ["no surfacing", "flippers"]2、用ID3算法来构造决策树
ID3算法将信息增益做贪心算法来划分算法,总是挑选是的信息增益最大的特征来划分数据,使得数据更加有序。
2.1信息增益
熵:熵是信息的期望,一般表示信息的混乱、无序程度
信息的定义如下:
于是信息的期望,熵的定义为:
信息增益指的是熵减小的量,也就是,数据集变得有序了多少。
下面给出熵的计算代码,直接输入上面给出的数据集可以得到信息熵
# 计算香农熵
def calc_shannon_ent(dataset):
n = len(dataset)
label_counts = {}
# 统计每个类别出现的次数
for feature in dataset:
label = feature[-1]
if label not in label_counts:
label_counts[label] = 0 # 创建该元素并清零
label_counts[label] += 1
entropy = 0
for key in label_counts:
p = float(label_counts[key]) / n # 计算类概率,或者说类在所有数据中的比例
entropy -= p * log(p, 2)
return entropy再次注意:特征向量最后一维是类别标签
2.2数据集划分
构造树的过程中,要将数据进行划分,为了方便,写一个子函数专门做数据划分,划分的原则是:挑出指定维度上和指定值相等的所有特征向量,并将该维去除后返回
# 在axis维度上对dataset进行划分,抽取axis维度上等于value的特征,这里没有用pandas,否则不需要这么麻烦
def splite_dataset(dataset, axis, value):
splt_dset = []
for f in dataset:
if f[axis] == value:
reduce_fv = f[:axis]
reduce_fv.extend(f[axis+1:])
splt_dset.append(reduce_fv)
return splt_dset遍历每一个特征,尝试使用每一个特征划分数据集,并计算对应的信息增益,选择最大的那一个特征来划分数据。值得注意的是,这里并不是使用二分类划分,而是,对应的特征有多少个值就将数据集划分为几个子集。在海洋动物的例子中,只是恰好两个特征都只有两个值。
# 通过遍历所有的特征,求取熵最小的划分方式
# 返回划分数据最好的特征,和最大的信息增益
def min_entropy_split_feature(dataset):
f_n = len(dataset[0]) - 1
base_entropy = calc_shannon_ent(dataset)
best_info_gain = 0.0
#print("entropy calc:"+str(dataset))
best_feature = -1
for i in range(f_n):
f_list = [feature[i] for feature in dataset]
unique_values = set(f_list)
new_entropy = 0.0
for value in unique_values:
sub_dataset = splite_dataset(dataset, i, value)
pro = len(sub_dataset) / float(len(dataset))
new_entropy += pro * calc_shannon_ent(sub_dataset)
info_gain = base_entropy - new_entropy # 信息增益是信息熵的减小量
if info_gain > best_info_gain:
best_info_gain = info_gain
best_feature = i
return best_feature, best_info_gain2.4递归构建决策树
2.3中给出了划分数据集的方法,可以使得数据局部整体上最有序,划分得到若干个子数据集中依然可以继续划分,使用同样的方法使得子数据集最有序,依次递归进行,直到最底层子数据集中只有一个类别
# 递归构建决策树
def create_tree(dataset, __labels):
labels = __labels.copy()
classlist = [f[-1] for f in dataset]
# 只剩下一个类了,因此返回类名称
if classlist.count(classlist[0]) == len(classlist):
return classlist[0]
# 数据集中只剩下最后一列了,也就是所有的特征都用完了,没法再向下分类了
# 这时候如果数据集中有多个类,那就认为是出现最多的那个类
# 实际中应该是,所给定的特征无法将数据进行完全分类导致的
if len(dataset[0]) == 1:
# print("******")
return majority_cnt(classlist)
bestfeature = min_entropy_split_feature(dataset)[0]
# if bestfeature >= len(labels):
# print("**************index out of range")
# print(dataset)
# print(labels)
# print(bestfeature)
bestf_label = labels[bestfeature]
newtree = {bestf_label: {}}
del labels[bestfeature]
f_values = [f[bestfeature] for f in dataset] # 找出bestfeature全部取值
unique_f_values = set(f_values)
for v in unique_f_values:
sublabels = labels[:]
_splitedtree = splite_dataset(dataset, bestfeature, v)
# print("xxxxxxxxxxxxxx seperate:")
# print("best fv:" + str(bestfeature) + " v:" + str(v))
# print(_splitedtree)
# print(labels)
newtree[bestf_label][v] = create_tree(_splitedtree.copy(), sublabels)
return newtree上面还用了一个子函数,是当数据集只剩下一列(最后一列,也就是类别),但是无法完全分类,就返回剩下的数据集中出现最多的那个类别
# 计算数据集中的主要类别,这里计算是鱼的多还是不是鱼的多,其实就是判断yes多还是no多
# 其他应用中可能会出现多个类别标签,因此这是一个通用函数
def majority_cnt(classlist):
classcount = {}
for label in classlist:
if label not in classcount.keys(): # 字典的键中不包含label
classcount[label] = 0
classcount[label] += 1
# classcount.items()是以list形式返回字典的键值:dict_items([('yes', 2), ('no', 4)])
# key中指定值获取函数,x[1]表示用键值对第二个参数来排序
# reverse表示降序排序,默认是ascending
sorted_class_count = sorted(classcount.items(), key=lambda x: x[1], reverse=True)
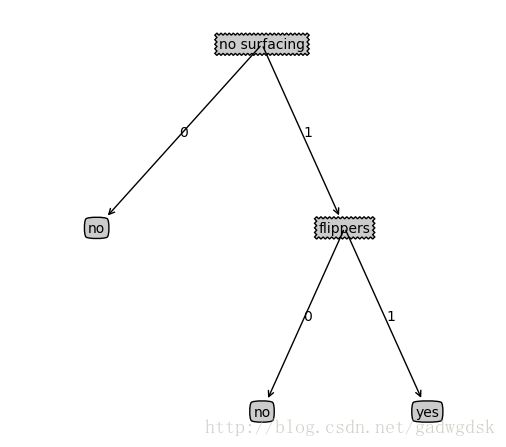
return sorted_class_count[0][0] # 返回出现次数最多的类的标签最后构建得到的决策树输入所示:
3、用决策树来做分类
上面构造了决策树,通过使用create_tree方法可以得到字典储存的决策树。输入一个新的特征向量,利用决策树,沿着树从上到下,可以得到分类。下面给出分类代码:
# 用构建好的决策树来进行分类
def classify(input_tree, feature_labels, test_fv):
classlabel = "none"
first_label = list(input_tree.keys())[0] # 获取输入字典中的第一个键
new_dict = input_tree[first_label] #
feature_index = feature_labels.index(first_label) # 获取first_label是第几个特征
for key in new_dict.keys():
if test_fv[feature_index] == key: # 注意,key是特征的值
if type(new_dict[key]).__name__ == "dict":
classlabel = classify(new_dict[key], feature_labels, test_fv)
else:
classlabel = new_dict[key]
return classlabel4总结
构建决策树可以用来做分类,其他用途尚不清楚。使用了贪心法,每次划分都是选择信息增益最大的,推测这样不一定能得到全局最大增益。除了ID3算法构造决策树,较为流行的还有C4.5和CART算法,后面继续学习。
决策树做分类似乎只能对简单特征分类,如果出现长度、宽度、距离等浮点数据时候无法分类,暂时不知道怎么处理。
参考文献:《机器学习实战》