第二章 Python基础介绍

第二章 Python基础介绍

2.0 命名规范

• Python 编码规范与命名规范
• Python3中的命名规范大全—基于PEP8标准

2.1 Python安装&基本界面

• Python
• Anaconda
• 集成开发环境 [Spyder]
• [jupyter-notebook] 网页版运行程序

统计相关Python模块

• NumPy: 数组与矩阵计算
• Pandas: 数据结构与数据分析
• Matplotlib: 图形绘制
• SciPy: 科学计算
• StatsModels: 统计模型
• Scikit-learn: 机器学习

2.2 Python内建数据结构、函数和文件

2.2.1 基本简单数据类型

菜鸟教程

• Number 数字
  • int 整数
  • float 浮点
  • complex 复数
• str 字符串
• bool 布尔
• range 序列

2.2.2 基本复合数据类型

• list 列表
• tuple 元组
• dict 字典
• set 集合

2.2.3 运算符&控制语句

• 运算符
• 条件控制
• 循环控制

2.2.4 进阶#1

• 迭代器和生成器
• 函数
• 模块
• 面向对象

2.2.5 进阶#2

• 数据结构
• 文件的读写
• OS
• 正则表达式
• 标椎库

2.3 Numpy

numpy = numerical python

• 线性代数
• 随机数生成
• 数组和矩阵
• 傅立叶分析

2.3.1 随机数生成

import numpy as np
import pandas as pd

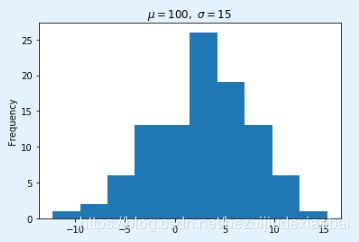
生成 100 个正态分布 N(3, 5) 的随机数

np.random.normal(3,5,100)

pd.Series(np.random.normal(3, 5, 100)).plot(kind='hist', title=r'$\mu=100,\ \sigma=15$')

生成 100 个 [0, 10] 之间均匀分布的整数随机数

np.random.randint(0,11,100)

pd.Series(np.random.randint(0, 11, 100)).unique()

pd.Series(np.random.randint(0, 11, 100)).value_counts()

pd.Series(np.random.randint(0, 11, 100)).value_counts().plot.bar()

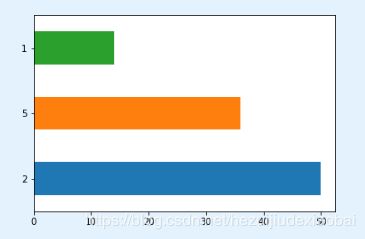
按下述分布列生成 100 个随机数

np.random.choice([1, 2, 5], 100, replace=True, p=[0.2,0.5,0.3])

pd.Series(np.random.choice([1, 2, 5], 100, replace=True, p=[0.2,0.5,0.3])).unique()

pd.Series(np.random.choice([1, 2, 5], 100, replace=True, p=[0.2,0.5,0.3])).value_counts()

pd.Series(np.random.choice([1, 2, 5], 100, replace=True, p=[0.2,0.5,0.3])).value_counts().plot.bar()

2.3.2 数组和矩阵

创建一个数组并求其差分得到的数组

x = np.array([1, 2, 3, 5, 9])
np.diff(x)

创建一个矩阵，并求其行列式的值

y = np.matrix('1, 2; 3,4')
np.linalg.det(y)

计算矩阵的特征值与特征向量

A = np.matrix('1, 3; 2, 5') # 定义变量 A 为一个矩阵
A

ev,P = np.linalg.eig(A) # 计算 A 的特征值与特征向量
ev

P

D = np.diag(ev) # 将两个特征值写成对角阵
D

np.dot(A,P) # 计算矩阵乘积 AP

np.dot(P,D) # 计算矩阵乘积 PA

2.4 Pandas

pandas = python data analysis
DataFrame
Pandas数据可视化

2.5 Matplotlib

Matplotlib数据可视化

2.6 Statsmodels

2.6.1 简介

实现各种统计模型和假设检验

2.6.2 使用数组实现普通最小二乘回归

普通最小二乘回归

载入模块

import numpy as np
import statsmodels.api as sm

生成自变量数组，并生成设计矩阵

X = np.random.random((100, 2)) # 100 * 2 矩阵
X = sm.add_constant(X) # 左边一列加一列常数 -> 不过原点的线性回归
X

预定义好参数，生成因变量数据

$\beta$

beta = [1, .1, .5] # 3 * 1 矩阵
e = np.random.random(100) # 噪声
y = np.dot(X, beta) + 0.1*2
e, y

调用sm.OLS函数实现线性回归

results = sm.OLS(y, X).fit() # 拟合
print(results.summary()) # 回归拟合摘要

Dep.Variable : 使用的参数值  
Model：使用的模型
method：使用的方法
Data：时间
No.Observations：样本数据个数
Df Residuals：残差的自由度
DF Model：模型的自由度

R-squared：R方值
Adj.R-squared:调整后的R方
F-statistic: F统计量
Prob（F-statistic)：F统计量的p值
Log-Likelihood：似然度
AIC BIC：衡量模型优良度的指标，越小越好


coef: 系数
std err: 标准错误
t: t检验（t值）
P>|t|: t检验的p值，如果p值小于0.05 那么我们就认为变量是显著的
[0.025: 95%置信下限
0.975]: 95%置信上限 
 
const：截距项 （点估计）
x1, x2：自变量

Omnibus: 综合            
Prob(Omnibus): 概率              
Skew: 偏斜                       
Kurtosis: 峰度
  
 Durbin-Watson: 杜宾·沃森  
 Jarque-Bera (JB): Jarque-Bera
 Prob(JB): 概率      
 Cond. No.: 条件        

results.params # 回归系数

results.fittedvalues # 拟合y值

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111, projection='3d') #ax = Axes3D(fig)
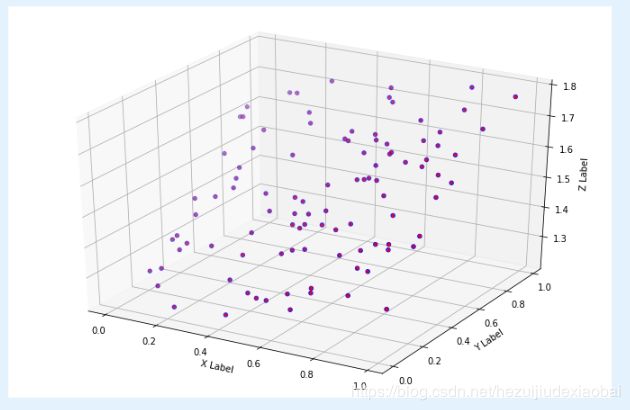
ax.scatter(X[:,1], X[:,2], y, c='b', marker='o')
ax.scatter(X[:,1], X[:,2], results.fittedvalues, c='r', marker='+')
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()

2.6.3 使用数据框&模型公式实现线性回归

载入相关模块

import numpy as np
import pandas as pd
import statsmodels.formula.api as smf

生成随机数作为自变量，然后产生因变量

x = np.random.random((100, 3))
y = 1 + 0.1*x[:,1] + 0.5*x[:,2] + 0.1*x[:,0]
x, y

生成字典型数据&数据框数据

mydict = {'x1': x[:,1], 'x2': x[:,2], 'y': y}
mydata = pd.DataFrame(mydict)
mydict
mydata

调用smf.ols实现线性回归

results = smf.ols(formula='y ~ x1+x2 ', data=mydata).fit()

2.6.4 其他

• ▶ 线性模型和广义线性模型等
• ▶ 线性混合效应模型
• ▶ 方差分析
• ▶ 时间序列模型
• ▶ 统计模型结果的可视化

2.7 Scikit-learn

• ▶ 实现数据降维、模型选择和数据预处理
• ▶ 用于分类、聚类、预测等数据挖掘和数据分析任务