【大话数据结构】树和二叉树

树的定义

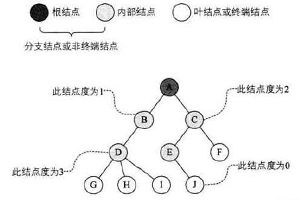
树（Tree）是n(n>=0)个结点的有限集。线性表是一对一的结构，而树则是一对多的结构。

定义条件：(1) 有且仅有一个根结点。(2) 子树的个数没有限制，但一定互不相交。

树的结点包含一个数据元素及若干个指向子树的分支。下图是结点分类：

树结构和线性结构的比较：

线性结构	树结构
第一个数据元素：无前驱	根结点：无父结点，唯一
最后一个数据元素：无后继	叶结点：无子结点，可以多个
中间元素：一个前驱一个后继	中间结点：一个父结点，多个子结点

树的存储表示法

【parent表示法】这种方法找到结点的父结点很容易，但想找子结点，就要靠遍历了。

data

parent

#define MAX_TREE_SIZE 100
typedef int TElemType;  //树结点的数据类型
typedef struct PTNode    //结点结构
{  
	TElemType data;
	int parent;       //父结点位置
}PTNode;
typedef struct		  //树结构
{
	PTNode nodes{MAX_TREE_SIZE};
	int r, n;         //根结点位置,结点数
}Tree;

【child表示法】这种方法找子结点容易，找父结点就不易了。

data

child1

child2

child3

...

childN

#define MAX_TREE_SIZE 100
typedef int TElemType; 
typedef struct CTNode    //子结点结构
{
	struct CTNode *next;
	int child;
}CTNode, *ChildPtr;
typedef struct		   //表头结构
{
	TElemType data;
	ChildPtr firstchild;
}CTChain;
typedef struct		  //树结构
{
	CTChain nodes{ MAX_TREE_SIZE };
	int r, n;         //根结点位置,结点数
}Tree;

二叉树及其存储

二叉树（binary tree）是一种特殊的树结构，特点是1.每个结点最多有2棵子树，2.左子树和右子树是有顺序的，3.即使某结点只有一棵子树也要区分它是左子树还是右子树。

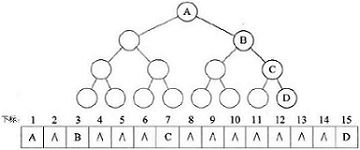
【顺序存储】一般用于完全二叉树。但有时会有下面情况：只有k个结点且深度为k的右斜树，却要分配 2^k-1 个存储单元，造成浪费。

【二叉链表】

lchild

data

rchild

typedef struct BiTNode 
{
	TElemType data;
	struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

二叉树的建立与遍历

二叉树的建立采用递归的方式，遍历也同样用递归原理来做。

二叉树的建立

// 构建二叉树, #表示空树
void BuildBiTree(BiTree T)
{
	TElemType data;
	scanf("Node data:%d", data);  //用户输入结点数据
	if (data == '#')
		T = NULL;
	else
	{
		T = (BiTree)malloc(sizeof(BiTNode));
		T->data = data;          //生成结点
		BuildBiTree(T->lchild);  //构造左子树
		BuildBiTree(T->rchild);  //构造右子树
	}
}

前序遍历

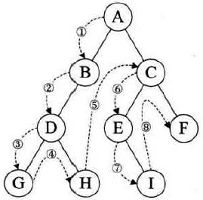
从根结点出发，前序遍历左子树，再前序遍历右子树。

void PreOrderTraverse(BiTree T)
{
	if (T == NULL)
		return;
	printf("node data: %d", T->data); //或是对结点的其他操作
	PreOrderTraverse(T->lchild);
	PreOrderTraverse(T->rchild);
}

中序遍历

从根结点的左子树开始，中序遍历每个结点的左子树，然后访问根结点，最后中序遍历右子树。

void InOrderTraverse(BiTree T)
{
	if (T == NULL)
		return;
	InOrderTraverse(T->lchild);
	printf("node data: %d", T->data); //或是对结点的其他操作
	InOrderTraverse(T->rchild);
}

后序遍历

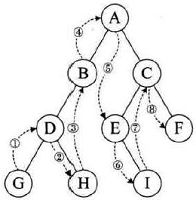
从左到右，先叶子后结点的方式访问左子树和右子树，最后是根结点。

void PostOrderTraverse(BiTree T)
{
	if (T == NULL)
		return;
	PostOrderTraverse(T->lchild);
	PostOrderTraverse(T->rchild);
	printf("node data: %d", T->data); //或是对结点的其他操作
}

PS：还有一个经典概念是赫夫曼树，以后补充。