大话数据结构-程杰著 数据结构树的学习(部分)
二叉树的遍历
1. 二叉树的遍历方法:
(图前序遍历)
可以利用栈的思想,将遍历的次序依次放入到栈中,如前序遍历(将根放入栈中,根节点出栈,打印根节点,然后再将右子节点、左子节点依次放入,然后再左子节点出栈进行打印,左子节点的右左节点在次入栈;根节点的所有左子树节点全部出栈后在执行根节点的右子树出栈进栈操作。)
这里的前中后序遍历,是以根节点为参考点来讲的,先根节点的为前序,先左节点根节点右节点的为中序,后续则是左右根。(只针对于前序遍历)
或者也可以说是遍历左、右节点,根节点放在最前面(左前序遍历和右前序遍历的前面)则是前序遍历;根节点处理放在(左中序遍历和右中序遍历的中间)则是中序遍历;根节点处理放在(左后续遍历和右后续遍历的后面)则是后续遍历。
(1) 前序遍历
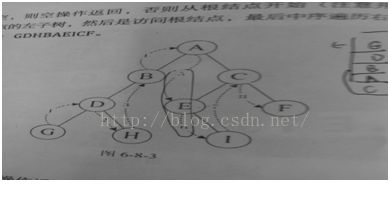
前序遍历规则:如果二叉树为空,则空操作返回;否则先访问根节点,然后前序遍历左子树,再遍历右子树,上图的顺序为前序遍历的次序:ABDGHCEIF
Void preSequence(Trees tree){
If tree is nullreturn ;
Else {
System.out.print(tree.node+””);
preSequence(tree.leftChild);
preSequence(tree.rightChild);
}
}
(2) 中序遍历
规则如果树为空,则返回;否则从根节点开始(并不是先访问根节点),中序遍历根节点的左子树,然后访问根节点,最后中序遍历右子树。GDHBAEICF
Void midSequence(Tree tree){
If tree is nullreturn ;
Else{
midSequence(tree.left);
System.out.println(tree.node);
midSequence(tree.right);
}
}
(3) 后序遍历
规则是如果树为空,则操作返回;否则从左到右先叶子后结点的方式遍历访问左右子树:上图的顺序是:GHDBIEFCA.
Void postSequence(Tree tree){//tree作为当前的借点
If tree is nullreturn;
Else {
postSequence(tree.left);
postSequence(tree.right);
System.out.println(tree.node);
}
}
(4) 层次遍历
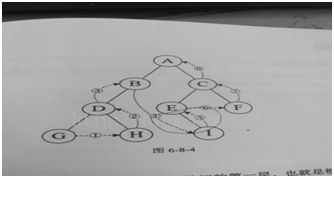
规则:如果树是空的,则返回;否则从树的第一层,也就是根节点开始访问,从上而下逐层遍历,在同一层中安从左到右对节点顺序访问。上图:ABCDEFGHI
Void hierchSequence(Tree tree){
If tree is nullreturn ;
Else{
hierchSequence(tree.left);
hierchSequence(tree.right);
}
}
赫夫曼树及其应用:
这里提及到了学生成绩按照60,70,80,90划分不及格,及格,中等,良好,优秀的登记,如果按照
If(score<60){}
Else if (score<70){}
Else if(score<80){}
Else if(score<90){}
{}
这样操作,如果数据量很大时,可能其效率会很低。想想有什么办法可以改变那?
我们知道一般从统计学来讲,成绩的分布应该是中间多,两头少的分布,如正太分布等,这样比如学生成绩在中等、良好的情况占大多数,这是我们可以以中等或者良好的分数来区分,如下图:
感觉在比较上应该是进行了优化的了。这种变换,其实和霍夫曼的定义吻合。
霍夫曼树,带权路径长度最小的二叉树。(最优二叉树)
路径长度为树中一个结点到另一个结点的分支构成了两个结点质检的路径,路径上的分支数目称为路径长度。
树的路径长度就是从树根到每一结点的路径长度之和。