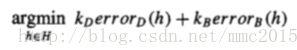《Machine Learning(Tom M. Mitchell)》读书笔记——13、第十二章
1. Introduction (about machine learning)
2. Concept Learning and the General-to-Specific Ordering
3. Decision Tree Learning
4. Artificial Neural Networks
5. Evaluating Hypotheses
6. Bayesian Learning
7. Computational Learning Theory
8. Instance-Based Learning
9. Genetic Algorithms
10. Learning Sets of Rules
11. Analytical Learning
12. Combining Inductive and Analytical Learning
13. Reinforcement Learning
12. Combining Inductive and Analytical Learning
Purely inductive learning methods formulate general hypotheses by finding empirical(经验化的) regularities over the training examples. Purely analytical methods use prior knowledge to derive general hypotheses deductively., This chapter considers methods that combine inductive and analytical mechanisms to obtain the benefits of both approaches: better generalization accuracy when prior knowledge is available and reliance(rely) on observed training data to overcome shortcomings in prior knowledge. The resulting combined methods outperform both purely inductive and purely analyti- cal learning methods. This chapter considers inductive-analytical learning methods based on both symbolic and artificial neural network representations.
12.1 MOTIVATION
What criteria should we use to compare alternative approaches to combining inductive and analytical learning? Some specific properties we would like from such a learning method include(Notice this list of desirable properties is quite ambitious):
12.2 INDUCTIVE-ANALYTICAL APPROACHES TO LEARNING(学习的归纳-分析途径)
12.2.1 The Learning Problem
What precisely shall we mean by "the hypothesis that best fits the training examples and domain theory?'.
For example, we could require the hypothesis that minimizes some combined measure of these errors, such as:
An alternative perspective on the question of how to weight prior knowl- edge and data is the Bayesian perspective. Recall from Chapter 6 that Bayes theorem describes how to compute the posterior probability P(h1D) of hypothe- sis h given observed training data D. Unfortunately, Bayes theorem implicitly assumes pe$ect knowledge about the probability distributions P(h), P(D), and P(Dlh). When these quantities are only imperfectly known, Bayes theorem alone does not prescribe how to combine them with the observed data.
We will revisit the question of what we mean by "best" fit to the hypothesis and data as we examine specific algorithms. For now, we will simply say that the learning problem is tominimize some combined measure of the error of the hypothesis over the data and the domain theory.
12.2.2 Hypothesis Space Search
One way to understand the range of possible approaches is to return to our view of learning as a task of searching through the space of alternative hypotheses. We can characterize most learning methods as search algorithms by describing the hypothesis space H they search, the initial hypothesis ho at which they begin their search, the set of search operators 0 that define individual search steps, and the goal criterion G that specifies the search objective.
In this chapter we explore three different methods for using prior knowledge to alter the search performed by purely inductive methods:
Use prior knowledge to derive an initial hypothesis from which to begin the search. In this approach the domain theory B is used to construct an initial hypothesis ho that is consistent with B. A standard inductive method is then applied, starting with the initial hypothesis ho.
Use prior knowledge to alter the objective of the hypothesis space search. In this approach, the goal criterion G is modified to require that the output hypothesis fits the domain theory as well as the training examples.
Use prior knowledge to alter the available search steps. In this approach, the set of search operators 0 is altered by the domain theory.
12.3 USING PRIOR KNOWLEDGE TO INITIALIZE THE HYPOTHESIS(用先验知识得到初始假设)
It is easy to see the motivation for this technique: if the domain theory is correct, the initial hypothesis will correctly classify all the training examples and there will be no need to revise it. However, if the initial hypothesis is found to imperfectly classify the training examples, then it will be refined inductively to improve its fit to the training examples.
12.3.1 The KBANN Algorithm
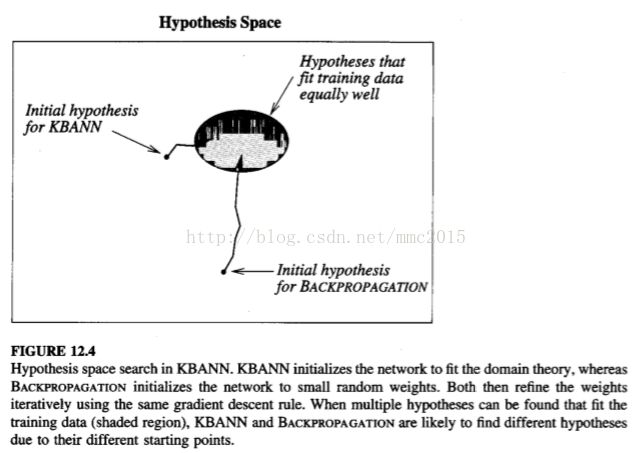
The two stages of the KBANN algorithm are first to create an artificial neural network that perfectly fits the domain theory and second to use the BACKPROPA-CATION algorithm to refine this initial network to fit the training examples. The details of this algorithm, including the algorithm for creating the initial network, are given in Table 12.2 and illustrated in Section 12.3.2.
12.3.2 An Illustrative Example
12.3.3 Remarks
The chief benefit of KBANN over purely inductive BACKPROPAGATION (beginning with random initial weights) is that it typically generalizes more accurately than BACKPROPAGATION when given an approximately correct domain theory, es- pecially when training data is scarce.
Limitations of KBANN include the fact that it can accommodate only propositional domain theories; that is, collections of variable-free Horn clauses. It is also possible for KBANN to be misled when given highly inaccurate domain theories, so that its generalization accuracy can deteriorate below the level of BACKPROPA-GATION. Nevertheless, it and related algorithms have been shown to be useful for several practical problems.
12.4 USING PRIOR KNOWLEDGE TO ALTER THE SEARCH OBJECTIVE(使用先验知识改变搜索目标)
An alternative way of using prior knowledge is to incorporate it into the error criterion minimized by gradient descent, so that the network must fit a combined function of the training data and domain theory. In this section, we consider using prior knowledge in this fashion. In particular, we consider prior knowledge in the form of known derivatives of the target function.
12.4.1 The TANGENTPROP Algorithm
The modified error function is:
12.4.3 Remarks
Although TANGENTPROP succeeds in combining prior knowledge with train- ing data to guide learning of neural networks, it is not robust to errors in the prior knowledge. Consider what will happen when prior knowledge is incorrect, that is, when the training derivatives input to the learner do not correctly reflect the derivatives of the true target function. In this case the algorithm will attempt to fit incorrect derivatives. It may therefore generalize less accurately than if it ignored this prior knowledge altogether and used the purely inductive BACKPROPAGATION algorithm. If we knew in advance the degree of error in the training derivatives, we might use this information to select the constant p that determines the relative importance of fitting training values and fitting training derivatives. However, this information is unlikely to be known in advance.
It is interesting to compare the search through hypothesis space (weight space) performed by TANGENTPROP, KBANN, and BACKPROPAGATION.
12.4.4 The EBNN Algorithm
12.4.5 Remarks
To summarize, the EBNN algorithm uses a domain theory expressed as a set of previously learned neural networks, together with a set of training examples, to train its output hypothesis (the target network). For each training example EBNN uses its domain theory to explain the example, then extracts training derivatives from this explanation. For each attribute of the instance, a training derivative is computed that describes how the target function value is influenced by a small change to this attribute value, according to the domain theory. These training derivatives are provided to a variant of TANGENTPROP, which fits the target network to these derivatives and to the training example values. Fitting the derivatives constrains the learned network to fit dependencies given by the domain theory, while fitting the training values constrains it to fit the observed data itself. The weight pi placed on fitting the derivatives is determined independently for each training example, based on how accurately the domain theory predicts the training value for this example.
EBNN bears an interesting relation to other explanation-based learning methods, such as PROLOG-EBGde scribed in Chapter 11.
There are several differences in capabilities between EBNN and the symbolic explanation-based methods of Chapter 11. The main difference is that EBNN accommodates imperfect domain theories, whereas PROLOG-EBGdo es not. This difference follows from the fact that EBNN is built on the inductive mechanism of fitting the observed training values and uses the domain theory only as an additional constraint on the learned hypothesis. A second important difference follows from the fact that PROLOG-EBGle arns a growing set of Horn clauses, whereas EBNN learns a fixed-size neural network. As discussed in Chapter 11, one difficulty in learning sets of Horn clauses is that the cost of classifying a new instance grows as learning proceeds and new Horn clauses are added. This problem is avoided in EBNN because the fixed-size target network requires constant time to classify new instances. However, the fixed-size neural network suffers the corresponding disadvantage that it may be unable to represent sufficiently complex functions, whereas a growing set of Horn clauses can represent increasingly complex functions.
12.5 USING PRIOR KNOWLEDGE TO AUGMENT SEARCH OPERATORS(使用先验知识来扩展搜索算子)
In this section we consider a third way of using prior knowledge to alter the hypothesis space search: using it to alter the set of operators that define legal steps in the search through the hypothesis space.
12.5.1 The FOCL Algorithm
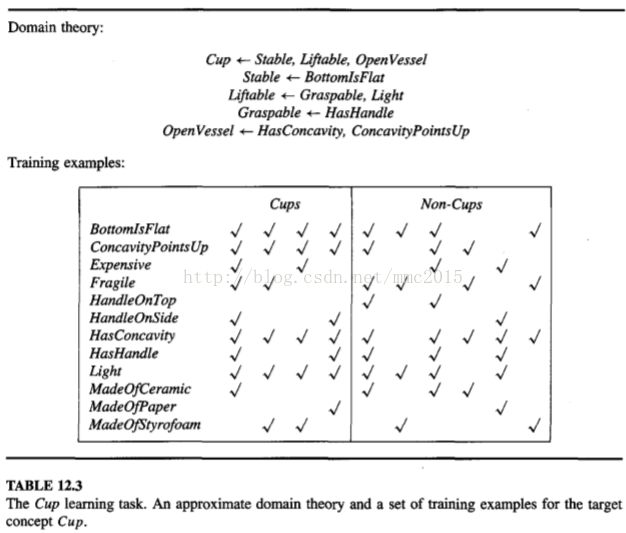
We will say a literal is operational if it is allowed to be used in describing an output hypothesis. For example, in the Cup example of Figure 12.3 we allow output hypotheses to refer only to the 12 attributes that describe the training examples (e.g., HasHandle, HandleOnTop). Literals based on these 12 attributes are thus considered operational. In contrast, literals that occur only as intermediate features in the domain theory, but not as primitive attributes of the instances, are considered nonoperational. An example of a nonoperational attribute in this case is the attribute Stable.
At each point in its general-to-specific search, FOCL expands its current hypothesis h using the following two operators:
For each operational literal that is not part of h, create a specialization of h by adding this single literal to the preconditio s. This is also the method used by FOIL to generate candidate successors. he solid arrows in Figure 12.8 denote this type of specialization.
Create an operational, logically sufficient condition for the target concept according to the domain theory. Add this set of literals to the current precon- ditions of h. Finally, prune the preconditions of h by removing any literals that are unnecessary according to the training data. The dashed arrow in Figure 12.8 denotes this type of specialization.
Once candidate specializations of the current hypothesis have been generated, using both of the two operations above, the candidate with highest informa- tion gain is selected.
12.5.2 Remarks
To summarize, FOCL uses both a syntactic generation of candidate specializations and a domain theory driven generation of candidate specializations at each step in the search. The algorithm chooses among these candidates based solely on their empirical support over the training data. Thus, the domain theory is used in a fashion that biases the learner, but leaves final search choices to be made based on performance over the training data. The bias introduced by the domain theory is a preference in favor of Horn clauses most similar to operational, logically sufficient conditions entailed by the domain theory. This bias is combined with the bias of the purely inductive FOIL program, which is a preference for shorter hypotheses.
FOCL has been shown to generalize more accurately than the purely inductive FOIL algorithm in a number of application domains in which an imperfect do- main theory is available.
12.7 SUMMARY AND FURTHER READING
Approximate prior knowledge, or domain theories, are available in many practical learning problems. Purely inductive methods such as decision tree induction and neural network BACKPROPAGATION fail to utilize such domain theories, and therefore perform poorly when data is scarce. Purely analytical learning methods such as PROLOG-EBG utilize such domain theories, but produce incorrect hypotheses when given imperfect prior knowledge. Methods that blend inductive and analytical learning can gain the benefits of both approaches: reduced sample complexity and the ability to overrule incorrect prior knowledge.
One way to view algorithms for combining inductive and analytical learning is to consider how the domain theory affects the hypothesis space search. In this chapter we examined methods that use imperfect domain theories to (1) create the initial hypothesis in the search, (2) expand the set of search operators that generate revisions to the current hypothesis, and (3) alter the objective of the search.
A system that uses the domain theory to initialize the hypothesis is KBANN. This algorithm uses a domain theory encoded as propositional rules to analytically construct an artificial neural network that is equivalent to the domain theory. This network is then inductively refined using the BACKPROPAGATION algorithm, to improve its performance over the training data. The result is a network biased by the original domain theory, whose weights are refined inductively based on the training data.
TANGENTPROP uses prior knowledge represented by desired derivatives of the target function. In some domains, such as image processing, this is a natural way to express prior knowledge. TANGENTPROP incorporates this knowledge by altering the objective function minimized by gradient descent search through the space of possible hypotheses.
EBNN uses the domain theory to alter the objective in searching the hypothesis space of possible weights for an artificial neural network. It uses a domain theory consisting of previously learned neural networks to perform a neural network analog to symbolic explanation-based learning. As in symbolic explanation-based learning, the domain theory is used to explain individual examples, yielding information about the relevance of different example features. With this neural network representation, however, information about relevance is expressed in the form of derivatives of the target function value with respect to instance features. The network hypothesis is trained using a variant of the TANGENTPROP algorithm, in which the error to be minimized includes both the error in network output values and the error in network derivatives obtained from explanations.
FOCL uses the domain theory to expand the set of candidates considered at each step in the search. It uses an approximate domain theory represented by first order Horn clauses to learn a set of Horn clauses that approximate the target function. FOCL employs a sequential covering algorithm, learning each Horn clause by a general-to-specific search. The domain theory is used to augment the set of next more specific candidate hypotheses considered at each step of this search. Candidate hypotheses are then evaluated based on their performance over the training data. In this way, FOCL combines the greedy, general-to-specific inductive search strategy of FOIL with the rule-chaining, analytical reasoning of analytical methods.
The question of how to best blend prior knowledge with new observations remains one of the key open questions in machine learning.