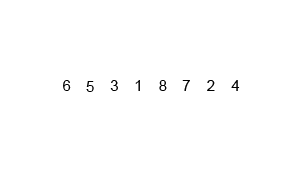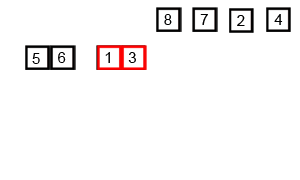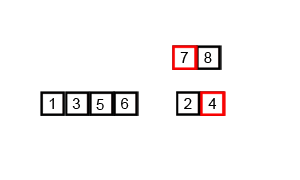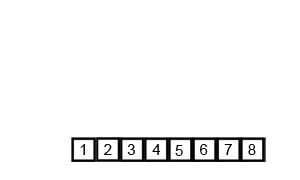一、归并排序
-
所谓“分”,指的是将一个乱序数列不断进行二分,得到许多短的序列。
-
所谓“治”,指的是将这些短序列进行两两合并,然后将合并的结果作为新的序列,再与其他序列进行合并,最终得到一个新的序列。
归并排序算法描述
-
把长度为n的输入序列分成两个长度为n/2的子序列;
-
对这两个子序列分别采用归并排序;
-
将两个排序好的子序列合并成一个最终的排序序列。
归并排序动图演示
动画演示图2
归并排序代码实现
def merge_sort(alist):
"""归并排序"""
n = len(alist)
#递归结束条件
# 剩一个或没有直接返回,不用排序
if n <= 1:
return alist
# 拆分
mid = n//2
# left 采用归并排序后形成的有序的新的列表
left_li = merge_sort(alist[:mid])
# right 采用归并排序后形成的有序的新的列表
right_li = merge_sort(alist[mid:])
# 将两个有序的子序列合并为一个新的整体
# merge(left, right)
left_pointer, right_pointer = 0, 0
result = []
while left_pointer < len(left_li) and right_pointer < len(right_li):
if left_li[left_pointer] <= right_li[right_pointer]:
result.append(left_li[left_pointer])
left_pointer += 1
else:
result.append(right_li[right_pointer])
right_pointer += 1
#将两个列表按顺序融合为一个列表result
result += left_li[left_pointer:]
result += right_li[right_pointer:]
return result
归并排序过程分析
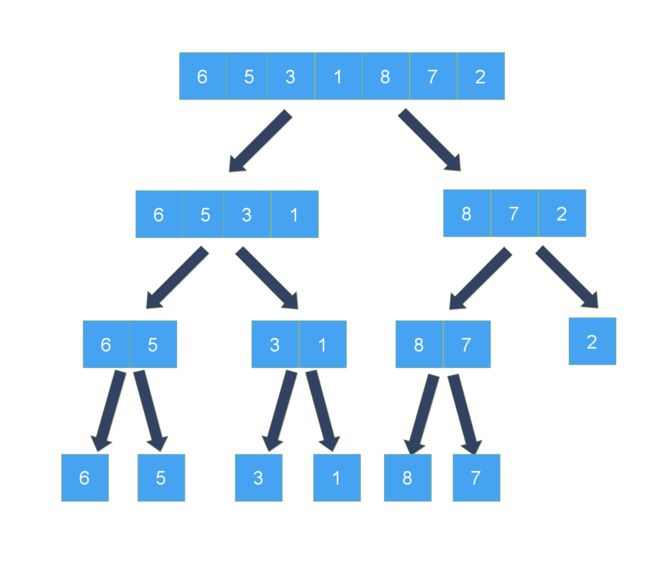
示例 针对 arrli = [6,5,3,1,8,7,2,4]进行归并排序
1、拆分数组
假设数组一共有 n 个元素,我们递归对数组进行折半拆分即n//2,直到每组只有一个元素为止。
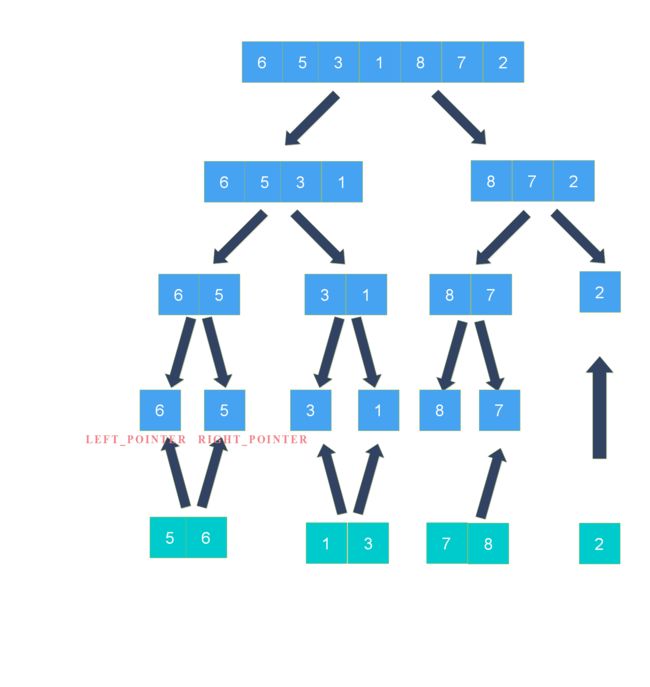
2、合并数组
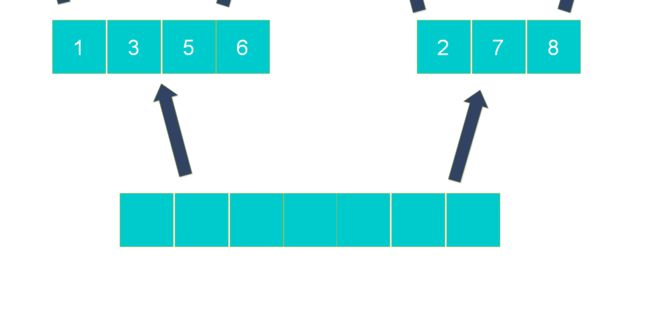
算法会从最小数组开始有序合并,这样合并出来的数组一直是有序的,所以合并两个有序数组是归并算法的核心,这里用两个简单数组示例:
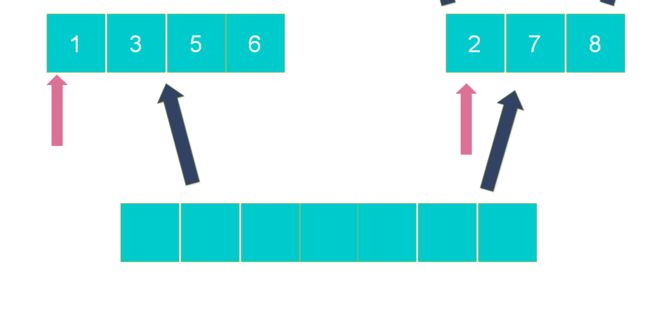
步骤1:新建一个空数组存放合并结果,用left_pointer和right_pointer两个辅助指针记录两个数组当前操作位置;
步骤2:从左到右逐一比较两个小数组中的元素,较小的元素先放入新数组,指针移位,直到left_pointer和right_pointer指针超出尾部;
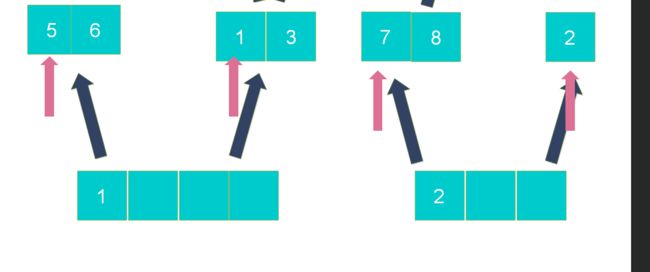
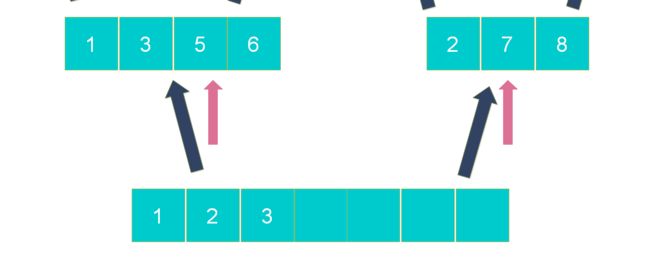
步骤3:新建一个空数组存放合并结果,用l和r两个辅助指针记录两个数组当前操作位置;
步骤4:从左到右逐一比较两个小数组中的元素,较小的元素先放入新数组,指针移位,直到l或r指针超出尾部;
继续比较写入较小的元素到新数组
继续比较写入较小的元素到新数组
指针尚未移到尾部的数组,说明还有剩余元素,将剩余元素合并到新数组尾部。
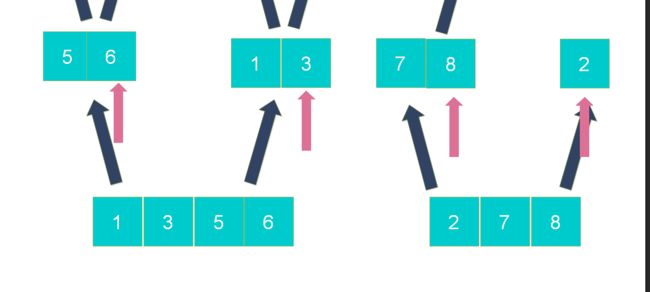
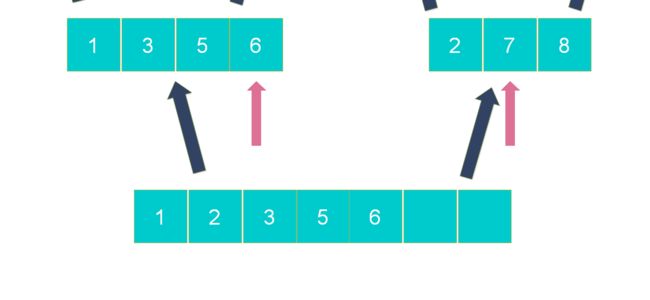
步骤5:新建一个空数组存放合并结果,用l和r两个辅助指针记录两个数组当前操作位置;
步骤6:从左到右逐一比较两个小数组中的元素,较小的元素先放入新数组,指针移位,直到l或r指针超出尾部;
将较小的元素写入到新数组
继续比较写入较小的元素到新数组
继续比较写入较小的元素到新数组
继续比较写入较小的元素到新数组
步骤7:右边的指针尚未移到尾部的数组,说明还有剩余元素,将剩余元素合并到新数组尾部。
完成归并排序,返回排好序的新数组
归并排序复杂度
-
时间复杂度:O(nlogn)
归并排序把数组一层层折半分组,长度为 n 的数组,折半层数就是 logn,每一层进行操作的运算量是 n,得出时间复杂度 O(nlogn)。
-
空间复杂度:O(n)
每次归并操作需要创建额外的新数组,占用空间为 n,但这部分额外空间会随着方法的结束而释放,所以只需要算单次归并操作开辟的空间即可,得出空间复杂度 O(n)。
-
稳定性:稳定
从算法中从左到右逐一比较,较小的先放入新数组,所以两个值相同的元素,排序后依然保持原先后顺序。