Python数据分析基础技术之Scipy

scipy是一个用于数学、科学、工程领域的常用软件包，可以处理插值、积分、优化、图像处理、常微分方程数值解的求解、信号处理等问题。它用于有效计算Numpy矩阵，使Numpy和Scipy协同工作，高效解决问题。

scipy官网：https://www.scipy.org/ 学习过程中可以查询官方文档

Scipy是由针对特定任务的子模块组成：

模块名	应用领域
scipy.io	数据输入输出
scipy.integrate	积分程序
scipy.interpolate	插值
scipy.linalg	线性代数程序
scipy.optimize	优化
scipy.cluster	向量计算/Kmeans
scipy.constants	物理和数学常量
scipy.fftpack	傅立叶变换
scipy.ndimage	n维图像包
scipy.odr	正交距离回归
scipy.signal	信号处理
scipy.sparse	稀疏矩阵
scipy.spatial	空间数据结构和算法
scipy.special	一些特殊的数学函数
scipy.stats	统计

1. 积分（scipy.integrate）

导入模块：

from scipy.integrate import quad,dblquad,nquad    #一维积分，二维积分，n维积分

print(quad(lambda x: np.exp(-x), 0, np.inf))   #exp（x）是e为底的指数函数

print(dblquad(lambda t, x: np.exp(-x * t) / t ** 3, 0, np.inf, lambda x: 1, lambda x: np.inf))  #**表示幂运算

#n元积分
def f(x,y):
    return x*y
def bound_y():
    return [0,0.5]
def bound_x(y):
    return [0,1-2*y]
print(nquad(f,[bound_x,bound_y]))

结果是返回一个值和误差组成的元组

2. 优化（scipy.optimize）

scipy.optimize模块提供了函数最值、曲线拟合和求根的算法。

该模块包括：
——多元标量函数的无约束和约束极小化(minimize)。使用多种算法(例如BFGS、Nder-Mead单纯形、Newton共轭梯度、COBYLA或SLSQP)
——全局(蛮力)优化例程。basinhopping, differential_evolution)
——最小二乘极小化(least_squares)和曲线拟合(curve_fit)算法
——标量单变量函数极小化(minimize_scalar)和根查找器(root_scalar)
——多元方程组求解器(root)使用多种算法(例如，混合鲍威尔、Levenberg-MarQuardt或大规模方法，如Newton-Krylov)

无约束函数最值(以最小值为例)：
导入模块：

from scipy.optimize import minimize
import numpy as np

在数学最优化中，Rosenbrock函数是一个用来测试最优化算法性能的非凸函数，由Howard Harry Rosenbrock在1960年提出。也称为Rosenbrock山谷或Rosenbrock香蕉函数，也简称为香蕉函数。
函数表达式（N是x的维数）：

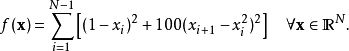
定义一个目标函数（Rosenbrock函数——香蕉函数）：

def rosen(x):
    """The Rosenbrock function"""
    return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0+(1-x[:-1])**2.0)
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])

求解：

res = minimize(rosen, x0, method='nelder-mead', options={'xtol': 1e-8, 'disp': True})
 print（res.x）     #res.x是优化结果，返回一个ndarry

minimize(fun, x0[, args, method, jac, hess, …])
fun——一个或多个变量的标量函数的最小化
x0——初始猜测值，相当于指定了N
method就是优化算法
Xtol是精度
disp指是否显示过程（True则显示）

过程与结果：

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 339
         Function evaluations: 571
[1. 1. 1. 1. 1.]

有约束函数最值（最小值为例）：
导入模块：

from scipy.optimize import minimize
import numpy as np

定义函数：
f(x) = 2xy+2x-x²-2y²
偏导数：
2y+2-2x
2x-4y

def fun(x):
    return (2*x[0]*x[1]+2*x[0]-x[0]**2-2*x[1]**2)
def func_deriv(x):
    dfdx0 = (-2*x[0]+2*x[1]+2)
    dfdx1 = (2*x[0]-4*x[1])
    return np.ndarry([dfdx0,dfdx1])

约束条件(等于转化为=0和不等于转化为>=0):

3x²-y = 0
y-1>=0

cons = ({"type":"eq","fun":lambda x;np.ndarray([x[0]**3-x[1]]),"jac":lamda x;np.ndarray([3*(x[0]**2),-1])}
         ,{"type":"ineq","fun":lambda x;np.ndarray([x[1]-1]),"jac":lamda x;np.ndarray(0,1])})         

雅可比矩阵是函数的一阶偏导数以一定方式排列成的矩阵，其行列式称为雅可比行列式。
求解：

x0 = np.array([-1.0, 1.0])
>>> res = minimize(func, x0, method='SLSQP', jac=func_deriv,constraints=cons, options={'disp': True})       #顺序最小二乘规划(SLSQP)算法(method='SLSQP')
print(res.x)

结果：

x：array([1.0000009,1])

优化器求根：
导入模块：

from scipy.optimize import root
import numpy as np

定义函数：
x+2cos（x） = 0

def func(x):
    return x + 2 * np.cos(x)

求解和结果：

sol = root(func, 0.1)   #root（fun,x0)，fun为函数，x0是Initial guess.（初始猜测值）
print（sol.x） #优化（根）结果
>>array([-1.02986653])
print（sol.fun）     #目标函数的值
>>array([ -6.66133815e-16])

3. 插值（scipy.interpolate）：

插值是在离散数据的基础上补插连续函数，使得这条连续曲线（连续函数）通过全部给定的离散数据点，从而由连续曲线估算出在其他点处的近似值

导入模块：

 from scipy.interpolate import interp1d       #一维插值interp1d
 impory numpy as np 
 from pylab import *        #pylab的模块，其中包括了许多NumPy和pyplot模块中常用的函数，方便用户快速进行计算和绘图

定义离散数据：

x = np.linspace(0,1,10)
y = np.sin(2*np.pi*x)

插值：

li = interp1d(x,y,kind="cubic")      #x和y用于近似某些函数f的值数组：y = f(x)。该类返回一个函数
x_new = np.linspace(0,1,50)
y_new = li(x_new)        #函数的调用方法使用插值来查找新点的值

画出结果（如下图）：

figure()      
plot(x,y,"r")      #red为离散数据
plot(x_new,y_new,"k")    #黑色为插值后的数据

4. 线性计算和矩阵分解（scipy.linalg）：
使用scipy处理矩阵和numpy是一样的
导入模块：

from scipy import linalg as llg

计算：

arr=np.array([[1,2],[3,4]])
llg.det(arr)      #行列式值
llg.inv(arr)      #转置
b=np.array([8,14])
llg.solve(arr,b)     #解方程组x+2y=8 and 3x+4y=14
llg.eig(arr)     #求特征值
llg.lu(arr)       #矩阵的Lu分解
llg.qr(arr)       #矩阵的qr分解
llg.svd(arr)     #矩阵的svd分解
llg.schur(arr)     #矩阵的舒尔（schur）分解

补充矩阵分解知识：*

矩阵分解 (decomposition, factorization)是将矩阵拆解为数个矩阵的乘积，常见的有三种：1)三角分解法 (Triangular Factorization)（Lu分解），2)QR 分解法 (QR Factorization)，3)奇异值分解法 (Singular Value Decomposition)。

——三角分解法是将原正方 (square) 矩阵分解成一个上三角形矩阵或是排列(permuted) 的上三角形矩阵和一个 下三角形矩阵，这样的分解法又称为LU分解法

——QR分解法是将矩阵分解成一个正规正交矩阵与上三角形矩阵,所以称为QR分解法

——奇异值分解 (singular value decomposition,SVD) 是另一种正交矩阵分解法；SVD是最可靠的但比QR 分解法耗费近10倍的计算时间。[U,S,V]=svd(A)，其中U和V分别代表两个正交矩阵，而S代表一对角矩阵。 和QR分解法相同， 原矩阵A不必为正方矩阵。使用SVD分解法的用途是解最小平方误差法和数据压缩。*

Scipy的基础知识与操作就到这里，如果需要更深入学习scipy，官网的教程是个很好的选择，接下来让我们一起了解Pandas常见用法（点击进入)