利用栈的结构实现四则运算

设计一个C语言程序，演示用算符优先法对算术表达式求值的过程。利用算符优先关系，实现对算术四则混合运算表达式的求值。
包含的运算符只能有’+’ 、’-’ 、’*’ 、’/’ 、’(’、 ‘)’，“=”代表输入结束符；
为了实现用栈计算算数表达式的值，需设置两个工作栈：用于存储运算符的栈opter，以及用于存储操作数及中间结果的栈opnd。
算法基本思想如下：
（1）首先将操作数栈opnd设为空栈，而将’#‘作为运算符栈opter的栈底元素，这样的目的是判断表达式是否求值完毕。
（2）依次读入表达式的每个字符，表达式须以’#‘结尾，若是操作数则入栈opnd，若是运算符,则将此运算符c与opter的栈顶元素top比较优先级后执行相应的操作，具体操作如下：
(i)若top的优先级小于c，即top (ii)若top的优先级等于c，即top=c，则弹出opter的才顶元素，并读入下一字符赋值给c，这一步目的是进行括号操作;
（iii）若top优先级高于c，即top>c，则表明可以计算，此时弹出opnd的栈顶两个元素，并且弹出opter栈顶的的运算符，计算后将结果放入栈opnd中。直至opter的栈顶元素和当前读入的字符均为’#’，此时求值结束。
算符间的优先关系如下表所示（表来源：严蔚敏《数据结构》）：

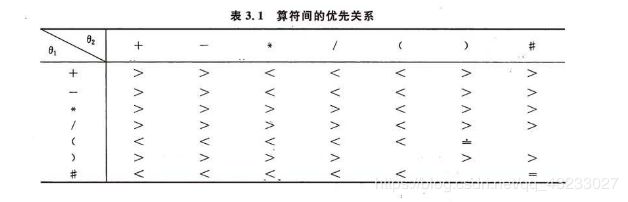
表中需要注意的是θ1为opter的栈顶元素，θ2为从表达式中读取的操作符，此优先级表可以用二维数组实现。
完整代码：

#include
#include
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
#define STACK_INIT_SIZE 100 //存储空间初始分配量
#define STACKINCREMENT 10 //存储空间分配增量

typedef char SElemType;
typedef char OperandType; //表达式求值的运算类型
typedef int Status;

typedef struct
{
SElemType *base;
SElemType *top;
int stacksize;
}SqStack;

//构造一个空栈
Status InitStack(SqStack *S)
{
S->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
if(!S->base)
{
printf(“内存分配失败!\n”);
exit(OVERFLOW);
}

S->top = S->base;
S->stacksize = STACKINCREMENT;
return OK; 

}

//若栈不为空，则用e返回S的栈顶元素，并返回OK；否则返回ERROR
Status GetTop(SqStack *S, SElemType *e)
{
if(S->top == S->base)
return ERROR;

*e = *(S->top - 1);
return OK;

}

//插入元素e为新的栈顶元素
Status Push(SqStack *S, SElemType e)
{
if(S->top - S->base >= STACK_INIT_SIZE) //栈满， 追加存储空间
{
S->base = (SElemType *)realloc(S->base, (S->stacksize + STACKINCREMENT) * sizeof(SElemType));
if(!S->base)
{
printf(“内存分配失败!\n”);
exit(OVERFLOW);
}

    S->top = S->base + S->stacksize;
    S->stacksize += STACKINCREMENT;
}

*S->top++ = e;

return OK;

}

//若栈不为空，则删除S的栈顶元素，用e返回其值，并返回Ok；否则返回ERROR
Status Pop(SqStack *S, SElemType *e)
{
if(S->top == S->base)
return ERROR;

*e =  *--S->top;

return OK;

}
//销毁栈S，使其不复存在
Status StackDestroy(SqStack *S)
{
free(S->base);
S->base = NULL;
S->top = NULL;
S->stacksize = 0;
return OK;
}

//清空栈S，保留栈底指针
void ClearStack(SqStack *S)
{
S->top = S->base;
}

//判断两符号的优先关系
char Precede(char t1, char t2){
int i,j;
char pre[][7]={
//运算符之间的优先级制作成一张表格
{’>’,’>’,’<’,’<’,’<’,’>’,’>’},
{’>’,’>’,’<’,’<’,’<’,’>’,’>’},
{’>’,’>’,’>’,’>’,’<’,’>’,’>’},
{’>’,’>’,’>’,’>’,’<’,’>’,’>’},
{’<’,’<’,’<’,’<’,’<’,’=’,‘0’},
{’>’,’>’,’>’,’>’,‘0’,’>’,’>’},
{’<’,’<’,’<’,’<’,’<’,‘0’,’=’}};
switch(t1){
case ‘+’: i=0; break;
case ‘-’: i=1; break;
case ‘’: i=2; break;
case ‘/’: i=3; break;
case ‘(’: i=4; break;
case ‘)’: i=5; break;
case ‘=’: i=6; break;
}
switch(t2){
case ‘+’: j=0; break;
case ‘-’: j=1; break;
case '’: j=2; break;
case ‘/’: j=3; break;
case ‘(’: j=4; break;
case ‘)’: j=5; break;
case ‘=’: j=6; break;
}
return pre[i][j];
}
//判断c是否为运算符
Status In(OperandType c)
{
switch©
{
case ‘+’:
case ‘-’:
case ‘*’:
case ‘/’:
case ‘(’:
case ‘)’:
case ‘=’:
return TRUE;
default:
return FALSE;
}

}

//二元运算(a theta b)
OperandType Operate(OperandType a, OperandType theta, OperandType b)
{
OperandType c;
switch(theta)
{
case ‘+’:
c = a + b;
break;
case ‘-’:
c = a - b;
break;
case ‘*’:
c = a * b;
break;
case ‘/’:
c = a / b;
break;
}
return c;
}

//算术表达式求值的算符优先算法，设OPTR和OPND分别为运算符栈和运算数栈，OP为运算符集合
OperandType EvaluateExpression()
{
SqStack OPTR, OPND;
OperandType a, b, d, x, theta;
char c; //存放有键盘输入的字符串
char z[6]; //存放整数字符串
int i;
InitStack(&OPTR); //初始化运算符栈
Push(&OPTR, ‘=’); //=是表达式结束符
InitStack(&OPND); //初始化运算数栈

c = getchar();
GetTop(&OPTR, &x);
while(c != '=' || x != '=')
{
    if(In(c))   //是7种运算符之一
    {
        switch(Precede(x, c))
        {
        case '<':   //当前已经压栈一个运算符（x）比后一个运算符（c）低时，就将c压栈
            Push(&OPTR, c);
            c = getchar();
            break;
        case '=':
            Pop(&OPTR, &x);   //脱括号并接收下一字符
            c = getchar();
            break;
        case '>':
            Pop(&OPTR, &theta);   //退栈并将运算结果压入OPND中
            Pop(&OPND, &b);
            Pop(&OPND, &a);
            Push(&OPND, Operate(a, theta, b));
            break;
        }
    }
        else if(c >= '0' && c <= '9')   //c是操作数
        {
            i = 0;
            do
            {
                z[i] = c;
                i ++;
                c = getchar();
            }while(c >= '0' && c <= '9');
            z[i] = 0;
            d = atoi(z);   //将字符数组转为整型存于d
            Push(&OPND, d);
        }
        else   //c为非法字符
        {
            printf("ERROR3\n");
            exit(1);
        }
        GetTop(&OPTR, &x);
    }
GetTop(&OPND, &x);
StackDestroy(&OPTR);
StackDestroy(&OPND);
return x;

}

int main()
{
printf(“请输入算术表达式，负数要用（0-正数），并以=结束:\n”);
printf("%d\n", EvaluateExpression());
return 0;
}