acm新手小白必看系列之（9）——栈精讲及例题

acm新手小白必看系列之（9）——栈精讲及例题

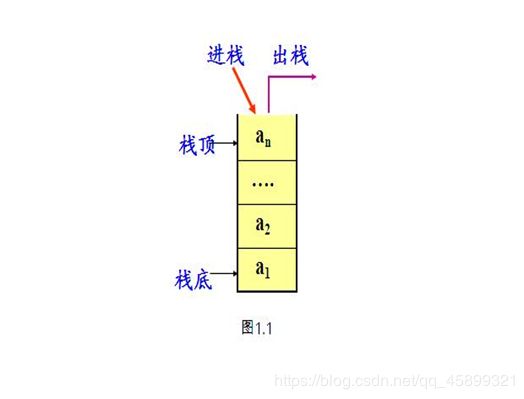先进栈后出栈
可以把栈想象成一个上端开口的杯子。。。。
栈只能定义为在一端进行插入和删除操作

1.程序员问题
程序员输入程序出现差错时，可以采取以下的补救措施：按错了一个键时，可以补按一个退格符“#”，以表示前一个字符无效；发现当前一行有错，可以按一个退行符“@”，以表示“@”与前一个换行符之间的字符全部无效。
Input
输入一行字符，个数不超过 100。
Output
输出一行字符，表示实际有效字符。
Sample Input
sdfosif@for (ii#=1,#;i<.#=8;i+++#);
Sample Output
for (i=1;i<=8;i++);
Hint
例子输入2：1234##
例子输出2：12

#include 
#include 
#include 
#include //万能头文件
using namespace std;

int main()
{
    stack <char> s1;//定义一个栈
    stack <char> s2;
    char str[110];
    gets(str);//输入
    int len=strlen(str);//长度函数
    for(int i=0; i<len; i++)
    {
        if(str[i]=='@')
        {
            while(!s1.empty())//判断是否为空
            //while(!s1)的意思是当!s1为真时循环，否则跳出循环。
            {
                s1.pop();//出栈将@之前的字符制空
            }
            continue;//全部制空后继续
        }
        if(str[i]=='#')
        {
            if(!s1.empty())
            {
                s1.pop();
                continue;//只制空一个字符
            }
        }
        s1.push(str[i]);//继续入栈
    }
    while(!s1.empty())
    {
        s2.push(s1.top());//将一个栈的元素运送到另一个栈中，假如录入第一个栈顺序为1，2，3
        //则进入另一个栈中的顺序为3，2，1
        //则最后输出顺序就为1，2，3（看上面的图理解一下）
        s1.pop();
    }
    while(!s2.empty())
    {
        printf("%c",s2.top());
        s2.pop();//”倒着"出栈
    }
    printf("\n");
    return 0;
}

2.括号匹配
假设表达式中允许包含圆括号和方括号两种括号，其嵌套的顺序随意，如（［］（））或［（［］［］）］等为正确的匹配，［（］）或（［］（）或（（）））均为错误的匹配。
本题的任务是检验一个给定表达式中的括号是否正确匹配。
输入一个只包含圆括号和方括号的字符串，判断字符串中的括号是否匹配，匹配就输出“OK”，不匹配就输出“Wrong”。
Input
一行字符，只含有圆括号和方括号，个数小于 255。
Output
匹配就输出一行文本“OK”，不匹配就输出一行文本“Wrong”。
Sample Input
[(])
Sample Output
Wrong

#include
using namespace std;
typedef long long ll;
char s[300];
int main()
{
  scanf("%s",s);
    int l=strlen(s);
    stack<char>q;//初始化栈
    char tmp;
    for(int i=0; i<l; i++)
    {
        if(q.empty())
        {
            q.push(s[i]);//入栈
        }
        else
        {
            tmp=q.top();//赋值栈顶
            if((tmp=='['&&s[i]==']')||(tmp=='('&&s[i]==')'))//准确理解题意，
            {
                q.pop();//出栈
            }
            else
            {
                q.push(s[i]);//入栈
            }
        }
    }
    if(q.empty())//栈的输出
    {
        printf("OK\n");
    }
    else
    {
        printf("Wrong\n");
    }
    return 0;
}

3.加法与乘法
给定一个只包含加法和乘法的算术表达式，请编程计算表达式的值。
Input
输入仅有一行，为需要计算的表达式。表达式中只包含数字、加法运算符“+”和乘法运算符“*”，且没有括号，所有参与运算的数字均为 0~2^31 -1 之间的整数。输入数据保证这一行只有0~9、+、* 这 12 种字符。
Output
输出只有一行，包含一个整数，表示这个表达式的值。注意：当答案长度多于 4 位时，请只输出最后 4 位，前导 0 不输出。
Sample Input
【输入样例 1】
1+13+4
【输出样例 1】
8
【输入样例 2】
1+12345678901
【输出样例 2】
7891
【输入样例 3】
1+1000000003*1
【输出样例 3】
4

Sample Output

–

#include 
#include 
#include 
using namespace std;//此题不讲解，自悟
stack<int>s;
int flag;
void f()//定义一个函数
{
     int xx;
     char chch;
     int tmptmp=s.top();
            s.pop();
            scanf("%d",&xx);
            s.push(((tmptmp%10000)*(xx%10000))%10000);//如果多于4位只输出后四位
            scanf("%c",&chch);
            if(chch=='*') 
            f();          
            if(chch=='\n')
             {flag=1;}
}
int main()
{
    int x,ans=0;
    char ch;
    while(1)
    {
        scanf("%d",&x);
        s.push(x);//入栈
        scanf("%c",&ch);
        if(ch=='+')
         continue;
        if(ch=='*')
        f();
        if(ch=='\n'||flag==1)
        {break;}
    }
    while(!s.empty())
    {
    ans=(s.top()%10000+ans)%10000;
    s.pop();
    }
    cout<<ans<<endl;
    return 0;
}

**

往期回顾

**
原文链接：二分法
1.乱序排序
有n(1<=n<=2000005)个整数，是乱序的，现在另外给一个整数x，请找出序列排序后的第1个大于x的数的下标！
Input
输入数据包含多个测试实例，每组数据由两行组成，第一行是n和x，第二行是已经有序的n个整数的数列。
Output
对于每个测试实例，请找出从小到大排序后的序列中第1个大于x的数的下标！。
Sample Input
3 3
1 4 2
Sample Output
2

#include 
#include //超级简单的一道题
#include 
#include 
using namespace std;
const int N=2E6+9;
int a[N];
int main()
{
    int n,x,ans;
    while(~scanf("%d%d",&n,&x))
    {
        for(int i=1; i<=n; i++)
        {
            scanf("%d",&a[i]);
        }
        sort(a,a+n);
       int ans=upper_bound(a,a+n,x)-a;
        cout <<ans<< endl;
    }
    return 0;
}

2.分段
对于给定的一个长度为N的正整数数列A-i，现要将其分成M(M≤N)段，并要求每段连续，且每段和的最大值最小。
关于最大值最小：
例如一数列4 2 4 5 1要分成3段
将其如下分段：

[4 2][4 5][1]

第一段和为6，第2段和为9，第3段和为1，和最大值为9。

将其如下分段：

[4][2 4][5 1]

第一段和为4，第22段和为6，第33段和为6，和最大值为6。
并且无论如何分段，最大值不会小于6。
所以可以得到要将数列4 2 4 5 1要分成3段，每段和的最大值最小为6。
Input
第11行包含两个正整数N，M。
第22行包含N个空格隔开的非负整数A_i
含义如题目所述。
Output
一个正整数，即每段和最大值最小为多少。
Sample Input
5 3
4 2 4 5 1
Sample Output
6
Hint
N≤100000,M≤N,A i之和小于1e9

本题最大值的最小化
注意  l=max(a[i]),r=sum(a[i]),这是必须的，例如：
5 3
1 2 5 888888 4
会发现当mid=3时，888888和4 都没起作用，和题意不符；
见代码：
#include 
using namespace std;
const int N=1e5+5;
int a[N];
int n,k;
int check(int x)
{
    int num=1,sum=0;//这里感谢齐芒的提醒，num=1和num=0的感兴趣的可以试试
    for(int i=1;i<=n;i++)
    {
        sum+=a[i];
        if (sum>x)
        {
            num++;
            sum=a[i];
        }
    }
    if (num>k) return 1;
    else return 0;
}

int check1(int x)
{
    int num=1,sum=0;
    for(int i=1;i<=n;i++)
    {
        sum+=a[i];
        if (sum>x)
        {
            num++;
            sum=a[i];
        }
    }
    return num;
}
int main()
{
    //ios::sync_with_stdio(false);
    int len=0,mid,ma=0;
    cin>>n>>k;
    for(int i=1;i<=n;i++)
        {
        cin>>a[i];
        len+=a[i];
        ma=max(ma,a[i]);
        }
    int l,r;
    l=ma;r=len;//这里很重要，l必须要等于max(a[i])
    while(l<=r)
    {
        mid=(l+r)/2.0;
        if (check(mid)==1)
            l=mid+1;
        else
            r=mid-1;
    }
    cout<<l<<endl;
    return 0;
}

本期练习

1.溶液配制
小蓝虽然有很多溶液，但是还是没有办法配成想要的溶液，因为万一倒错了就没有办法挽回了。因此，小蓝到网上下载了一个溶液配置模拟器。模拟器在计算机中构造一种虚拟溶液，然后可以虚拟地向当前虚拟溶液中加入一定浓度、一定体积的这种溶液，模拟器会快速地算出倒入后虚拟溶液的浓度和体积。当然，如果倒错了可以撤销。
模拟器的使用步骤如下：
1）为模拟器设置一个初始体积和浓度 V0、C0%。
2）进行一系列操作，模拟器支持两种操作：
P(v,c)操作：表示向当前的虚拟溶液中加入体积为 v 浓度为 c 的溶液；
Z 操作：撤销上一步的 P 操作。
Input
第一行两个整数，表示 V0 和 C0，0≤C0≤100；
第二行一个整数 n，表示操作数，n≤10000；
接下来 n 行，每行一条操作，格式为：P_v_c 或 Z。
其中 _ 代表一个空格，当只剩初始溶液的时候，再撤销就没有用了，这时只输出初始的体积和浓度。
任意时刻质量不会超过 2^31 -1。
Output
n 行，每行两个数 Vi，Ci，其中 Vi 为整数，Ci 为实数（保留 5 位小数）。
其中，第 i 行表示第 i 次操作以后的溶液体积和浓度。
Sample Input
100 100
2
P 100 0
Z
Sample Output
200 50.00000
100 100.00000
Hint
例子输入2：
100 100
2
Z
P 100 0
例子输出2：
100 100.00000
200 50.00000
下节提示
acm新手小白必看系列之（10）——队列精讲及例题