图卷积浅谈 Graph Convolution

图卷积浅谈 Graph Convolution

1.图数据

欧氏空间包含了欧氏几何和非欧几何两种。传统的数据类型，如1维数据（声纹、语音）、2维数据（图像）、三维数据（视频）都是欧式空间上的数据，而图数据和流形数据都是非欧式空间上的数据。
图数据是一种非常重要的数据类型，图是由节点和边组成的，图可以分为有向图和无向图。常见的图结构的数据有：社交网络、引文网络、分子结构等。通过对图数据的研究，可以应用到社交网络、引文网络中节点类型的预测、电商中的推荐系统、生物和化学中对分子结构的预测等。

2.为什么需要使用图卷积

在传统的数据中，如图像，图像是一种网格数据，有标准的形状，在进行卷积操作时，取出固定大小的patch，使用固定大小的卷积核进行卷积操作。而对于图数据来说，每个节点的邻节点数量都是不相同的，因此很难做到使用一个固定大小的卷积核进行卷积，因此传统的卷积方法在图数据上就无法应用。随着图数据的应用越来越多，因此人们开始寻求对图数据的卷积操作。

3.基于频谱域的图卷积

思想：把空间域上的图映射到谱域上进行卷积。
背景知识：傅里叶变换
首先构建一个拉普拉斯矩阵L=D-A
D：顶点度矩阵，对角矩阵
A：邻接矩阵，对称矩阵
拉普拉斯矩阵是半正定对称矩阵（半正定矩阵本身就是对称矩阵），有如下三个性质：
（1）对称矩阵一定n个线性无关的特征向量
（2）半正定矩阵的特征值一定非负
（3）对阵矩阵的特征向量相互正交，即所有特征向量构成的矩阵为正交矩阵。

拉普拉斯矩阵分解：

$L=U\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_n\end{array}\right)U^{-1}$

$U=\left(u_1,u_2,\cdots ,u_n\right)$是特征向量矩阵，且$U$是一个正交矩阵，$U{U}^T=E$

$\Lambda =\left(\begin{array}{cccc}{\lambda }_1& & & \\ & \ddots & & \\ & & & {\lambda }_n\end{array}\right)$是特征值矩阵，$u_l$是特征值${\lambda }_l$所对应的特征向量。

傅里叶变化

传统的傅里叶变化，$F(\omega )=\mathcal{F}[f(t)]=\int f(t)e^{-i\omega t}dt$，
$e^{-i\omega t}$即为基函数，其中$\omega$表示基函数的不同频率。基函数与$f(t)$积分，即可得到傅里叶变换之后的结果。
而在拉普拉斯矩阵中，我们使用特征向量$u_i$表示不同的基函数，而$\omega$所对应的的就是特征值${\lambda }_i$
在图上进行傅里叶变化：
$F\left({\lambda }_l\right)=\hat{f}\left({\lambda }_l\right)={\sum }_{i=1}^{N}f(i)u_l^{\ast }(i)$，其中$f(i)$是与图的顶点一一对应的，$u_l(i)$是第$l$个特征向量的第$i$个分量，那么类比于传统的傅里叶变化中的积分，在图上的傅里叶变化就相当于是特征值（频率） ${\lambda }_l$下的， $f$与 ${\lambda }_l$ 对应的特征向量 $u_l$ 进行内积运算。$u_l^{\ast }(i)$是特征向量 $u_l$ 的共轭向量。

表示成矩阵的形式：

$\left(\begin{array}{c}\hat{f}\left({\lambda }_1\right)\\ \hat{f}\left({\lambda }_2\right)\\ ⋮\\ \hat{f}\left({\lambda }_N\right)\end{array}\right)=\left(\begin{array}{cccc}{u}_1(1)& u_1(2)& \dots & u_1(N)\\ u_2(1)& u_2(2)& \dots & u_2(N)\\ ⋮& ⋮& \ddots & ⋮\\ u_N(1)& u_N(2)& \dots & u_N(N)\end{array}\right)\left(\begin{array}{c}f(1)\\ f(2)\\ ⋮\\ f(N)\end{array}\right)$

即：$\hat{f}=U^{T}f$

逆傅里叶变换

传统的傅里叶变换是对频率 $\omega$ 求积分：
${\mathcal{F}}^{-1}[F(\omega )]=\frac{1}{2\Pi }\int F(\omega )e^{i\omega t}d\omega$
在图上进行逆傅里叶变化，则是对${\lambda }_l$积分：
$f(i)={\sum }_{l=1}^N\hat{f}\left({\lambda }_l\right)u_l(i)$
用矩阵的形式进行表示：
$\left(\begin{array}{c}f(1)\\ f(2)\\ ⋮\\ f(N)\end{array}\right)=\left(\begin{array}{cccc}{u}_1(1)& u_2(1)& \dots & u_N(1)\\ u_1(2)& u_1(2)& \dots & u_N(2)\\ ⋮& ⋮& \ddots & ⋮\\ u_1(N)& u_2(N)& \dots & u_N(N)\end{array}\right)\left(\begin{array}{c}\hat{f}\left({\lambda }_1\right)\\ \hat{f}\left({\lambda }_2\right)\\ ⋮\\ \hat{f}\left({\lambda }_N\right)\end{array}\right)$
即：$f=U\hat{f}$

(1)spectral CNN方法

思想：把待卷积函数和卷积核通过傅里叶变换同时映射到谱域，在谱域上进行卷积操作，再把卷积的结果逆傅里叶变换，得到在空间域上的结果。
具体步骤如下：
给定待卷积函数$f$,卷积核$h$(随机初始化的参数矩阵，需要进行训练）
对待卷积函数进行傅里叶变化，得到 $\hat{f}=U^{T}f$
对卷积核进行傅里叶变化，得到$\hat{h}\left({\lambda }_l\right)={\sum }_{i=1}^{N}h(i)u_l^{\ast }(i)$=$\left(\begin{array}{cccc}\hat{h}\left({\lambda }_1\right)& & & \\ & \ddots & & \\ & & \hat{h}\left({\lambda }_n\right)& \end{array}\right)$
两者的卷积操作为：
$\left(\begin{array}{ccc}\hat{h}\left({\lambda }_1\right)& & \\ & \ddots & \\ & & \hat{h}\left({\lambda }_n\right)\end{array}\right)U^{T}f$
再对上面的结果进行逆傅里叶变化，得到：
$(f\ast h{)}_G=U\left(\begin{array}{ccc}\hat{h}\left({\lambda }_1\right)& & \\ & \ddots & \\ & & \hat{h}\left({\lambda }_n\right)\end{array}\right)U^{T}f$

可以简写成：$(f\ast h{)}_G=U\left(\left(U^{T}h\right)\odot \left(U^{T}f\right)\right)$，$\odot$表示内积运算

(2)ChebNet 切比雪夫图卷积网络

思想：在spectral CNN方法中，参数是全局的，需要n个参数，同时拉普拉斯矩阵分解计算量大。
在本方法中，对spectral CNN进行了改进，使用的是局部k个参数。
具体步骤：
在Chebyshev-CNN中，使用下面的方式定义了一个卷积核：
对于卷积核$\left(\begin{array}{cccc}\hat{h}\left({\lambda }_1\right)& & & \\ & \ddots & & \\ & & \hat{h}\left({\lambda }_n\right)& \end{array}\right)$中的每一个元素：

由原来的$\hat{h}\left({\lambda }_l\right)={\sum }_{i=1}^{N}h(i)u_l^{\ast }(i)$变成了$\hat{h}\left({\lambda }_l\right)={\sum }_{k=0}^{K-1}{\theta }_k{\lambda }_l^k$，参数个数由n
个变成了k个。

卷积核的矩阵形式表示为$g_{\theta }(\Lambda )={\sum }_{k=0}^{K-1}{\theta }_k{\Lambda }^k$, ${\theta }_k$是参数
更进一步的，利用切比雪夫多项式进行近似计算：

$g_{\theta }(\Lambda )={\sum }_{k=0}^{K-1}{\theta }_k{T}_k(\tilde{\Lambda })$，其中

切比雪夫多项式$T_k(\tilde{\Lambda })$定义为：$T_0=1$，$T_1=x$，$T_k(x)=2x{T}_{k-1}(x)-T_{k-2}(x)$，
$\tilde{\Lambda }=2\Lambda /{\lambda }_{\max }-I_n$，这一步的目的是把特征值都归一化到$(-1,1)$之间。

卷积操作：
$(x\ast g_{\theta })=\left(\begin{array}{ccc}{\sum }_{k=0}^{K-1}{\theta }_k{\lambda }_l^k& & \\ & \ddots & \\ & & {\sum }_{k=0}^{K-1}{\theta }_k{\lambda }_l^k\end{array}\right)x$

在该方法中，通过切比雪夫多项式近似计算，而避免了对拉普拉斯矩阵的分解，减少了计算量，同时参数个数也减少到了k个。
注：一般K取值为1或2，分别表示一阶邻域和二阶邻域。

(3)GCN（Graph Convolutional Network）

思想：该方法是对ChebNet方法的进一步近似，令 $k=1$，${\lambda }_{max}=2$

具体步骤：
在上面的方法中，我们已知卷积操作$g_{\theta }\star x\approx {\sum }_{k=0}^K{\theta }_k{T}_k(\tilde{\Lambda })x$
$\tilde{\Lambda }=2\Lambda /{\lambda }_{\max }-I_n$
更进一步地，我们令 $k=1$,得到

$g_{\theta }\star x\approx {\sum }_{k=0}^{K=1}{\theta }_k{T}_k(\tilde{\Lambda })x={\theta }_0{T}_0(\tilde{\Lambda })x+{\theta }_1{T}_1(\tilde{\Lambda })x$

又因为$T_0=1$，$T_1=x$，因此上式$={\theta }_{0}x+{\theta }_1\tilde{\Lambda }x$

令${\lambda }_{max}=2$，则 $\tilde{\Lambda }=2\Lambda /{\lambda }_{\max }-I_n=\Lambda -I_n$

因此上式$={\theta }_{0}x+{\theta }_1(\Lambda -I_n)x={\theta }_{0}x-{\theta }_1{D}^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}x$

为了避免过拟合，我们减少参数的数量，令$\theta ={\theta }_0=-{\theta }_1$

则可以得到$g_{\theta }\star x\approx \theta \left(I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\right)x$

因为$I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$是$(0,2)$之间的，为了防止梯度消失和梯度爆炸，我们进行重归一化：

$I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\to {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$，其中$\tilde{A}=A+I_N$，${\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$

(4)总结

基于频谱域的图卷积方法，都需要对整张图进行计算，受内存等条件的限制，难以在大规模的图上进行运算。

4.基于空间域的图卷积

在空间域上进行图卷积的思想：聚合中心节点和邻居节点的特征，然后为中心节点得到一个新的特征表达。

(1) PATCHY-SAN方法

思想：在图上进行卷积操作时，最大的限制就是每个节点的邻节点个数不同，无法使用一个固定大小的卷积核进行卷积，PATCHY-SAN方法是参考CNN对输入的图像进行局部关联的区域进行操作，因此也抽取图中的局部关联区域进行相应的操作，集体来说就是把一整张图切分成多个子图，每个子图的邻节点数量相同，然后使用一个固定大小的卷积核进行卷积操作。
具体步骤：
（1） 从图中选择一个固定长度的节点序列
先通过一个算法（如中心性测量方式），确定节点的排序，从该序列中根据一定的间隔S，选出w个节点构成最终的节点序列
（2） 邻居节点收集
对于上一步获得的节点序列中的每一个节点，利用广度优先搜索扩展邻居节点，和源节点一起构成一个至少k大小的邻域集合。
（3） 图规范化
对邻域集合中的各个节点标号排序，得到k维的接受域（即邻域，给每个中心节点选择k个邻节点），如果第一步中不足w个节点，则直接在这一步中，把接受域都置为全0，相当于padding的作用。
（4） 卷积结构
对于节点属性，k个节点的属性值构成了一个输入通道，对于边的属性，k*k个属性值构成了另一个输入通道。
总结：该方法的关键步骤有两个，一个是如何对节点进行排序，二是如何给选定的w个节点构建接受域。该方法的缺点：把每个节点的邻节点强行约束为k个，会导致后续的预测效果降低。

(2) GraphSage 归纳学习图卷积

源论文：Inductive Representation Learning on Large Graphs
归纳学习和直推式学习：
数据集：标签数据+为标签数据+测试数据
直推式学习：在学习过程中，对所有的数据进行学习，然后对没标记数据进行预测，预测的节点是网络已见节点。直推式学习只能学习一张图上的数据，不能泛化到其他图中。
归纳学习：在学习过程中，测试数据不参与学习，然后对测试数据进行预测，即预测的节点是网络未见节点。归纳学习，可以将学习到的模型泛化到其他图上。

算法思想：每个节点都聚合它的k阶邻域的邻居节点的表示，映射到一个新的空间上，从而得到一个新的表示方法，这个表示方法在它的映射空间中有这样的一些性质：原来关系紧密的节点，在映射空间中，它们的距离更近，原来关系不紧密的节点，在映射空间中，它们的距离更远。

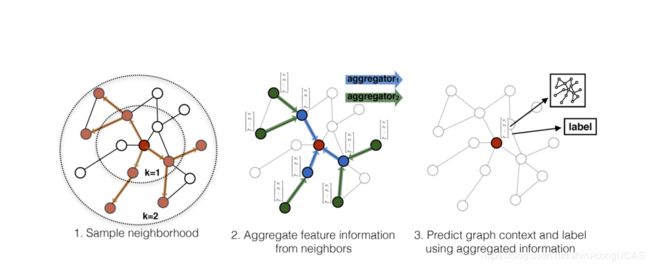
算法描述：
输入：图$\mathcal{G}(\mathcal{V},\mathcal{E})$，每个节点的特征向量$\left\{{\mathbf{x}}_v,\forall v\in \mathcal{V}\right\}$，给定$K$的值，当$K=1$时表示一阶邻域，当$K=2$时表示二阶邻域。

（1）首先聚合其k=1阶邻域内所有节点的特征向量，给节点$v$初始化一个表示向量：${\mathbf{h}}_v^0\leftarrow {\mathbf{x}}_v,\forall v\in \mathcal{V}$
（2）聚合节点$v$一阶邻域内所有的邻居节点的表示：

${\mathbf{h}}_{\mathcal{N}(v)}^k\leftarrow$ AGGREGATE ${}_k\left(\left\{{\mathbf{h}}_u^{k-1},\forall u\in \mathcal{N}(v)\right\}\right)$

这里聚合的邻居节点，并不是其原始的特征表示形式${\mathbf{x}}_u$，而是其$k-1$阶聚合之后的表达形式${\mathbf{h}}_u^{k-1}$，同时这里的AGGREGATE表示的是聚合函数，之后详细介绍。
（3）把聚合的邻居节点$(k-1)$的特征表达和节点本身$(k-1)$阶的特征表达进行拼接，得到节点$v$的$k$阶表示：
${\mathbf{h}}_v^k\leftarrow \sigma \left({\mathbf{W}}^k\cdot \mathrm{CONCAT}\left({\mathbf{h}}_v^{k-1},{\mathbf{h}}_{\mathcal{N}(v)}^k\right)\right)$
进行归一化操作，得到：
${\mathbf{h}}_v^k\leftarrow {\mathbf{h}}_v^k/{\Vert {\mathbf{h}}_v^k\Vert }_2,\forall v\in \mathcal{V}$

（4）聚合完k=1时的所有节点之后，逐个聚合$k=2,3...K$,把最终$k=K$的聚合结果赋值给
${\mathbf{z}}_v\leftarrow {\mathbf{h}}_v^K,\forall v\in \mathcal{V}$
聚合函数：
（1）Mean aggregator：${\mathbf{h}}_v^k\leftarrow \sigma (\mathbf{W}\cdot \mathrm{MEAN}\left(\left\{{\mathbf{h}}_v^{k-1}\right\}\cup \left\{{\mathbf{h}}_u^{k-1},\forall u\in \mathcal{N}(v)\right\}\right)$

（2）LSTM aggregator：把所有的邻域表达向量通过一个LSTM网络，得到一个聚合的输出结果，因为聚合函数不受输入顺序的影响，因此在输入网络中，可以任意顺序输入。

（3）Pooling aggregator ：AGGREGATE ${}_k^{\text{ pool }}=\max \left(\left\{\sigma \left({\mathbf{W}}_{\text{ pool }}{\mathbf{h}}_{u_i}^k+\mathbf{b}\right),\forall u_i\in \mathcal{N}(v)\right\}\right)$
虽然文中提出了3中聚合方式，但通过实验证明，Max Pooling aggregator 的效果更好。
损失函数
对于聚合之后的结果，我们要进行参数训练，使用的损失函数为：

$J_{\mathcal{G}}\left({\mathbf{z}}_u\right)=-\log \left(\sigma \left({\mathbf{z}}_u^{\top }{\mathbf{z}}_v\right)\right)-Q\cdot {\mathbb{E}}_{v_n\sim P_n(v)}\log \left(\sigma \left(-{\mathbf{z}}_u^{\top }{\mathbf{z}}_{v_n}\right)\right)$

$u$和$v$是在一个固定长度的随机游走中，一同出现的节点,而$P_{n(v)}$表示不和$u$一同出现的节点。该损失函数如果越小，那么$\log \left(\sigma \left({\mathbf{z}}_u^{\top }{\mathbf{z}}_v\right)\right)$就要越大，${\mathbf{z}}_u^{\top }{\mathbf{z}}_v$就要越大，而${\mathbf{z}}_u^{\top }{\mathbf{z}}_v$表示的是余弦相似性，余弦相似性越大，那么两个向量在映射空间的距离越近。因为在随机游走的路线中一同出现，因此节点$u$和$v$比较相近，因此两者在映射空间的余弦相似性越大。反之，对于不在随机游走的路线中一同出现的节点$P_{n(v)}$，则希望他们的余弦相似性越小，最终当损失函数趋近于平衡时，那么图中相近的点会在空间中聚集，图中远的点，也会在映射空间中分离。

总结：该方法只是学习了节点的一种特征表达，需要在通过一些其他算法，对节点进行分类。同时这种归纳式的学习，可以泛化到其他的图中。

(2) 混合卷积模型MoNet

算法思想：构建了一个混合模型，可以同时应用于图像、图和流形中。
在图像上的卷积，即传统的CNN模型；在图上的卷积，GCN模型；在流形上的CNN，主要有两种模型，一个是Geodesic GCN，另一个是Anisotropic GCN。
具体算法：
卷积操作：
构建一个patch
$D_j(x)f={\sum }_{y\in \mathcal{N}(x)}{w}_j(\mathbf{u}(x,y))f(y),j=1,\dots ,J$

$J$表示抽取的patch的大小，

在Geodesic GCN和Anisotropic GCN中，都手工构建了一个固定大小的权重，在本方法中，使用了一个可以训练的参数${\mathbf{\Sigma }}_j\in R^{d\times d}$ 和 ${\mathbf{\mu }}_j\in R^{d\times 1}$，构建了一个可以被学习的权重$w_j(\mathbf{u})$，构建方法如下：

$w_j(\mathbf{u})=\exp \left(-\frac{1}{2}{\left(\mathbf{u}-{\mathbf{\mu }}_j\right)}^{\top }{\mathbf{\Sigma }}_j^{-1}\left(\mathbf{u}-{\mathbf{\mu }}_j\right)\right)$

最终卷积操作表示为：
$(f\star g)(x)={\sum }_{j=1}^J{g}_j{D}_j(x)f$

为了计算$w_j(\mathbf{u})$，需要先构建伪坐标$\mathbf{u}(x,y)$：

原始的CNN、GCNN、ACNN、GCN、DCN模型都相当于混合模型的一种特例，针对不同的模型，构建伪坐标的方式不同：
（1）针对CNN，混合模型把取出的一个patch，给每个像素点赋值一个坐标值，如下图所示，而伪坐标$\mathbf{u}(x,y)$

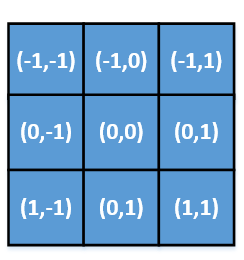
（2）针对GCNN和DCNN就是对测地极坐标，构建伪坐标
（3）针对GCN，就是针对节点的度，进行构建伪坐标，$\mathbf{u}(x,y)={\left(\frac{1}{\sqrt{\mathrm{deg}(\mathrm{x})}},\frac{1}{\sqrt{\mathrm{deg}(\mathrm{y})}}\right)}^{\top }$。

(3) GAT-Graph Attention Networks

思想：图attention是self-attention机制在图数据上的应用，通过自注意力机制学习节点$i$和邻节点$j$之间的一个权重系数${\alpha }_{ij}$，该系数表示的是节点$i$与节点$j$之间的重要性程度，最终节点$i$的特征表示就是邻节点的加权和。
具体步骤：
（1）学习权重${\alpha }_{ij}$
$e_{ij}=a\left(\mathbf{W}{h}_i,\mathbf{W}{h}_j\right)$，其中$h_i,h_j$表示的是节点$i$和节点$j$的特征向量（$h_i,h_j$$\in R^F$），$\mathbf{W}{h}_i,\mathbf{W}{h}_j$表示把原始的特征向量映射到另一个空间（$\mathbf{W}{h}_i,\mathbf{W}{h}_j\in {\mathbb{R}}^{F^{\prime }}$）。$a$表示的是自注意力函数，在本论文中采用的是
$e_{ij}$=LeakyReLU $\left({\mathbf{a}}^T\left[\mathbf{W}{h}_i\Vert \mathbf{W}{h}_j\right]\right)$，即先把$\left(\mathbf{W}{h}_i,\mathbf{W}{h}_j\right)$进行拼接操作，乘以一个权重矩阵${\mathbf{a}}^T$，再通过LeakyReLU激活函数得到$e_{ij}$
最后把$e_{ij}$归一化得到${\alpha }_{ij}$：

${\alpha }_{ij}={\mathrm{softmax}}_j\left(e_{ij}\right)=\frac{\exp \left(e_{ij}\right)}{{\sum }_{k\in {\mathcal{N}}_i}\exp \left(e_{ik}\right)}$（${\mathcal{N}}_i$表示节点i的邻节点）

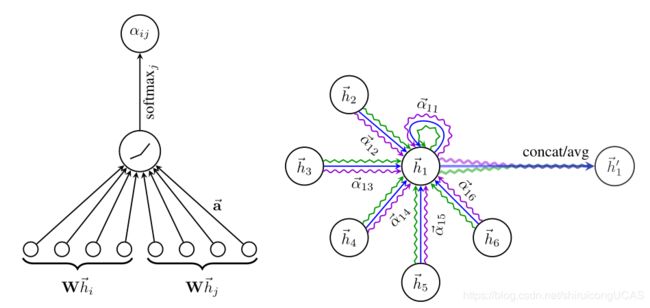
（2）构建节点i的特征表示$h_i^{\prime }$

$h_i^{\prime }=\sigma \left({\sum }_{j\in {\mathcal{N}}_i}{\alpha }_{ij}\mathbf{W}{h}_j\right)$
特别的，为了提高模型的稳定性，让模型有更好的表现，可以采取多头自注意力机制，设定K个自注意力机制，每个自注意力机制单独进行学习，最后把学习到的结果进行一个融合，融合的方式有以下两种：

$h_i^{\prime }={\Vert }_{k=1}^K\sigma \left({\sum }_{j\in {\mathcal{N}}_i}{\alpha }_{ij}^k{\mathbf{W}}^k{h}_j\right)$

$h_i^{\prime }=\sigma \left(\frac{1}{K}{\sum }_{k=1}^K{\sum }_{j\in {\mathcal{N}}_i}{\alpha }_{ij}^k{\mathbf{W}}^k{h}_j\right)$

总结：使用GAT模型时，可以在所有的边上和所有的节点上进行并行学习，所有的节点和所有的边都共享同一个自注意力机制。相比于之前的模型，GAT模型的容量更大，有更好的表现性能，最重要的是，GAT不用固定输入的大小，还可以连接所有的邻居节点。

(4) 总结

基于空间的图卷积，可以对图中的节点进行操作，而不用计算一整张图，因此随着节点数量的增加，基于谱域的卷积计算量就会快速增加，而基于空间域的方法，是对图中部分节点进行聚合计算的，因此计算量不会显著增加，因此基于空间域的卷积更适合在大规模的图上做计算，同时还可以使用mini-batch的方法进行训练。
基于谱域的图卷积，被限制只能对无向图进行卷积，而基于空间域的方法，能更灵活的处理有向图的问题。
基于谱域的图卷积，要求图有固定的大小，因此很难泛化到其他图中，而基于空间域的图卷积，可以很好的泛化到其他图上。