- 有向图强连通分量
- 1 基本概念
- 1.1 名词解释
- 1.2 重要性质
- 1.3 结论
- 2. 板子
- 3. 例题
- 3.1 tarjan + 缩点 + 度
- 3.2 tarjan + 缩点 + dp
- 3.2.1 求最长链、求方案数
- 3.2.2 求解差分约束
- 3.2.3 求解必经点问题
- 1 基本概念
有向图强连通分量
1 基本概念
1.1 名词解释
强连通分量:如果有向图中任意两点都有互相可达的路径,则此图为强连通图。有向图G的极大强连通子图称为G的强连通分量(SCC)(单点肯定都是scc,但要使scc尽可能大,所以能大尽量大)
dfn[x]数组:时间戳,记录每一个点被dfs访问到的顺序,某个点的dfs越小,表示该点越浅,dfs数组从1开始
low[x]:代表在dfs数中,此点以及其后代指出去的边,能返回到的最浅的点的时间戳
缩点: 可以将一个强连通分量当做一个超级点,而点权按题意来定。
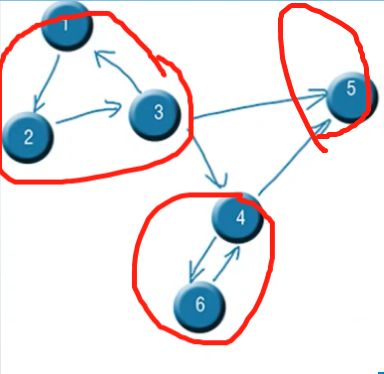
示例如下:缩点前=>缩点后

1.2 重要性质
scc性质:
(1).一个强连通分量内所有点的low[]值都相同
(2).一个强连通分量的根的low[root]==dfn[root]
(3).任何一个点的low[x]<=dfn[x]
缩点性质:
- 遍历每一个点,遍历每一个点的出边,如果出边的两个端点分别在两个scc[1]和scc[2]内,那么建立一条新的边add(scc[1],scc[2]),表示这两个scc间有一条有向边;
- 同时缩点后,缩点的下标与拓扑序反序,因此把sccnum从大到小(即拓扑顺序)就可以进行动态规划求出很多东西,比如说方案,最长链等。
1.3 结论
和度有关性质
- 缩点后,对于新图而言,只需要往入度为0的点注入水流,整张图就可以都有水
- 缩点后,对于新图而言,把一张dag变为一张scc只需要添加max(入度为0的点数目,出度为0的点数目)条边
- 一张图中其他所有点都可达的点就是出度为0的点,因此,只需要缩点,新图中出度为0的超级点内含的点数目就是答案。
- 注意:当统计出度/入度为k(k > 0)的时候需要判断重边
和dp有关的性质
- tarjan算法求出来的scc顺序是反拓扑序,因此可以利用这个性质做dp,即可用在tarjan算法的过程中做dp,也可由在tarjan算法进行完成后再做,且完成后做时间更优。
- 要求必须从起点开始,那么把起点当作tarjan算法的输入参数,求出来的所有缩点一定都是从起点开始的点
- 要求必须到达终点的情况,那么维护一个数组f2[i],f2[i]为1表示i能够到达终点,0表示不能到达终点。在tarjan求scc时,如果当前x点==n时,f[sccnum]=1
- 注意:当统计方案数的时候需要判重边
2. 板子
tarjan+缩点+拓扑序dp(反缩点顺序)
#include
using namespace std;
int const N = 1e5 + 10, M = 2e6 + 10;
// dfn记录每个点的时间戳,low记录每个点的回溯值,scc[i]=x表示i在标号为x的强连通分量里,stk维护一个栈,sccnum记录强连通分量的个数
int dfn[N], low[N], scc[N], stk[N], sccnum, top, timestamp;
int h1[N], e[M], ne[M], idx, h2[N];
int n, m, x;
int f[N], g[N];
int scc_count[N];
set exist; // 本题要求方案,因此需要对新图的边去重
// a->b有一条边
void add(int a, int b, int h[])
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// tarjan算法求强连通分量
void tarjan(int root, int h[])
{
if (dfn[root]) return; // 时间戳不为0,返回
dfn[root] = low[root] = ++timestamp; // 记录当前点的时间戳和回溯值,初始化二者相同,而后dfn[root]>=low[root]
stk[++top] = root; // 把根放入栈内
for (int i = h[root]; i != -1; i = ne[i]) // 遍历每一个与根节点相邻的点
{
int j = e[i]; // 与i相邻的点为j
if (!dfn[j]) // j点没有访问过
{
tarjan(j, h); // 继续dfs,得到所有以j点为根的子树内所有的low和dfn
low[root] = min(low[root], low[j]); // 根的low是其子树中low最小的那个
}
else if (!scc[j]) // 如果j这个点还在栈内(在栈内的话不属于任何一个scc),同时一个栈内的点在一个scc内
{
low[root] = min(low[root], dfn[j]); // low代表所能到达的最小的时间戳
}
}
// 如果root的后代不能找到更浅的节点(更小的时间戳)
if (low[root] == dfn[root]) // 只有某个强连通分量的根节点的low和dfn才会相同
{
sccnum++;
while (1) // 出栈直到等于root
{
int x = stk[top--];
scc[x] = sccnum;
if (x == root) break;
}
}
}
int main()
{
cin >> n >> m >> x;
memset(h1, -1, sizeof h1);
memset(h2, -1, sizeof h2);
for (int i = 1; i <= m; ++i)
{
int a, b;
scanf("%d %d", &a, &b);
add(a, b, h1);
}
// tarjan求scc
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i, h1);
// 计算每个强连通分量内点的个数
for (int i = 1; i <= n; ++i)
{
scc_count[scc[i]] ++;
}
// 缩点
for (int i = 1; i <= n; ++i)
{
for (int j = h1[i]; j != -1; j = ne[j])
{
int k = e[j];
if (scc[i] != scc[k] && !exist.count(scc[i] * 100000ll + scc[k])) // 本题要求方案,因此需要对新图的边去重,如果不求方案,则不需要去重
{
add(scc[i], scc[k], h2);
exist.insert(scc[i] * 100000ll + scc[k]);
}
}
}
// 按照缩点的逆序(拓扑序顺序)进行dp
for (int i = sccnum; i; --i)
{
if (!f[i]) // 初始化
{
f[i] = scc_count[i];
g[i] = 1;
}
for (int j = h2[i]; j != -1; j = ne[j])
{
int k = e[j];
if (f[k] < f[i] + scc_count[k])
{
f[k] = f[i] + scc_count[k];
g[k] = g[i];
}
else if (f[k] == f[i] + scc_count[k]) g[k] = (g[k] + g[i]) % x;
}
}
// 计算最大值
int maxi = 0, sum = 0;
for (int i = 1; i <= sccnum; ++i)
{
if (f[i] > maxi)
{
maxi = f[i];
sum = g[i];
}
else if (f[i] == maxi) sum = (sum + g[i]) % x;
}
cout << maxi << "\n" << sum << endl;
return 0;
}
3. 例题
3.1 tarjan + 缩点 + 度
P2341 受欢迎的牛
每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂,每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果 A喜欢 B,B喜欢 C,那么 A 也喜欢 C。牛栏里共有 N 头奶牛,给定一些奶牛之间的爱慕关系,请你算出有多少头奶牛可以当明星。
奶牛数目N~1e4, 传递关系M~5e4
/* 建图,缩点,建新图,然后统计新图是否是一个连通图,如果不是,那么答案为0;
如果新图是一个连通图,那么统计出度为0的点的数目,如果>=2,那么答案为0;
如果为1,那么为这个超级点内的点数目。 */
#include
using namespace std;
int const N = 1e4 + 10, M = 1e5 + 10;
// dfn记录每个点的时间戳,low记录每个点的回溯值,scc[i]=x表示i在标号为x的强连通分量里,stk维护一个栈,sccnum记录强连通分量的个数
int dfn[N], low[N], scc[N], stk[N], sccnum, top, timestamp;
int h1[N], e[M], ne[M], idx;
int n, m, x;
int scc_count[N], dout[N];
// a->b有一条边
void add(int a, int b, int h[])
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// tarjan算法求强连通分量
void tarjan(int root, int h[])
{
if (dfn[root]) return; // 时间戳为0,返回
dfn[root] = low[root] = ++timestamp; // 记录当前点的时间戳和回溯值,初始化二者相同,而后dfn[root]>=low[root]
stk[++top] = root; // 把根放入栈内
for (int i = h[root]; i != -1; i = ne[i]) // 遍历每一个与根节点相邻的点
{
int j = e[i]; // 与i相邻的点为j
if (!dfn[j]) // j点没有访问过
{
tarjan(j, h); // 继续dfs,得到所有以j点为根的子树内所有的low和dfn
low[root] = min(low[root], low[j]); // 根的low是其子树中low最小的那个
}
else if (!scc[j]) // 如果j这个点还在栈内(在栈内的话不属于任何一个scc),同时一个栈内的点在一个scc内
{
low[root] = min(low[root], dfn[j]); // low代表所能到达的最小的时间戳
}
}
// 如果root的后代不能找到更浅的节点(更小的时间戳)
if (low[root] == dfn[root]) // 只有某个强连通分量的根节点的low和dfn才会相同
{
sccnum++;
while (1) // 出栈直到等于root
{
int x = stk[top--];
scc[x] = sccnum;
if (x == root) break;
}
}
}
int main()
{
cin >> n >> m;
memset(h1, -1, sizeof h1);
for (int i = 1; i <= m; ++i)
{
int a, b;
scanf("%d %d", &a, &b);
add(a, b, h1);
}
// tarjan求scc
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i, h1);
// 计算每个强连通分量内点的个数
for (int i = 1; i <= n; ++i)
{
scc_count[scc[i]] ++;
}
// 缩点
for (int i = 1; i <= n; ++i)
{
for (int j = h1[i]; j != -1; j = ne[j])
{
int k = e[j];
if (scc[i] != scc[k]) dout[scc[i]]++;
}
}
int cnt = 0, res = 0, cow = -1;
for (int i = 1; i <= sccnum; ++i) if (!dout[i]) cnt++, cow = i;
printf("%d", (cnt >= 2? 0: scc_count[cow]));
return 0;
}
acwing367 学校网络
给定一个有向图:N个点,求:
1)至少要选几个顶点,才能做到从这些顶点出发,可以到达全部顶点
2)至少要加多少条边,才能使得从任何一个顶点出发,都能到达全部顶点
/*先缩点
第一问:只需要往入度为0的点放入,即可到达其他所有的点
第二问:max(入度为0的点的数目,出度为0的点数目)
注意要特判下缩点后只有一个scc的情况*/
#include
using namespace std;
int const N = 1e2 + 10, M = N * N;
// dfn记录每个点的时间戳,low记录每个点的回溯值,scc[i]=x表示i在标号为x的强连通分量里,stk维护一个栈,sccnum记录强连通分量的个数
int dfn[N], low[N], scc[N], stk[N], sccnum, top, timestamp;
int h1[N], e[M], ne[M], idx;
int n, m, dout[N], din[N];
// a->b有一条边
void add(int a, int b, int h[])
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// tarjan算法求强连通分量
void tarjan(int root, int h[])
{
if (dfn[root]) return; // 时间戳为0,返回
dfn[root] = low[root] = ++timestamp; // 记录当前点的时间戳和回溯值,初始化二者相同,而后dfn[root]>=low[root]
stk[++top] = root; // 把根放入栈内
for (int i = h[root]; i != -1; i = ne[i]) // 遍历每一个与根节点相邻的点
{
int j = e[i]; // 与i相邻的点为j
if (!dfn[j]) // j点没有访问过
{
tarjan(j, h); // 继续dfs,得到所有以j点为根的子树内所有的low和dfn
low[root] = min(low[root], low[j]); // 根的low是其子树中low最小的那个
}
else if (!scc[j]) // 如果j这个点还在栈内(在栈内的话不属于任何一个scc),同时一个栈内的点在一个scc内
{
low[root] = min(low[root], dfn[j]); // low代表所能到达的最小的时间戳
}
}
// 如果root的后代不能找到更浅的节点(更小的时间戳)
if (low[root] == dfn[root]) // 只有某个强连通分量的根节点的low和dfn才会相同
{
sccnum++;
while (1) // 出栈直到等于root
{
int x = stk[top--];
scc[x] = sccnum;
if (x == root) break;
}
}
}
int main()
{
cin >> n;
memset(h1, -1, sizeof h1);
for (int i = 1, t; i <= n; ++i) {
while (scanf("%d", &t) && t) add(i, t, h1);
}
// tarjan求scc
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i, h1);
// 缩点
for (int i = 1; i <= n; ++i)
{
for (int j = h1[i]; j != -1; j = ne[j])
{
int k = e[j];
if (scc[i] != scc[k]) dout[scc[i]]++, din[scc[k]]++;
}
}
int cnt1 = 0, cnt2 = 0;
for (int i = 1; i <= sccnum; ++i) {
if (!dout[i]) cnt1 ++;
if (!din[i]) cnt2 ++;
}
printf("%d\n%d\n", max(1, cnt2), (sccnum == 1? 0: max(cnt1, cnt2)));
return 0;
}
acwing401从u到v还是从v到u? acwing402杀人游戏 acwing1175 最大半连通子图 acwing1169糖果 acwing341最优贸易
给定一个 n 个点 m 条边的有向图,现在要求图中任意两点u和v,均可满足u能通往v或v能通往u,请你判断要求是否能够成立。
0/*
一张有向图的中任意两个点u和v,均可满足u能通往v或v能通往u,那么这个有向图缩点后的dag的拓扑序唯一
拓扑序唯一就是每次队列里的元素个数小于等于1
*/
#include
有N个人,其中一个杀手,其余都是平民。警察能够对每一个人进行查证,假如查证的对象是平民,他会告诉警察,他认识的所有人当中,谁是杀手,谁是平民。假如查证的对象是杀手, 杀手将会把警察干掉。每一个人都有可能是杀手,可看作他们是杀手的概率是相同的。问:根据最优的情况,保证警察自身安全并知道谁是杀手的概率最大是多少?
1≤N≤105,0≤M≤3∗105/*
分析可知,缩点后,每次从入度为0的点开始搜索,那么可能死亡的概率最小,且只有从链头开始搜索的时候发生
因此,警察死的概率为 入度为0的点数目/总点数
需要特判一种情况
*/
#include3.2 tarjan + 缩点 + dp
3.2.1 求最长链、求方案数
求最大半连通子图的节点数以及方案数。
最大半连通子图:对于G的子图,如果u,v满足u->v或v->u的关系,且这个子图最大,那么就是最大半连通子图。
节点数N~1e5, 边数M~1e6/* 最大半连通子图就是最长链,即求最长链的长度及方案
本题缩点完求最长链的长度和方案,因此缩点完dp处理即可,f[i]表示到i点的最长链的长度,g[i]表示到i点的最长链的方案
由于缩点完之后点的下标就是按拓扑序的逆序的,因此可以按照逆序进行dp处理
处理的方法参加背包问题求方案数 */
#include3.2.2 求解差分约束
幼儿园里有 N 个小朋友,老师现在想要给这些小朋友们分配糖果,要求每个小朋友都要分到糖果。老师需要满足小朋友们的 K 个要求。老师想知道他至少需要准备多少个糖果。
要求有5种:
如果 X=1.表示第 A 个小朋友分到的糖果必须和第 B 个小朋友分到的糖果一样多。
如果 X=2,表示第 A 个小朋友分到的糖果必须少于第 B 个小朋友分到的糖果。
如果 X=3,表示第 A 个小朋友分到的糖果必须不少于第 B 个小朋友分到的糖果。
如果 X=4,表示第 A 个小朋友分到的糖果必须多于第 B 个小朋友分到的糖果。
如果 X=5,表示第 A 个小朋友分到的糖果必须不多于第 B 个小朋友分到的糖果。
N~1e5, K~1e5, 1 <=A, B <= N/*
原来的思路是建图后,做差分约束,跑spfa,一旦发现出现正环那么无解,否则求出最长距离,然后累加,这种方法时间卡在spfa上,
spfa有可能跑出O(nm)的时间导致超时
由于数据比较特殊,只有0和1两种,那么可以换一个方法:
对于每一个环,它一定是属于scc,而只要出现1条边权为1的边那么就是出现正环,所有我们可以缩点后,判断每个scc内部是否出现
边权为1的边,一旦出现就是正环,无解;如果没有出现,那么有解,求完scc后缩点,然后按照缩点的逆序(拓扑序)进行dp,求出
最长链dis,然后答案就是每个超级点内点的个数*这个点的最长距离的累加值。
*/
#include3.2.3 求解必经点问题
给出 n个城市的水晶球价格,m 条道路的信息。在1->N路径(可以不简单)上买1次卖1次,最多能赚多少钱。/*
本题要找1 ~ n上最大的点和最小的点
考虑dp求解,维护数组f1[i]表示i点开始到n点的最大价值,然后去枚举i为买的点,答案即为max{val[i]-f1[i]}
但是本题可能存在环,因此考虑tarjan算法缩点变成dag
本题的难点在于要求当前的点i必须是从1开始,到n结束
从1开始好处理,tarjan算法的时候只做1为起点的tarjan,这样求出来的都是从1开始的
而到n结束就必须维护一个数组f2[i]表示i是否能够到n点,f2[i]为1表示i能够到n点,为0表示不能到n点,每次都必须更新f2
维护数组f1[i]表示i点开始到n点的最大价值,当且仅当f2[i]=1才能转移,f1[i]=max[max{f1[u]}, val[i]]
*/
#include