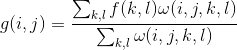常见的图像滤波算法

本文介绍五种常见的图像滤波方式：线性滤波（方框滤波、均值滤波、高斯滤波）；非线性滤波（中值滤波、双边滤波）。提醒，本文主要是算法公式，没有具体完整的代码。

 

一、线性滤波

总的来说，这三种线性滤波原理：每个像素的输出值是输入像素的加权和。其处理方式都是将图像像素与相应的核进行卷积，核即是权重（下图中中间3*3大小的图就是核），其作用是将原图像素按权重进行分配。简单讲，卷积就是选取原图像与核相同大小的部分（下图左侧对照部分），然后与核对应相乘相加，所得的值赋给原图中的锚点（下图是中心点，右侧对照部分）（有关卷积的讲解可参考下图的转载链接）。

​

卷积（图像转自https://blog.csdn.net/zouxy09/article/details/49080029，侵删）

所以说，这三种滤波方式的区别在于卷积核的不同，下面分别叙述。

 

1.1方框滤波和均值滤波的卷积核

如下图，K即为方框滤波的核，可以看到无论a为何值，矩阵内的每一个元素都相等，卷积时对像素的权重都一样。均值滤波是方框滤波归一化后的特殊处理，下图中，当normalize = ture时的K为均值滤波的核。个人觉得，方框滤波和均值滤波没有实质上的区别。

​

 

1.2高斯滤波的卷积核

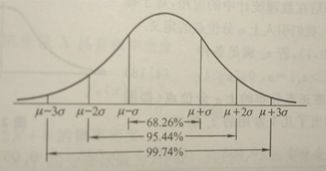
我们先来看一下一维高斯函数，如下图，a代表尖峰高度，b代表尖峰中心的x坐标，c是标准方差，代表尖峰的宽度。图3表示“3σ”原则，意思是，虽然定义域的范围是正无穷到负无穷，但是曲线的绝大部分都在“-3σ - 3σ”之间。

     ​   ​​

                         一维高斯函数（图1、2转载自https://blog.csdn.net/jorg_zhao/article/details/52687448，侵删）

接下来我们看看二维高斯函数，其服从当ρ=0时的二维正态分布，即x、y不相关。同样，参照一维高斯函数，A是幅值，即高度；x。y。是中心点坐标；σx σy是方差，代表底面的两个方向上的宽度。

          ​     ​

                       二维高斯函数（转载自https://blog.csdn.net/jorg_zhao/article/details/52687448，侵删）

在计算高斯核时，由于在x、y两个方向上我们所需要的宽度是完全一致的，所以我们可以取σx = σy，这时公式变为

                                                         

由上述公式，我们就可以求出高斯核，代码如下

//******************高斯卷积核生成函数*************************
//第一个参数Guass是存高斯卷积核的二维数组
//第二个参数size是高斯卷积核的尺寸大小；
//第三个参数sigma是卷积核的标准差
//*************************************************************
void CDisplay::GetGaussianKernel(double **Guass, const int size, const double sigma)
{
    const double PI = 4.0*atan(1.0); //圆周率π赋值
    int center = size / 2;
    double sum = 0;
    for (int i = 0; i)
    {
        for (int j = 0; j)
        {
            Guass[i][j] = (1 / (2 * PI*sigma*sigma))*exp(-((i - center)*(i - center) + (j - center)*(j - center)) / (2 * sigma*sigma));
            sum += Guass[i][j];
        }
    }
    for (int i = 0; i//归一化
    {
        for (int j = 0; j)
        {
            Guass[i][j] /= sum;
        }
    }
}

sigma与size值的选取：一般其情况，size = sigma*3+1，因为“3σ”原则。

 

二、非线性滤波

2.1中值滤波

基本思想：用像素点邻域灰度值的中值来代替该像素点的灰度值。

如下图，将中心点周围被称为邻域的像素点（包括自身）进行排序，取排序后9个像素值中间值作为当前新的像素值。

​

                    中值滤波原理图（图片转载自https://blog.csdn.net/qq_36359022/article/details/80116137，侵删）

 

 2.2双边滤波

基于空间分布的高斯滤波函数，其核为一个与空间距离相关的高斯函数与一个灰度距离相关的高斯函数相乘所得。简单说就是高斯滤波的加强版，在高斯滤波中，只有关于空间距离的权重，离中心点越远，权重越小，而双边滤波在此基础上添加了关于灰度距离的权重，邻域中的像素灰度值越接近中心点灰度值，权重越大。

下面开始来讲权重的计算获取。

空间距离：指的是当前点与中心点的欧式距离。空间域高斯函数其数学形式为：

                                                     

(i, j)代表输出点；(k, l)代表(多个)输入点；sigma为空间域标准差。

这也叫定义域核的表示形式，叫这个名字的原因，个人理解是：这里的权重只和平面位置距离有关，只和x、y有关。同时可以发现，这公式其实就是高斯滤波的公式。

灰度距离：指的是当前点灰度与中心点灰度的差的绝对值。值域高斯函数其数学形式为：

                                       

(i, j)代表输出点；(k, l)代表(多个)输入点；sigma为值域标准差。

同样，这也叫值域核的表示形式，理由和上面类似，其所求结果r只与灰度值有关。

将上述两公式相乘就可以得到，依赖数据的双边滤波权重函数：

                     

至此，即得到了双边滤波的权重，最后在将权重与像素对应相乘相加再除以权重和，即求出最后输出像素值。

                                             

再求出权重后，如果先归一化，最后这一步其实是在求卷积。个人认为，双边滤波的算法流程也是先求出一个核，只是这个核是在高斯核的基础上乘了一个代表灰度相似程度的一个权重，最后在进行类似卷积操作。

 

以上，便是部分了。本人小白一枚，有错还请指出，欢迎探讨。

转载于:https://www.cnblogs.com/wy1996/p/10858376.html