第三讲 Matlab/Simulink入门——离散系统仿真实例
第三讲 Matlab/Simulink入门——离散系统仿真实例
- 1、离散系统基本概念
- 1.1 离散系统
- 1.2线性离散系统
- 1.3 Z变换
- 2、人口变化(例1)仿真
- 2.1 人口变化模型
- 2.2 建模
- 2.3 系统仿真
- 3、低通滤波器(例2)仿真
- 3.1 低通滤波器模型
- 3.2 建模
- 3.3 系统仿真
1、离散系统基本概念
1.1 离散系统
离散系统: 是指系统的输入和输出仅在离散的时间上取值,而且离散的时间具有相同的时间间隔,与连续的概念相反。
设系统输入变量为 u ( n T s ) , n = 0 , 1 , 2... u(nT_s),n=0,1,2... u(nTs),n=0,1,2...,其中 T s T_s Ts为系统的采样时间, n n n为采样时刻。由于 T s T_s Ts为一固定值,因此系统输入 u ( n T s ) u(nT_s) u(nTs),常简记为 u ( n ) u(n) u(n)。设输出系统为 y ( n T s ) y(nT_s) y(nTs),简记为 y ( n ) y(n) y(n)。于是,离散系统的数学表达为:
y ( n ) = f ( u ( n ) , u ( n − 1 ) , . . . ; y ( n − 1 ) , y ( n − 2 ) ) y(n)=f(u(n),u(n-1),...;y(n-1),y(n-2)) y(n)=f(u(n),u(n−1),...;y(n−1),y(n−2))
1.2线性离散系统
线性离散系统: 是离散系统的一种特殊形式,需要同时满足(1)、(2)两个条件,即
T { α u 1 ( n ) + β u 2 ( n ) } = α T { u 1 ( n ) } + β T { u 2 ( n ) } T\lbrace \alpha u_1(n)+\beta u_2(n) \rbrace = \alpha T\lbrace u_1(n) \rbrace + \beta T\lbrace u_2(n) \rbrace T{αu1(n)+βu2(n)}=αT{u1(n)}+βT{u2(n)}
(1)、齐次性: 对于离散系统 y ( n ) = T { u ( n ) } , n = 0 , 1 , 2... y(n)=T\lbrace u(n) \rbrace, n=0,1,2... y(n)=T{u(n)},n=0,1,2...,如果对任意的输入 u ( n ) u(n) u(n)与给定的常数 α \alpha α,下面的式子总成立:
T { α u ( n ) } = α T { u ( n ) } T\lbrace \alpha u(n) \rbrace = \alpha T\lbrace u(n) \rbrace T{αu(n)}=αT{u(n)}
则称系统满足齐次性。
(2)、叠加性: 对于系统对于输出 u 1 ( n ) u_1(n) u1(n)和 u 2 ( n ) u_2(n) u2(n),输出分别为 y 1 ( n ) y_1(n) y1(n) 和 y 2 ( n ) y_2(n) y2(n),总有下面的式子成立:
T { u 1 ( n ) + u 2 ( n ) } = T { u 1 ( n ) } + T { u 2 ( n ) } T\lbrace u_1(n)+u_2(n) \rbrace = T\lbrace u_1(n) \rbrace + T\lbrace u_2(n) \rbrace T{u1(n)+u2(n)}=T{u1(n)}+T{u2(n)}
则称系统满足叠加性。
对于线性离散系统,其一般数学描述为:
y ( n ) = f ( u ( n ) , u ( n − 1 ) , . . . ; y ( n − 1 ) , y ( n − 2 ) ) y(n)=f(u(n),u(n-1),...;y(n-1),y(n-2)) y(n)=f(u(n),u(n−1),...;y(n−1),y(n−2))
用差分方程描述为:
状态方程: x ( n + 1 ) = f ( x ( n ) , u ( n ) , n ) x(n+1)=f(x(n),u(n),n) x(n+1)=f(x(n),u(n),n)
输出方程: y ( n ) = g ( x ( n ) , u ( n ) , n ) y(n)=g(x(n),u(n),n) y(n)=g(x(n),u(n),n)
1.3 Z变换
Z Z Z变换: 对于一个离散信号 u ( n ) u(n) u(n),其 Z Z Z变换为 U ( z ) = ∑ k = − ∞ ∞ u ( k ) z − k U(z)=\displaystyle \sum_{k=-\infty}^{\infty}{u(k)z^{-k}} U(z)=k=−∞∑∞u(k)z−k。一般来说离散信号 u ( n ) u(n) u(n)的起始时间往往大于零,这时它的 Z Z Z变换为 U ( z ) = ∑ k = 0 ∞ u ( k ) z − k U(z)=\displaystyle \sum_{k=0}^{\infty}{u(k)z^{-k}} U(z)=k=0∑∞u(k)z−k,可简记为 U ( z ) = Z { u ( n ) } U(z)=Z \lbrace u(n) \rbrace U(z)=Z{u(n)}。由离散信号的 Z Z Z变换确定离散信号的过程为 Z Z Z变换的你变换,一般简记为 U ( z ) = Z − 1 { u ( n ) } U(z)=Z^{-1} \lbrace u(n) \rbrace U(z)=Z−1{u(n)}。
Z Z Z变换有以下两个重要性质:
(1)、线性关系: Z Z Z变换同时满足齐次性和叠加性,即:
Z { α u 1 ( n ) + β u 2 ( n ) } = α Z { u 1 ( n ) } + β Z { u 2 ( n ) } Z\lbrace \alpha u_1(n)+\beta u_2(n) \rbrace = \alpha Z\lbrace u_1(n) \rbrace + \beta Z\lbrace u_2(n) \rbrace Z{αu1(n)+βu2(n)}=αZ{u1(n)}+βZ{u2(n)}
(2)、设离散信号 u ( n ) u(n) u(n)的 Z Z Z变换为 U ( z ) U(z) U(z),则 u ( n − 1 ) u(n-1) u(n−1)的 Z Z Z变换为 z − 1 U ( z ) z^{-1}U(z) z−1U(z)。
2、人口变化(例1)仿真
2.1 人口变化模型
【例1】设某一年的人口总数为 p ( n ) p(n) p(n),其中 n n n表示年份,它与上一年的人口数目 p ( n − 1 ) p(n-1) p(n−1)、人口自然增长率 r r r、以及新增资源所能满足的个体数目 K K K之间的关系方程如下差分方程,即:
p ( n ) = r p ( n − 1 ) [ 1 − p ( n − 1 ) K ] p(n)=rp(n-1)[1-\frac{p(n-1)}{K}] p(n)=rp(n−1)[1−Kp(n−1)]
现设人口初值 p ( 0 ) p(0) p(0)=500000,人口自然增长率 r r r=1.07, K K K=2000000,建立人口动态变化的数学模型,分析人口数目的变化趋势。
2.2 建模
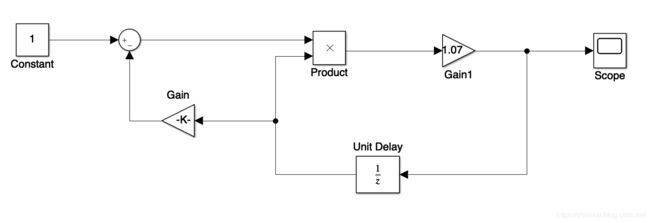
Gain模块:参数设置为1/2000000,即 1 K \frac{1}{K} K1。
Gain1模块:增益设为1.07,即人口自然增长率。
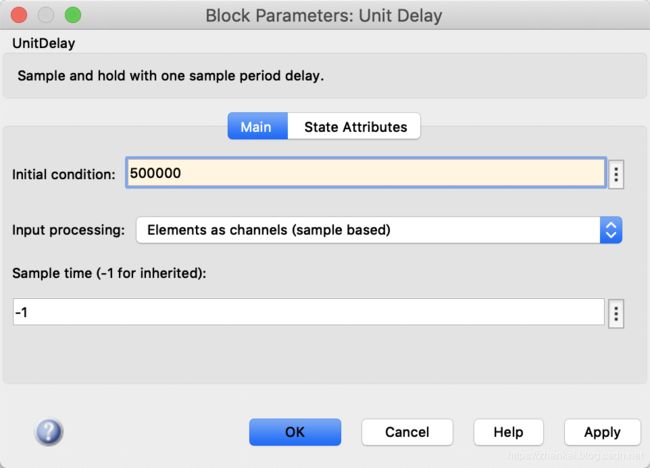
Unit Delay模块:参数设置如图所示。
Constant模块:常数1。
Sum模块:list of signs设置为| + -。

2.3 系统仿真
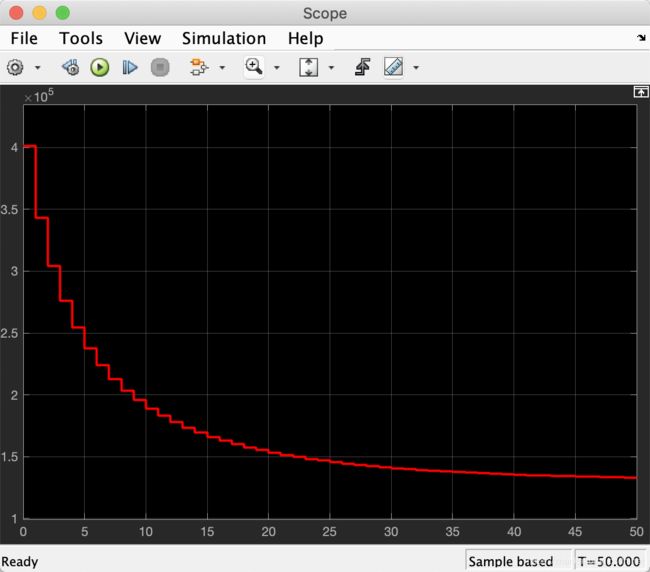
仿真时间设置为50s,步长默认(auto)也可以设置为其他。点击运行run,然后双击Scope模块,即可显示仿真结果。从仿真结果可以看出,人口数目会逐年减少,并趋于一个稳定值。
3、低通滤波器(例2)仿真
3.1 低通滤波器模型
【例2】低通滤波器可以过滤掉信号中的高频部分,以获取信号中有价值的低频信号。下面是一个低通数字滤波器的差分方程描述:
y ( n ) − 1.6 y ( n − 1 ) + 0.7 y ( n − 2 ) = 0.04 u ( n ) + 0.08 u ( n − 1 ) + 0.04 u ( n − 2 ) y(n)-1.6y(n-1)+0.7y(n-2)=0.04u(n)+0.08u(n-1)+0.04u(n-2) y(n)−1.6y(n−1)+0.7y(n−2)=0.04u(n)+0.08u(n−1)+0.04u(n−2)
其中, u ( n ) u(n) u(n)为滤波器输入,y(n)为滤波器输出。
对滤波器系统的差分方程进行 Z Z Z变换,即:
Y ( z ) U ( z ) = 0.04 + 0.08 z − 1 + 0.04 z − 2 1 − 1.6 z − 1 + 0.7 z − 2 \frac{Y(z)}{U(z)} = \frac{0.04+0.08z^{-1}+0.04z^{-2}}{1-1.6z^{-1}+0.7z^{-2}} U(z)Y(z)=1−1.6z−1+0.7z−20.04+0.08z−1+0.04z−2
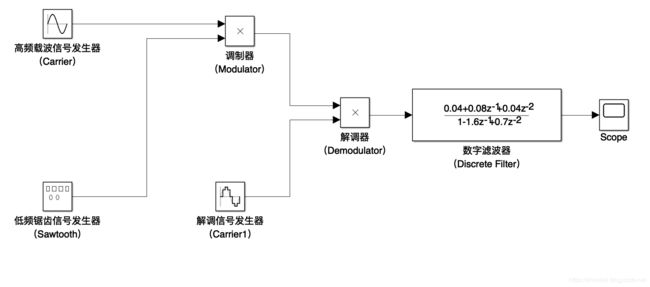
根据系统的数学描述进行建模。
3.2 建模
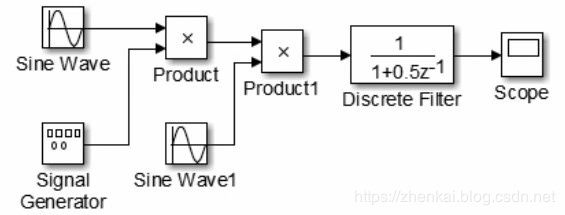
Sine Wave模块:Frequency频率设为1000rad/sec,其余为默认值。
Sine Wave1模块:Frequency频率设为1000rad/sec,Sample time采样时间设置为
0.005s,其余为默认值。
Signal Generator模块:Wave form 设置为sawtooth,其余为默认值。
Discrete Filter模块:设置如图所示。
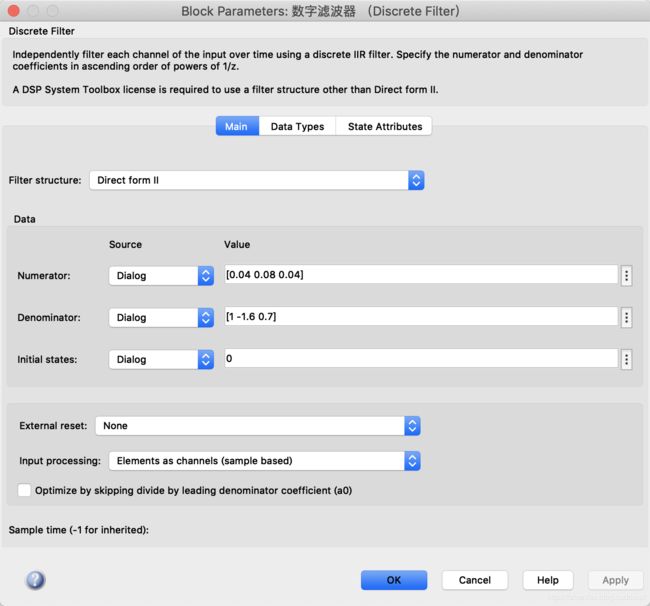
Product模块:默认值。
Product1模块:默认值。
系统仿真时间设置为50s,求解器设为ode45,最大步长设置为0.005。

3.3 系统仿真
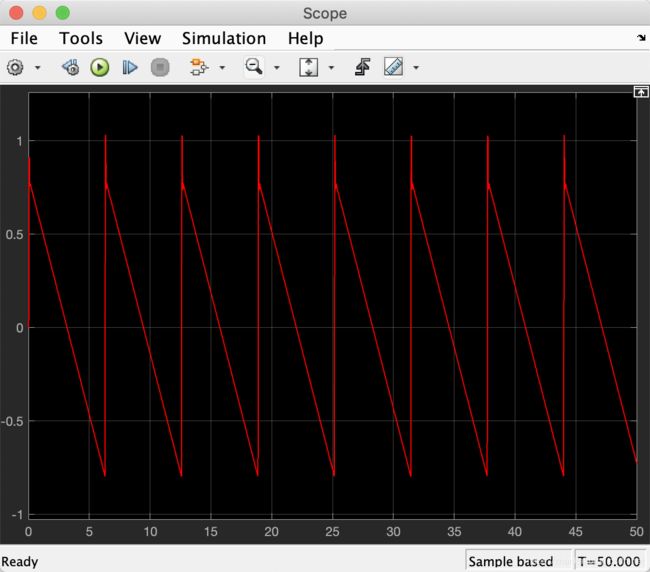
从仿真结果可以看出,滤波器的输出信号和原始锯齿波信号并不完全一致,而是存在一定的失真。这种失真不可避免,因为在实际工作中并不存在理想滤波器。在使用高频载波对低频信号进行调制时,信号间不可避免地会出现干扰。
PS:碰到里面参数设置或者模块的问题可以给我留言,我看到会及时回复的,大家互相交流学习。