深度学习笔记---简单三层CNN的自制框架实现以及对MNIST数据集的训练实现
# 1.简单三层CNN的简易计算图如下
下面的源代码来自《深度学习入门——基于python的理论与实现》
# 2.CNN类的实现
import sys,os
sys.path.append(os.pardir)
import numpy as np
from layers import * # 导入加权和层类Affine、激活函数层类ReLU、卷积层类Convolution、池化层类Pooling
from collections import OrderedDict # 导入有序字典类OrderedDict
# 三层卷积神经网络的实现
class SimpleConvNet:
# 初始化函数,入口参数为输入数据的各维度值、滤波器参数(W1)、隐藏层2的神经元数目、输出层的神经元数目、初始化时权重的标准差
def __init__(self,input_dim=(1,28,28),conv_param={'filter_num':30,'filter_size':5,'pad':0,'stride':1},hidden_size=100,output_size=10,weight_init_std=0.01):
# 第一步 将卷积层的超参数提取出来(方便后面使用),然后计算卷积层的输出大小
filter_num = conv_param['filter_num'] # 滤波器个数30
filter_size = conv_param['filter_size'] # 滤波器大小5*5
filter_pad = conv_param['pad'] # 滤波器填充0
filter_stride = conv_param['stride'] # 滤波器步幅1
input_size = input_dim[1] # 输入数据的大小28
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride +1 # 根据公式计算卷积层输出数据大小
pool_output_size = int(filter_num*(conv_output_size/2)*(conv_output_size/2)) # 根据公式计算池化层输出数据大小
# 第二步 初始化各层权重
self.params = {} # 定义实例变量params为字典型变量
self.params['W1'] = weight_init_std * np.random.randn(filter_num,input_dim[0],filter_size,filter_size) # 第一层权重W1初始化为(滤波器个数*通道数*滤波器高度*滤波器宽度)形状的高斯分布
self.params['b1'] = np.zeros(filter_num) # 第一层偏置b1初始化为长度为卷积层输出数据通道数的一维全0数组
self.params['W2'] = weight_init_std * np.random.randn(pool_output_size,hidden_size) # 第二层权重W2初始化为(池化层输出数据大小*隐藏层2神经元数目)形状的高斯分布
self.params['b2'] = np.zeros(hidden_size) # 第二层偏置b2初始化为长度为隐藏层2神经元数目的一维全0数组
self.params['W3'] = weight_init_std * np.random.randn(hidden_size,output_size) # 第三层权重W3初始化为(隐藏层2神经元数目*输出层神经元数目)形状的高斯分布
self.params['b3'] = np.zeros(output_size) # 第三层偏置b3初始化为长度为输出层神经元数目的一维全0数组
# 第三步 生成搭建神经网络的层
self.layers = OrderedDict() # 定义实例变量layers为有序字典型变量
# 隐藏层1
self.layers['Conv1'] = Convolution(self.params['W1'],self.params['b1'],conv_param['stride'],conv_param['pad']) # 创建卷积层1
self.layers['Relu1'] = ReLU() # 创建激活函数ReLU层1
self.layers['Pool1'] = Pooling(pool_h=2,pool_w=2,stride=2) # 创建池化层1
# 隐藏层2
self.layers['Affine1'] = Affine(self.params['W2'],self.params['b2']) # 创建加权和层1
self.layers['Relu2'] = ReLU() # 创建激活函数ReLU层2
# 输出层
self.layers['Affine2'] = Affine(self.params['W3'],self.params['b3']) # 创建加权和层2
self.last_layer = SoftmaxWithLoss() # 创建softmaxwithloss层
# 推理函数,入口参数为输入数据
def predict(self,x):
for layer in self.layers.values(): # 依次取实例变量layers中的每一层
x = layer.forward(x) # 将前一层的输出作为后一层的输入,进行正向传播,最后得到推理结果y的加权和形式
return x
# 损失函数,入口参数为输入图像数据和正确解标签
def loss(self,x,t):
y = self.predict(x) # 调用推理函数得到推理结果的加权和形式
return self.last_layer.forward(y,t)# 进一步调用最后一层SoftmaxWithLoss的前向函数,得到推理结果的概率形式和损失函数值,这里只返回损失函数值
# 梯度函数,入口参数同loss
def gradient(self,x,t):
# 正向传播
self.loss(x,t) # 得到反向传播所需的各个中间变量
# 反向传播
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定梯度
grads = {}
grads['W1'] = self.layers['Conv1'].dW
grads['b1'] = self.layers['Conv1'].db
grads['W2'] = self.layers['Affine1'].dW
grads['b2'] = self.layers['Affine1'].db
grads['W3'] = self.layers['Affine2'].dW
grads['b3'] = self.layers['Affine2'].db
return grads
# 精度函数,入口参数比loss多了batch_size(批数量大小)
def accuracy(self, x, t, batch_size=100):
if t.ndim != 1 : t = np.argmax(t, axis=1) # 如果正确解标签是one-hot形式,就将其改为简单解形式
acc = 0.0 # 识别正确数的初始值设为0.0
for i in range(int(x.shape[0] / batch_size)): # 对总共600份批数据,一份一份求识别正确的数目,并求和
tx = x[i*batch_size:(i+1)*batch_size]
tt = t[i*batch_size:(i+1)*batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == tt)
return acc / x.shape[0] # 识别正确数/数据总数,返回识别精度
# 3.训练者类的实现
# coding: utf-8
import numpy as np
from optimizer import *
class Trainer:
"""进行神经网络的训练的类
"""
def __init__(self, network, x_train, t_train, x_test, t_test,
epochs=20, mini_batch_size=100,
optimizer='SGD', optimizer_param={'lr':0.01},
evaluate_sample_num_per_epoch=None, verbose=True): # evaluate_sample_num_per_epoch是对于每个epoch,测试样本的数量,默认为整个数据集。verbose=True就打印出提示信息
self.network = network
self.verbose = verbose
self.x_train = x_train
self.t_train = t_train
self.x_test = x_test
self.t_test = t_test
self.epochs = epochs
self.batch_size = mini_batch_size
self.evaluate_sample_num_per_epoch = evaluate_sample_num_per_epoch
# 确定优化器
optimizer_class_dict = {'sgd':SGD, 'momentum':Momentum, 'nesterov':Nesterov,
'adagrad':AdaGrad, 'rmsprpo':RMSprop, 'adam':Adam}
self.optimizer = optimizer_class_dict[optimizer.lower()](**optimizer_param) # 这里利用了可变参数,实际上相当于self.optimizer = Adam(lr=0.01)
self.train_size = x_train.shape[0] # 训练大小设为训练数据集总图片数
self.iter_per_epoch = max(self.train_size / mini_batch_size, 1) # 求出每个epoch的训练次数
self.max_iter = int(epochs * self.iter_per_epoch) # 求出总训练次数
self.current_iter = 0 # 初始化当前训练次数和epoch数
self.current_epoch = 0
self.train_acc_list = [] # 初始化训练数据精度列表和测试数据精度列表,用于绘图
self.test_acc_list = []
def train_step(self): # 单次训练函数
# 从训练数据中随机选择一份批数据
batch_mask = np.random.choice(self.train_size, self.batch_size)
x_batch = self.x_train[batch_mask]
t_batch = self.t_train[batch_mask]
# 计算训练参数的梯度
grads = self.network.gradient(x_batch, t_batch)
# 根据梯度利用优化器更新训练参数
self.optimizer.update(self.network.params, grads)
if self.current_iter % self.iter_per_epoch == 0: # 完成一个epoch,当前epoch数加1,计算并记录当前模型对训练数据和测试数据的识别精度
self.current_epoch += 1
x_train_sample, t_train_sample = self.x_train, self.t_train
x_test_sample, t_test_sample = self.x_test, self.t_test
if not self.evaluate_sample_num_per_epoch is None:
t = self.evaluate_sample_num_per_epoch
x_train_sample, t_train_sample = self.x_train[:t], self.t_train[:t]
x_test_sample, t_test_sample = self.x_test[:t], self.t_test[:t]
train_acc = self.network.accuracy(x_train_sample, t_train_sample)
test_acc = self.network.accuracy(x_test_sample, t_test_sample)
self.train_acc_list.append(train_acc)
self.test_acc_list.append(test_acc)
if self.verbose: print("=== epoch:" + str(self.current_epoch) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc) + " ===")
self.current_iter += 1 # 完成一次训练,当前训练次数加一
def train(self):
for i in range(self.max_iter): # 依次完成所有训练
self.train_step()
print("完成训练",i)
test_acc = self.network.accuracy(self.x_test, self.t_test) # 完成所有训练后测试并打印出当前模型对测试数据的识别精度
if self.verbose:
print("=============== Final Test Accuracy ===============")
print("test acc:" + str(test_acc))
# 4.训练网络的代码
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from simple_convnet import SimpleConvNet
from trainer import Trainer
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False) # 这里没有将MNIST数据集中的图像展平,x_train的形状是(60000,1,28,28)
max_epochs = 20 # 训练次数设置为20个epoch
# 创建简单CNN的对象network
network = SimpleConvNet(input_dim=(1,28,28),
conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
# 创建训练者类对象trainer
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=max_epochs, mini_batch_size=100,
optimizer='Adam', optimizer_param={'lr': 0.001},
evaluate_sample_num_per_epoch=1000)
# 训练者trainer调用train方法对network进行训练
trainer.train()
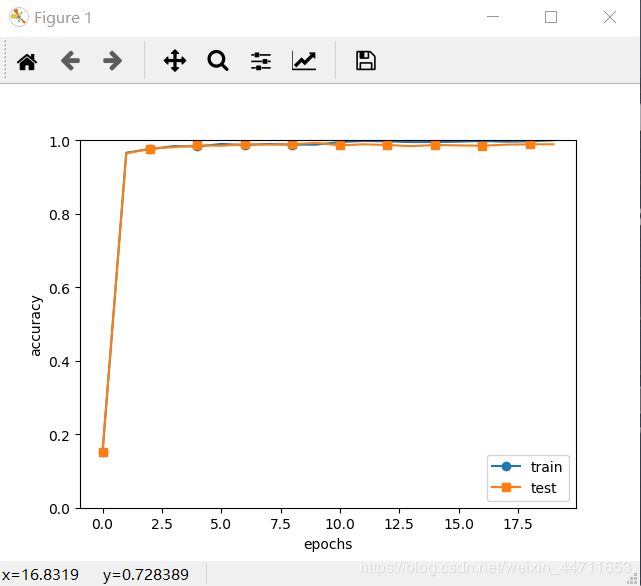
# 绘制训练数据和测试数据的识别精度曲线
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, trainer.train_acc_list, marker='o', label='train', markevery=2)
plt.plot(x, trainer.test_acc_list, marker='s', label='test', markevery=2)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
# 5.运行结果
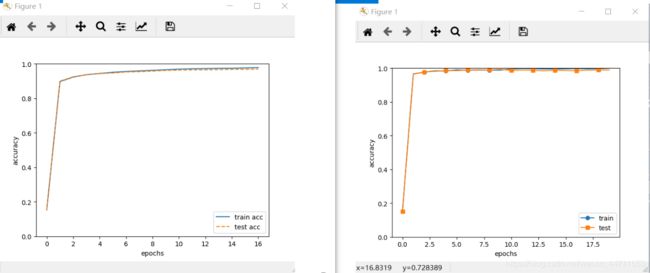
# 6.与普通神经网络的对比
左图是之前单用全连接层实现的神经网络的训练精度变化图,右图是卷积神经网络的训练精度变化图。
不难看出,卷积神经网络最后的识别精度更高,说明卷积神经网络更适用于图像识别。
# 本博客参考了《深度学习入门——基于python的理论与实现》(斋藤康毅著,陆宇杰译),特在此声明。