今天开始学Convex Optimization:第3章 Convex Sets and Convex functions
文章目录
- 第3章 Convex Sets and Convex functions
- 凸优化问题的定义
- 凸集的定义:
- convex hull(凸包) 定义:
- 一些凸集的examples:
- 锥(Cone)和凸锥(Convex Cone)的定义
- 凸集的性质:
- 保凸操作:
- 一个例子:
- Convex Function
- Strictly Convex和Strongly Convex
- 凸函数重要的一阶特性(First-order characterization)
- 凸函数的二阶特性
- Jensen's Inequality
- 保凸操作
- 参考资料
第3章 Convex Sets and Convex functions
凸优化问题的定义
凸集的定义:
定义:给定一个集合 C ⊆ R n C \subseteq \mathbb{R}^n C⊆Rn,满足下列条件则称为凸集: x , y ∈ C ⇒ t x + ( 1 − t ) y ∈ C x,y \in C \Rightarrow tx+(1-t)y \in C x,y∈C⇒tx+(1−t)y∈C 对于任意的 0 ≤ t ≤ 1 0≤t≤1 0≤t≤1

直观上看,可以利用下图帮助理解,假定我们的变量在二维空间中,x,y为二维空间变量,黑体线代表的向量为tx+(1−t)y,t取值范围为[0,1],那么无论t怎么变化,向量tx+(1−t)y总会落在x和y张成的集合空间中。[3]

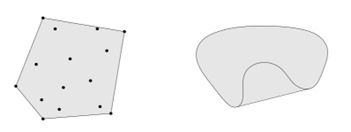
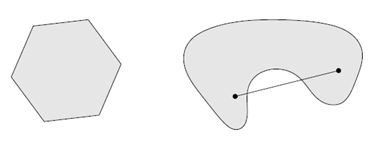
那么从定义出发,我们也能知道非凸集的情况,下图左侧为凸集,右图为非凸集。一句话来概括凸集就是集合内任意两点间连线依旧在集合内。
convex hull(凸包) 定义:
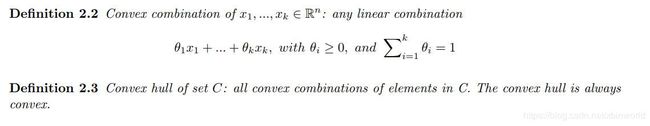
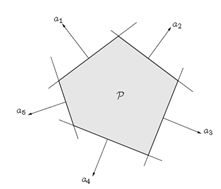
给定集合内的任意k个元素 x 1 , . . . , x k ∈ R n x_1,...,x_k \in \mathbb{R}^n x1,...,xk∈Rn,任意的线性组合形式: θ 1 x 1 + . . . + θ k x k , θ i ≥ 0 , ∑ i = 1 k θ i = 1 \theta_1 x_1+...+\theta_k x_k,\theta_i \geq 0, \sum_{i=1}^{k}\theta_i=1 θ1x1+...+θkxk,θi≥0,∑i=1kθi=1,称之为集合的convex hull,表示为 c o n v ( C ) conv(C) conv(C)。convex hull总是凸的。可以直观认为凸包就是最外围的元素所围成的集合外壳,下图是两个凸包的例子:
一些凸集的examples:
锥(Cone)和凸锥(Convex Cone)的定义
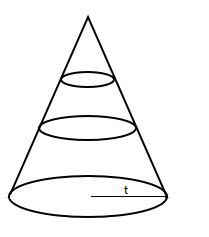
范数锥(Norm cone): { ( x , t ) : ∣ ∣ x ∣ ∣ ≤ t } \left \{(x,t):||x|| \leq t \right \} {(x,t):∣∣x∣∣≤t},对于一范数和二范数成立。下图取定不同的t做出了三维情况下的图
(讨论:这里我感觉用字母 t t t有一些歧义,和上面定义中的 t t t不是一个含义。范数锥中的 t t t是定义域中的一个维度变量;而上面锥定义中的 t t t是表示一个常数):
凸集的性质:
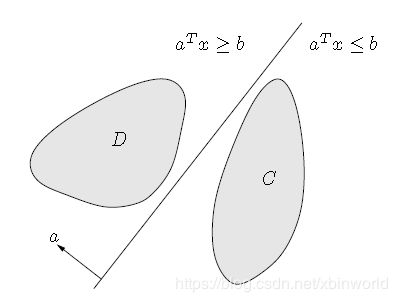
- 可分离超平面理论(Separating hyperplane theorem):两个不相交的凸集总存在一个超平面能将两者分离,如果 C ⋂ D = ∅ C⋂D=∅ C⋂D=∅,那么总存在着a,b使得有: C ⊆ { x : a T x ≤ b } C \subseteq \left \{x:a^Tx \leq b \right \} C⊆{x:aTx≤b}, D ⊆ { x : a T x ≥ b } D \subseteq \left \{x:a^Tx \geq b \right \} D⊆{x:aTx≥b}
- 支撑超平面理论(Supporting hyperplane theorem):凸集边界上的一点必然存在一个支撑超平面穿过该点,即如果C都是非空凸集,
x 0 ∈ b o u n d ( C ) x_0 \in bound(C) x0∈bound(C),那么必然存在一个超平面a,使得, C ⊆ { x : a T x ≤ a T x 0 } C \subseteq \left \{x:a^Tx \leq a^T x_0 \right \} C⊆{x:aTx≤aTx0}。如下图:
保凸操作:
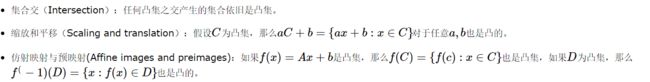
(上面是 f − 1 ( D ) f^{-1}(D) f−1(D),因为借用了[3]的截图,就不重新打了。)
一个例子:
这一章都是一些概念,看的有点晕,哈哈。下面看一下一个证明的例子:
给定一系列的 n × n n\times n n×n的对称矩阵,有一种线性矩阵不等式如下,其中 x ∈ R k x \in R^k x∈Rk。证明: x x x组成的集合C是凸集。
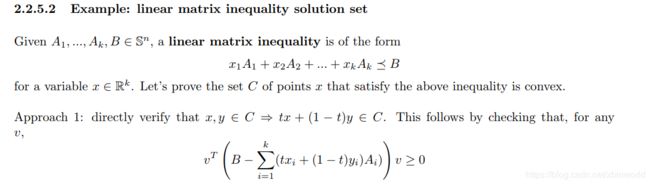
证明过程思路上面写了:只要根据前面提过的凸集定义去证明就行了。如果有 x , y ∈ C x,y \in C x,y∈C,只要证明 t x + ( 1 − t ) y ∈ C tx+(1-t)y \in C tx+(1−t)y∈C,
其中 0 ≤ t ≤ 1 0\leq t \leq 1 0≤t≤1,就可以了。根据题目,我们可以知道:
t v T B v − ∑ i = 1 k t x i v T A i v ≥ 0 ( 1 − t ) v T B v − ∑ i = 1 k ( 1 − t ) y i v T A i v ≥ 0 tv^T B v - \sum_{i=1}^{k}tx_iv^TA_i v \geq 0 \\ (1-t)v^T B v - \sum_{i=1}^{k}(1-t)y_iv^TA_i v \geq 0 tvTBv−i=1∑ktxivTAiv≥0(1−t)vTBv−i=1∑k(1−t)yivTAiv≥0
然后我们可以推出
v T ( B − ∑ i = 1 k ( t x i + ( 1 − t ) y i ) A i ) v = v T B v − ∑ i = 1 k ( t x i + ( 1 − t ) y i ) v T A i v = ( t + ( 1 − t ) ) v T B v − ∑ i = 1 k ( t x i + ( 1 − t ) y i ) v T A i v ≥ 0 v^T \left(B - \sum_{i=1}^{k}(tx_i + (1-t)y_i)A_i \right) v \\ = v^T B v - \sum_{i=1}^{k}(tx_i + (1-t)y_i)v^TA_i v \\ = (t + (1-t))v^T B v - \sum_{i=1}^{k}(tx_i + (1-t)y_i)v^TA_i v \geq 0\\ vT(B−i=1∑k(txi+(1−t)yi)Ai)v=vTBv−i=1∑k(txi+(1−t)yi)vTAiv=(t+(1−t))vTBv−i=1∑k(txi+(1−t)yi)vTAiv≥0
所以 v T ( B − ∑ i = 1 k ( t x i + ( 1 − t ) y i ) A i ) v ≥ 0 v^T \left(B - \sum_{i=1}^{k}(tx_i + (1-t)y_i)A_i \right) v \geq 0 vT(B−∑i=1k(txi+(1−t)yi)Ai)v≥0,即 ∑ i = 1 k ( t x i + ( 1 − t ) y i ) A i ⪯ B \sum_{i=1}^{k}(tx_i + (1-t)y_i)A_i \preceq B ∑i=1k(txi+(1−t)yi)Ai⪯B,即证明了 t x + ( 1 − t ) y ∈ C tx+(1-t)y \in C tx+(1−t)y∈C。所以 x x x组成的集合C是凸集。
Convex Function
定义:给定映射 f : R n → R f:\mathbb{R}^n \rightarrow \mathbb{R} f:Rn→R并且 dom ( f ) ⊆ R n \text{dom} (f) \subseteq \mathbb{R}^n dom(f)⊆Rn为凸集,那么
f ( t x + ( 1 − t ) y ) ≤ t f ( x ) + ( 1 − t ) f ( y ) f(tx+(1-t)y) \leq tf(x)+(1-t)f(y) f(tx+(1−t)y)≤tf(x)+(1−t)f(y) 对于任意 0 ≤ t ≤ 1 0\leq t \leq1 0≤t≤1,且 任意 x , y ∈ dom ( f ) x,y\in \text{dom}(f) x,y∈dom(f)。如下图:
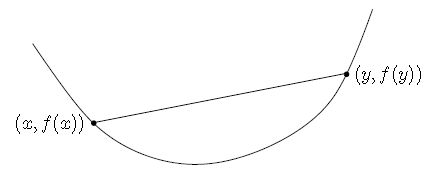
从上图可以看出, f f f的函数值总是位于连接 f ( x ) f(x) f(x)和 f ( y ) f(y) f(y)之间的直线下方。
类比可以理解一下concave函数的定义,很容易得到负的convex函数就是concave函数。
Strictly Convex和Strongly Convex
凸函数重要的一阶特性(First-order characterization)
假设 f f f处处可微,则 f f f为凸函数,当且仅当 dom ( f ) \text{dom}(f) dom(f)为凸,并且对于所有 x , y ∈ dom ( f ) x,y\in \text{dom}(f) x,y∈dom(f)有
f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x ) f(y) \geq f(x)+\nabla f(x)^T(y-x) f(y)≥f(x)+∇f(x)T(y−x)
一阶特性也说明了对于一个可微凸函数 f f f, ∇ f ( x ) = 0 \nabla f(x)= 0 ∇f(x)=0 等价于 x x x minimizes f f f。
证明一阶特性:根据凸函数的定义有(如果 y = x y=x y=x,上面性质显然成立)
f ( t y + ( 1 − t ) x ) ≤ t f ( y ) + ( 1 − t ) f ( x ) f ( t ( y − x ) + x ) − f ( x ) ≤ t ( f ( y ) − f ( x ) ) f(ty+(1-t)x) \leq tf(y)+(1-t)f(x) \\ f(t(y-x)+x) - f(x) \leq t(f(y)-f(x)) \\ f(ty+(1−t)x)≤tf(y)+(1−t)f(x)f(t(y−x)+x)−f(x)≤t(f(y)−f(x))
假设 y − x > 0 y-x > 0 y−x>0可以推出下面结果;如果 y − x < 0 y-x < 0 y−x<0下面的不等号相反,最后得到的结果是一致的。这里我们按照假设 y − x > 0 y-x > 0 y−x>0来推:
f ( t ( y − x ) + x ) − f ( x ) t ( y − x ) ≤ f ( y ) − f ( x ) y − x \frac{f(t(y-x)+x)-f(x)}{t(y-x)}\leq \frac{f(y)-f(x)}{y-x} t(y−x)f(t(y−x)+x)−f(x)≤y−xf(y)−f(x)
观察左边:
lim t → 0 f ( t ( y − x ) + x ) − f ( x ) t ( y − x ) = ∇ f ( x ) \lim_{t\rightarrow0} \frac{f(t(y-x)+x)-f(x)}{t(y-x)}=\nabla f(x) t→0limt(y−x)f(t(y−x)+x)−f(x)=∇f(x)
代入得到:
∇ f ( x ) ( y − x ) ≤ f ( y ) − f ( x ) \nabla f(x)(y-x) \leq f(y)-f(x) ∇f(x)(y−x)≤f(y)−f(x)
所以: f ( y ) ≥ f ( x ) + ∇ f ( x ) ( y − x ) f(y) \geq f(x)+\nabla f(x)(y-x) f(y)≥f(x)+∇f(x)(y−x)
凸函数的二阶特性
二阶特性:如果函数二阶可微分,则 f f f为凸函数,当且仅当 dom ( f ) \text{dom}(f) dom(f)为凸,且对于所有 x ∈ dom ( f ) x\in \text{dom}(f) x∈dom(f) 都有 ∇ 2 f ( x ) ⪰ 0 \nabla^2 f(x)\succeq 0 ∇2f(x)⪰0
Jensen’s Inequality
假若 f f f为凸,并且 X X X由 d o m ( f ) dom(f) dom(f)所支持的随机变量,则有 f ( E [ x ] ) ≤ E [ f ( x ) ] f(E[x])≤E[f(x)] f(E[x])≤E[f(x)]。Jensen’s inequality很重要,可以简单记忆成,期望的函数值小于等于函数的期望,期望也可以用均值来代替。
保凸操作

其中the set S S S is the number of functions f ( x ) f(x) f(x), which can be infinite.

好了,本篇就到这里,借鉴了参考资料中的很多内容。下一章继续。
参考资料
[1] Convexity I: Sets and Functions
[2] http://www.stat.cmu.edu/~ryantibs/convexopt/scribes/convex-fns-scribed.pdf
[3] https://www.cnblogs.com/Lin-chun/p/6875184.html