算法笔试题:(Python实现)------ 算法面试题汇总
算法笔试题:(Python实现)------ 算法面试题汇总
- 算法笔试题:(Python实现)------ 算法面试题汇总
- 开始之前
- Python实现
- 只出现一次的数字
- 多数元素
- 搜索二维矩阵 II
- 合并两个有序数组
- 鸡蛋掉落
- 字符串
- Python实现
- 验证回文串
- 分割回文串
- 单词拆分
- 单词拆分 II
- 实现 Trie (前缀树)
- 单词搜索 II
- 有效的字母异位词
- 字符串中的第一个唯一字符
- 数组
- Python实现
- 乘积最大子序列
- 多数元素
- 存在重复元素
- 移动零
- 打乱数组
- 两个数组的交集 II
- 递增的三元子序列
- 搜索二维矩阵 II
- 除自身以外数组的乘积
- 堆、栈与队列
- Python实现
- 数组中的第K个最大元素
- 数据流的中位数
- 有序矩阵中第K小的元素
- 前 K 个高频元素
- 滑动窗口最大值
- 基本计算器 II
- 扁平化嵌套列表迭代器
- 逆波兰表达式求值
- 链表
- 复制带随机指针的链表
- 环形链表
- 排序链表
- 排序链表
- 相交链表
- 反转链表
- 回文链表
- 删除链表中的节点
- 奇偶链表
- 哈希与映射
- Python实现
- Excel表列序号
- 常数时间插入、删除和获取随机元素
- 四数相加 II
- 树
- Python实现
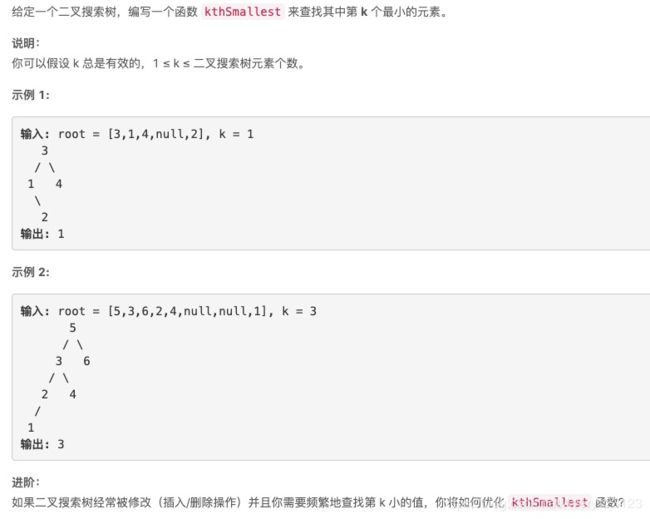
- 二叉搜索树中第K小的元素
- 二叉树的最近公共祖先
- 二叉树的序列化与反序列化
- 天际线问题
- 排序与检索
- Python实现
- 最大数
- 摆动排序 II
- 寻找峰值
- 寻找重复数
- 计算右侧小于当前元素的个数
- 动态规划
- Python实现
- 打家劫舍
- 完全平方数
- 最长上升子序列
- 零钱兑换
- 最长连续序列
- 二叉树中的最大路径和
- 矩阵中的最长递增路径
- 至少有K个重复字符的最长子串
- 图论
- Python实现
- 岛屿数量
- 课程表
- 课程表 II
- 单词接龙
- 单词接龙 II
- 数学问题
- 直线上最多的点数
- 分数到小数
- 阶乘后的零
- 颠倒二进制位
- 位1的个数
- 计数质数
- 缺失数字
- 3的幂
算法笔试题:(Python实现)------ 算法面试题汇总
开始之前
Python实现
只出现一次的数字
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [3,2,3]
输出: 3
示例 2:
输入: [2,2,1,1,1,2,2]
输出: 2
class Solution(object):
def singleNumber(self,nums):
nums_dict = {}
if not nums:
return None
for i in nums:
if i not in nums_dict:
nums_dict[i] = 1
else:
nums_dict[i] += 1
for i in nums_dict.keys():
if nums_dict[i] == 1:
return i
多数元素
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [3,2,3]
输出: 3
示例 2:
输入: [2,2,1,1,1,2,2]
输出: 2
排序法:
class Solution(object):
def majorityElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
nums = sorted(nums)
return nums[len(nums)//2]
统计法:
class Solution(object):
def majorityElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
count = 0
candi = 0
for i in nums:
if i == candi:
count += 1
else:
if count == 0:
candi = i
count = 1
else:
count -= 1
return candi
搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例:
现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
class Solution(object):
def searchMatrix(self, matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
if not matrix or matrix ==[[]]:
return False
for i in range(len(matrix)):
if matrix[i].count(target):
return True
if i == len(matrix)-1:
return False
else:
continue
合并两个有序数组
给定两个有序整数数组 nums1 和 nums2,将 nums2 合并到 nums1 中,使得 num1 成为一个有序数组。
说明:
初始化 nums1 和 nums2 的元素数量分别为 m 和 n。
你可以假设 nums1 有足够的空间(空间大小大于或等于 m + n)来保存 nums2 中的元素。
示例:
输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
输出: [1,2,2,3,5,6]
class Solution(object):
def merge(self, nums1, m, nums2, n):
"""
:type nums1: List[int]
:type m: int
:type nums2: List[int]
:type n: int
:rtype: None Do not return anything, modify nums1 in-place instead.
"""
while n > 0 and m >0:
if nums1[m-1] >= nums2[n-1]:
nums1[m+n-1] = nums1[m-1]
m-=1
else:
nums1[m+n-1] = nums2[n-1]
n -= 1
if m == 0:
for i in range(n):
nums1[i] = nums2[i]
鸡蛋掉落
你将获得 K 个鸡蛋,并可以使用一栋从 1 到 N 共有 N 层楼的建筑。
每个蛋的功能都是一样的,如果一个蛋碎了,你就不能再把它掉下去。
你知道存在楼层 F ,满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎,从 F 楼层或比它低的楼层落下的鸡蛋都不会破。
每次移动,你可以取一个鸡蛋(如果你有完整的鸡蛋)并把它从任一楼层 X 扔下(满足 1 <= X <= N)。
你的目标是确切地知道 F 的值是多少。
无论 F 的初始值如何,你确定 F 的值的最小移动次数是多少?
示例 1:
输入:K = 1, N = 2
输出:2
解释:
鸡蛋从 1 楼掉落。如果它碎了,我们肯定知道 F = 0 。
否则,鸡蛋从 2 楼掉落。如果它碎了,我们肯定知道 F = 1 。
如果它没碎,那么我们肯定知道 F = 2 。
因此,在最坏的情况下我们需要移动 2 次以确定 F 是多少。
示例 2:
输入:K = 2, N = 6
输出:3
示例 3:
输入:K = 3, N = 14
输出:4
提示:
1 <= K <= 100
1 <= N <= 10000
class Solution(object):
def superEggDrop(self,K,N):
#构建二维数组DP
DP = [[0 for _ in range(N+1)] for _ in range(K+1)]
for i in range(1,K+1):
for step in range(1,N+1):
DP[i][step] = DP[i-1][step-1] + (DP[i][step-1]+1)
if DP[K][step] >= N:
return step
return 0
字符串
Python实现
验证回文串
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
说明:本题中,我们将空字符串定义为有效的回文串。
示例 1:
输入: "A man, a plan, a canal: Panama"
输出: true
示例 2:
输入: "race a car"
输出: false
class Solution(object):
def isPalindrome(self, s):
"""
:type s: str
:rtype: bool
"""
s = s.lower()
chexk = []
for i in s:
if i.isalpha() or i.isdigit():
chexk.append(i)
lens = len(chexk)//2
for i in range(lens):
if chexk[i] != chexk[len(chexk)-1-i]:
return False
return True
分割回文串
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
输入: "aab"
输出:
[
["aa","b"],
["a","a","b"]
]
class Solution(object):
def partition(self, s):
"""
:type s: str
:rtype: List[List[str]]
"""
return self.dfs(s)
def dfs(self,s):
if s == '':
return [[]]
res = []
for i in range(len(s)):
if self.isPal(s[:i+1]):
tmp_set = self.dfs(s[i+1:])
for tmp in tmp_set:
res.append([s[:i+1]]+tmp)
return res
def isPal(self,s):
if s == s[::-1]:
return True
return False
单词拆分
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明:
拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1:
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
示例 2:
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
注意你可以重复使用字典中的单词。
示例 3:
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false
动态规划:
class Solution(object):
def wordBreak(self, s, wordDict):
"""
:type s: str
:type wordDict: List[str]
:rtype: bool
"""
if not s:
return True
length = len(s)
dp = [False for _ in range(length+1)]
dp[0] = True
for i in range(1,length+1):
for j in range(i):
if dp[j] and s[j:i] in wordDict:
dp[i] =True
break
return dp[-1]
单词拆分 II
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,在字符串中增加空格来构建一个句子,使得句子中所有的单词都在词典中。返回所有这些可能的句子。
说明:
分隔时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1:
输入:
s = "catsanddog"
wordDict = ["cat", "cats", "and", "sand", "dog"]
输出:
[
"cats and dog",
"cat sand dog"
]
示例 2:
输入:
s = "pineapplepenapple"
wordDict = ["apple", "pen", "applepen", "pine", "pineapple"]
输出:
[
"pine apple pen apple",
"pineapple pen apple",
"pine applepen apple"
]
解释: 注意你可以重复使用字典中的单词。
示例 3:
输入:
s = "catsandog"
wordDict = ["cats", "dog", "sand", "and", "cat"]
输出:
[]
递归+构建额外字典保存切分结果
class Solution(object):
def wordBreak(self, s, wordDict):
"""
:type s: str
:type wordDict: List[str]
:rtype: List[str]
"""
res = []
memo = dict()
return self.dfs(s,res,wordDict,memo)
def dfs(self,s,res,wordDict,memo):
if s in memo:
return memo[s]
if not s:
return [""]
res = []
for word in wordDict:
if s[:len(word)] != word:
continue
for r in self.dfs(s[len(word):],res,wordDict,memo):
res.append(word+("" if not r else " "+r))
memo[s] = res
return res
实现 Trie (前缀树)
实现一个 Trie (前缀树),包含 insert, search, 和 startsWith 这三个操作。
示例:
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 true
trie.search("app"); // 返回 false
trie.startsWith("app"); // 返回 true
trie.insert("app");
trie.search("app"); // 返回 true
说明:
你可以假设所有的输入都是由小写字母 a-z 构成的。
保证所有输入均为非空字符串。
class Trie(object):
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = {}
def insert(self, word):
"""
Inserts a word into the trie.
:type word: str
:rtype: None
"""
node = self.root
for char in word:
node = node.setdefault(char,{})
node["end"] = True
def search(self, word):
"""
Returns if the word is in the trie.
:type word: str
:rtype: bool
"""
node = self.root
for char in word:
if char not in node:
return False
node = node[char]
return "end" in node
def startsWith(self, prefix):
"""
Returns if there is any word in the trie that starts with the given prefix.
:type prefix: str
:rtype: bool
"""
node = self.root
for char in prefix:
if char not in node:
return False
node = node[char]
return True
# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)
单词搜索 II
给定一个二维网格 board 和一个字典中的单词列表 words,找出所有同时在二维网格和字典中出现的单词。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。
示例:
输入:
words = ["oath","pea","eat","rain"] and board =
[
['o','a','a','n'],
['e','t','a','e'],
['i','h','k','r'],
['i','f','l','v']
]
输出: ["eat","oath"]
说明:
你可以假设所有输入都由小写字母 a-z 组成。
提示:
你需要优化回溯算法以通过更大数据量的测试。你能否早点停止回溯?
如果当前单词不存在于所有单词的前缀中,则可以立即停止回溯。什么样的数据结构可以有效地执行这样的操作?散列表是否可行?为什么? 前缀树如何?如果你想学习如何实现一个基本的前缀树,请先查看这个问题: 实现Trie(前缀树)。
解法:前缀树 + dfs(深度优先搜索)
class Trie(object):
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = {}
def insert(self, word):
"""
Inserts a word into the trie.
:type word: str
:rtype: None
"""
node = self.root
for char in word:
node = node.setdefault(char, {})
node["end"] = True
def search(self, word):
"""
Returns if the word is in the trie.
:type word: str
:rtype: bool
"""
node = self.root
for char in word:
if char not in node:
return False
node = node[char]
return "end" in node
def startsWith(self, prefix):
"""
Returns if there is any word in the trie that starts with the given prefix.
:type prefix: str
:rtype: bool
"""
node = self.root
for char in prefix:
if char not in node:
return False
node = node[char]
return True
class Solution(object):
def findWords(self, board, words):
"""
:type board: List[List[str]]
:type words: List[str]
:rtype: List[str]
"""
if not board or not board[0]:
return []
m, n = len(board), len(board[0])
dx = [1, -1, 0, 0]
dy = [0, 0, 1, -1]
tree = Trie()
for word in words:
tree.insert(word)
words = set(words)
res = set()
def dfs(x0, y0, node, tmpword):
visited.add((x0, y0))
for k in range(4):
x = x0 + dx[k]
y = y0 + dy[k]
if 0 <= x < m and 0 <= y < n and board[x][y] in node and (x, y) not in visited:
visited.add((x, y))
dfs(x, y, node[board[x][y]], tmpword + board[x][y])
visited.remove((x,y))
if tmpword in words: #找到一个单词了
res.add(tmpword) #用集合避免重复
for i in range(m):
for j in range(n):
if board[i][j] in tree.root:
visited = set((i,j))
dfs(i, j, tree.root[board[i][j]], board[i][j])
return list(res)
有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
示例 1:
输入: s = “anagram”, t = “nagaram”
输出: true
示例 2:
输入: s = “rat”, t = “car”
输出: false
说明:
你可以假设字符串只包含小写字母。
进阶:
如果输入字符串包含 unicode 字符怎么办?你能否调整你的解法来应对这种情况?
class Solution(object):
def isAnagram(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
s = sorted(s)
t = sorted(t)
if len(s) != len( t):
return False
for i in range(len(s)):
if s[i] != t[i]:
return False
return True
字符串中的第一个唯一字符
给定一个字符串,找到它的第一个不重复的字符,并返回它的索引。如果不存在,则返回 -1。
案例:
s = “leetcode”
返回 0.
s = “loveleetcode”,
返回 2.
注意事项:您可以假定该字符串只包含小写字母。
class Solution(object):
def firstUniqChar(self,s):
my_dict = {}
for i in s:
if i not in my_dict:
my_dict[i] = 1
else:
my_dict[i] += 1
for i in range(len(s)):
if my_dict[s[i]] == 1:
return i
return -1
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
示例 1:
输入:["h","e","l","l","o"]
输出:["o","l","l","e","h"]
示例 2:
输入:["H","a","n","n","a","h"]
输出:["h","a","n","n","a","H"]
class Solution(object):
def reverseString(self, s):
"""
:type s: List[str]
:rtype: None Do not return anything, modify s in-place instead.
"""
lens = len(s)//2
for i in range(lens):
s[i],s[len(s)-1-i] = s[len(s)-1-i],s[i]
数组
Python实现
乘积最大子序列
给定一个整数数组 nums ,找出一个序列中乘积最大的连续子序列(该序列至少包含一个数)。
示例 1:
输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
思路:典型的 “动态规划” (Dynamic Planning) 问题。
通过2个1维数组来分别记录,最大值dp_max和最小值dp_min 序列‘:
class Solution(object):
def maxProduct(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if not nums:
return 0
n = len(nums)
if n < 2:
return nums[0]
maxRes = nums[0]
dp_max = [nums[0]]*n
dp_min = [nums[0]]*n
for i in range(1,n):
dp_max[i] = max(dp_max[i-1]*nums[i],nums[i],dp_min[i-1]*nums[i])
dp_min[i] = min(dp_max[i-1]*nums[i],nums[i],dp_min[i-1]*nums[i])
maxRes = max(dp_max[i],maxRes)
return maxRes
通过1个2维数组dp_nums同时记录最大和最小序列:
class Solution(object):
def maxProduct(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if not nums:
return 0
n = len(nums)
if n < 2:
return nums[0]
maxRes = nums[0]
dp_nums = [[0,0] for _ in range(n)]
dp_nums[0][0], dp_nums[0][1] = nums[0], nums[0]
for i in range(1, n):
dp_nums[i][0] = max(dp_nums[i-1][0]*nums[i], nums[i], dp_nums[i-1][1]*nums[i])
dp_nums[i][1] = min(dp_nums[i-1][0]*nums[i], nums[i], dp_nums[i-1][1]*nums[i])
maxRes = max(dp_nums[i][0], maxRes)
return maxRes
多数元素
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [3,2,3]
输出: 3
示例 2:
输入: [2,2,1,1,1,2,2]
输出: 2
class Solution(object):
def majorityElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
my_dict = {}
for i in range(len(nums)):
if nums[i] in my_dict:
my_dict[nums[i]] += 1
else:
my_dict[nums[i]] = 1
for i in my_dict.keys():
if my_dict[i] == max(my_dict.values()):
return i
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
示例 1:
输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入: [-1,-100,3,99] 和 k = 2
输出: [3,99,-1,-100]
解释:
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]
class Solution(object):
def rotate(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: None Do not return anything, modify nums in-place instead.
"""
l = len(nums)
k = k%l
nums[:] = nums[l-k:]+nums[:l-k]
return nums
存在重复元素
给定一个整数数组,判断是否存在重复元素。
如果任何值在数组中出现至少两次,函数返回 true。如果数组中每个元素都不相同,则返回 false。
示例 1:
输入: [1,2,3,1]
输出: true
示例 2:
输入: [1,2,3,4]
输出: false
示例 3:
输入: [1,1,1,3,3,4,3,2,4,2]
输出: true
class Solution(object):
def containsDuplicate(self,nums):
if len(nums) > len(set(nums)):
return True
else:
return False
移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:
必须在原数组上操作,不能拷贝额外的数组。
尽量减少操作次数。
class Solution(object):
def moveZeroes(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
j = 0
for i in range(len(nums)):
if nums[i] != 0:
nums[i],nums[j] = nums[j],nums[i]
j+=1
打乱数组
打乱一个没有重复元素的数组。
示例:
// 以数字集合 1, 2 和 3 初始化数组。
int[] nums = {1,2,3};
Solution solution = new Solution(nums);
// 打乱数组 [1,2,3] 并返回结果。任何 [1,2,3]的排列返回的概率应该相同。
solution.shuffle();
// 重设数组到它的初始状态[1,2,3]。
solution.reset();
// 随机返回数组[1,2,3]打乱后的结果。
solution.shuffle();
import copy
import random
class Solution(object):
def __init__(self,nums):
self._item = nums
def reset(self):
return self._item
def shuffle(self):
res = []
temp = copy.deepcopy(self._item)
while len(temp) != 0:
toInsert = temp[random.randint(0,len(temp)-1)]
res.append(toInsert)
temp.remove(toInsert)
return res
两个数组的交集 II
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
输入: nums1 = [1,2,2,1], nums2 = [2,2]
输出: [2,2]
示例 2:
输入: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出: [4,9]
说明:
输出结果中每个元素出现的次数,应与元素在两个数组中出现的次数一致。
我们可以不考虑输出结果的顺序。
进阶:
如果给定的数组已经排好序呢?你将如何优化你的算法?
如果 nums1 的大小比 nums2 小很多,哪种方法更优?
如果 nums2 的元素存储在磁盘上,磁盘内存是有限的,并且你不能一次加载所有的元素到内存中,你该怎么办?
class Solution(object):
def intersect(self,nums1,nums2):
nums1 = sorted(nums1)
nums2 = sorted(nums2)
res = []
i,j=0,0
while i <len(nums1) and j <len(nums2):
if nums1[i] == nums2[j]:
res.append(nums1[i])
i+=1
j+=1
elif nums1[i] < nums2[j]:
i += 1
else:
j += 1
return res
递增的三元子序列
给定一个未排序的数组,判断这个数组中是否存在长度为 3 的递增子序列。
数学表达式如下:
如果存在这样的 i, j, k, 且满足 0 ≤ i < j < k ≤ n-1,
使得 arr[i] < arr[j] < arr[k] ,返回 true ; 否则返回 false 。
说明: 要求算法的时间复杂度为 O(n),空间复杂度为 O(1) 。
示例 1:
输入: [1,2,3,4,5]
输出: true
示例 2:
输入: [5,4,3,2,1]
输出: false
class Solution(object):
def increasingTriplet(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
if len(nums) <= 2:
return False
min = nums[0]
mid = 9999999999
for i in nums:
if i <= min:
min = i
elif i <= mid:
mid = i
if mid < i and min < mid:
return True
return False
搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例:
现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
class Solution(object):
def searchMatrix(self, matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
if not matrix or not matrix[0]:
return False
for i in range(len(matrix)):
if matrix[i].count(target):
return True
if i == len(matrix)-1:
return False
else:
continue
除自身以外数组的乘积
class Solution(object):
def productExceptSelf(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
n = len(nums)
l,r = 1,1
res = [1]*n
for i in range(n):
res[i] = l
l *= nums[i]
for i in range(n)[::-1]:
res[i] *= r
r *= nums[i]
return res
堆、栈与队列
Python实现
数组中的第K个最大元素
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:
你可以假设 k 总是有效的,且 1 ≤ k ≤ 数组的长度。
利用Python的sort:
class Solution(object):
def findKthLargest(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: int
"""
nums.sort()
return nums[-k]
数据流的中位数
中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例:
addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2
进阶:
如果数据流中所有整数都在 0 到 100 范围内,你将如何优化你的算法?
如果数据流中 99% 的整数都在 0 到 100 范围内,你将如何优化你的算法?
解法1:笨办法,每次计算中位数之前,对数组排序一次
class MedianFinder(object):
def __init__(self):
"""
initialize your data structure here.
"""
self.array = []
def addNum(self, num):
"""
:type num: int
:rtype: None
"""
self.array.append(num)
def findMedian(self):
"""
:rtype: float
"""
self.array.sort()
n = len(self.array)
if n % 2 == 1:
return self.array[n//2]
else:
return (self.array[n//2] + self.array[n//2 - 1]) /2.0
# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()
有序矩阵中第K小的元素
给定一个 n x n 矩阵,其中每行和每列元素均按升序排序,找到矩阵中第k小的元素。
请注意,它是排序后的第k小元素,而不是第k个元素。
示例:
matrix = [
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
],
k = 8,
返回 13。
说明:
你可以假设 k 的值永远是有效的, 1 ≤ k ≤ n2 。
解法1:遍历+排序
class Solution(object):
def kthSmallest(self, matrix, k):
"""
:type matrix: List[List[int]]
:type k: int
:rtype: int
"""
l = []
for i in range(len(matrix)):
for j in range(len(matrix[0])):
l.append(matrix[i][j])
l.sort()
return l[k-1]
解法2:堆
import heapq
class Solution(object):
def kthSmallest(self, matrix, k):
"""
:type matrix: List[List[int]]
:type k: int
:rtype: int
"""
heap = []
heapq.heapify(heap)
def heap_add(num):
if len(heap) >= k:
heapq.heappop(heap)
heapq.heappush(heap,-num)
for row in matrix:
if len(heap) >= k and row[0] >= -heap[0]:
break
for col in row:
if len(heap) >= k and col >= -heap[0]:
break
heap_add(col)
return -heap[0]
前 K 个高频元素
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
说明:
你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
class Solution(object):
def topKFrequent(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: List[int]
"""
if len(nums) == 0:
return []
dic = {}
for num in nums:
if num in dic:
dic[num] += 1
else:
dic[num] = 1
l = sorted(dic.items(),key=lambda x:x[1],reverse = True)
return [item[0] for item in l[:k]]
滑动窗口最大值
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
提示:
你可以假设 k 总是有效的,在输入数组不为空的情况下,1 ≤ k ≤ 输入数组的大小。
进阶:
你能在线性时间复杂度内解决此题吗?
解法1:常规思路,时间复杂度O(N)
class Solution(object):
def maxSlidingWindow(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: List[int]
"""
if len(nums) == 0:
return []
if k == 1:
return nums
res = []
res.append(max(nums[:k]))
for i in range(1,len(nums)-k+1):
m = max(nums[i:i+k])
res.append(m)
return res
解法2:通过 “双端队列” ,也就是两边都能进能出的队列。
首先就是入队列,每次滑动窗口都把最大值左边小的数踢掉,也就是出队,后面再滑动窗口进行维护,这样相当于就是每一个数走过场。时间复杂度就是O(N*1)
class Solution(object):
def maxSlidingWindow(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: List[int]
"""
if not nums:
return []
window, res = [], []
for i, num in enumerate(nums):
# 窗口滑动时的规律
if i>=k and window[0] <= i-k:
window.pop(0)
# 把最大值左边的数小的清除
while window and nums[window[-1]] <= num:
window.pop()
window.append(i)
if i >= k-1:
res.append(nums[window[0]])
return res
基本计算器 II
实现一个基本的计算器来计算一个简单的字符串表达式的值。
字符串表达式仅包含非负整数,+, - ,*,/ 四种运算符和空格 。 整数除法仅保留整数部分。
示例 1:
输入: "3+2*2"
输出: 7
示例 2:
输入: " 3/2 "
输出: 1
示例 3:
输入: " 3+5 / 2 "
输出: 5
说明:
你可以假设所给定的表达式都是有效的。
请不要使用内置的库函数 eval。
解法1:先用 eval() 处理看下结果,当然题目不允许
eval() 函数用来执行一个字符串表达式,并返回表达式的值。
eval() 方法的语法: eval(expression[, globals[, locals]])
参数:
expression – 表达式。
globals – 变量作用域,全局命名空间,如果被提供,则必须是一个字典对象。
locals – 变量作用域,局部命名空间,如果被提供,可以是任何映射对象。
class Solution(object):
def calculate(self, s):
"""
:type s: str
:rtype: int
"""
# 题目要求除法只保留整数部分,所以将除号“/”调整为整除符“//”
return eval(s.replace("/", "//"))
解法2#:把所有加减乘除运算转化“加法”运算
class Solution(object):
def calculate(self, s):
def add(x,y):
return x+y
def minus(x,y):
return x-y
def multiply(x,y):
return x*y
def divide(x,y):
return x//y
opes={'+':add,'-':minus,'*':multiply,'/':divide}
sta_nums=[]
sta_opes=[]
numstr=''
for si in s:
if si==' ':
continue
if si>='0' and si<='9':
numstr=numstr+si
continue
else:
num=int(numstr)
numstr=''
if (len(sta_opes)>0 and sta_opes[-1] in [multiply,divide]):
x=sta_nums.pop()
ope=sta_opes.pop()
num=ope(x,num)
sta_nums.append(num)
sta_opes.append(opes[si])
num=int(numstr)
if (len(sta_opes)>0 and sta_opes[-1] in [multiply,divide]):
x=sta_nums.pop()
ope=sta_opes.pop()
num=ope(x,num)
sta_nums.append(num)
res=sta_nums.pop(0)
while (len(sta_opes)>0):
ope=sta_opes.pop(0)
y=sta_nums.pop(0)
res=ope(res,y)
return res
扁平化嵌套列表迭代器
给你一个嵌套的整型列表。请你设计一个迭代器,使其能够遍历这个整型列表中的所有整数。
列表中的每一项或者为一个整数,或者是另一个列表。
示例 1:
输入: [[1,1],2,[1,1]]
输出: [1,1,2,1,1]
解释: 通过重复调用 next 直到 hasNext 返回 false,next 返回的元素的顺序应该是: [1,1,2,1,1]。
示例 2:
输入: [1,[4,[6]]]
输出: [1,4,6]
解释: 通过重复调用 next 直到 hasNext 返回 false,next 返回的元素的顺序应该是: [1,4,6]。
思路:
利用栈后进先出的性质,每次要next的时候通过循环处理保证栈顶为数字。
# """
# This is the interface that allows for creating nested lists.
# You should not implement it, or speculate about its implementation
# """
# class NestedInteger(object):
# def isInteger(self):
# """
# @return True if this NestedInteger holds a single integer, rather than a nested list.
# :rtype bool
# """
#
# def getInteger(self):
# """
# @return the single integer that this NestedInteger holds, if it holds a single integer
# Return None if this NestedInteger holds a nested list
# :rtype int
# """
#
# def getList(self):
# """
# @return the nested list that this NestedInteger holds, if it holds a nested list
# Return None if this NestedInteger holds a single integer
# :rtype List[NestedInteger]
# """
class NestedIterator(object):
def __init__(self, nestedList):
"""
Initialize your data structure here.
:type nestedList: List[NestedInteger]
"""
if nestedList:
self.stack = nestedList[::-1]
else:
self.stack = []
def next(self):
"""
:rtype: int
"""
return self.stack.pop()
def hasNext(self):
"""
:rtype: bool
"""
if self.stack:
top = self.stack.pop()
while not top.isInteger():
self.stack += top.getList()[::-1]
if self.stack:
top = self.stack.pop()
else:
return False
self.stack.append(top)
return True
else:
return False
# Your NestedIterator object will be instantiated and called as such:
# i, v = NestedIterator(nestedList), []
# while i.hasNext(): v.append(i.next())
逆波兰表达式求值
根据逆波兰表示法,求表达式的值。
有效的运算符包括 +, -, *, / 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入: ["2", "1", "+", "3", "*"]
输出: 9
解释: ((2 + 1) * 3) = 9
示例 2:
输入: ["4", "13", "5", "/", "+"]
输出: 6
解释: (4 + (13 / 5)) = 6
示例 3:
输入: ["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"]
输出: 22
解释:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
class Solution:
def evalRPN(self, tokens):
"""
:type tokens: List[str]
:rtype: int
"""
def add(x,y):
return x+y
def sub(x,y):
return x-y
def mul(x,y):
return x*y
def div(x,y):
if x*y < 0:
return -(-x/y)
else:
return x/y
stack = []
ops = {"+":add,"-":sub,"*":mul,"/":div}
for char in tokens:
if char in ops:
t1 = int(stack.pop())
t2 = int(stack.pop())
stack.append(ops[char](t2,t1))
else:
stack.append(char)
return int(stack.pop())
链表
复制带随机指针的链表
给定一个链表,每个节点包含一个额外增加的随机指针,该指针可以指向链表中的任何节点或空节点。
要求返回这个链表的 深拷贝。
我们用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示 Node.val 的整数。
random_index:随机指针指向的节点索引(范围从 0 到 n-1);如果不指向任何节点,则为 null 。
示例 1:
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
示例 2:
输入:head = [[1,1],[2,1]]
输出:[[1,1],[2,1]]
示例 3:
输入:head = [[3,null],[3,0],[3,null]]
输出:[[3,null],[3,0],[3,null]]
示例 4:
输入:head = []
输出:[]
解释:给定的链表为空(空指针),因此返回 null。
提示:
-10000 <= Node.val <= 10000
Node.random 为空(null)或指向链表中的节点。
节点数目不超过 1000 。
class RandomListNode(object):
def __init__(self,x):
self.val = x
self.next = None
self.random = None
class Solution(object):
def copyRandomList(self, head):
"""
:type head: RandomListNode
:rtype: RandomListNode
"""
dummy = RandomListNode(0)
ori = head
cp = dummy
ori_cp_dict = {}
while ori:
cp.next = RandomListNode(ori.val)
cp.next.random = ori.random
ori_cp_dict[ori] = cp.next
ori = ori.next
cp = cp.next
cp = dummy.next
while cp:
if cp.random:
cp.random = ori_cp_dict[cp.random]
cp = cp.next
return dummy.next
环形链表
给定一个链表,判断链表中是否有环。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
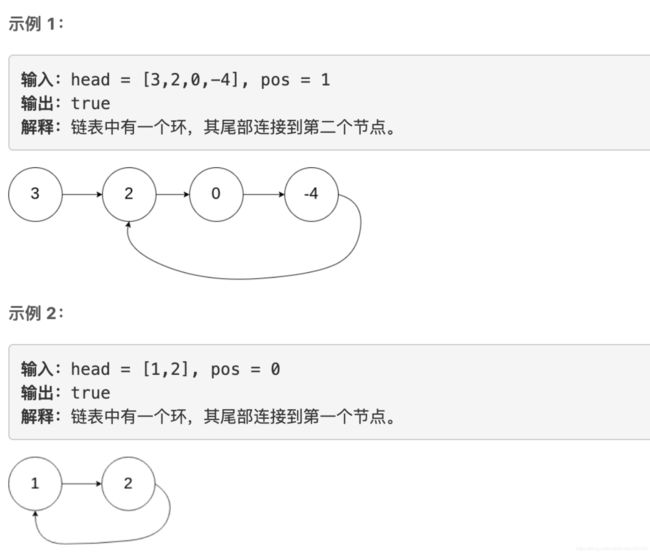

class Solution(object):
def hasCycle(self,head):
"""
:type head: ListNode
:rtype: bool
"""
if head == None or head.next == None:
return False
fast = slow = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
if slow == fast:
return True
return False
排序链表
在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序。
示例 1:
输入: 4->2->1->3
输出: 1->2->3->4
示例 2:
输入: -1->5->3->4->0
输出: -1->0->3->4->5
排序链表
思路:
这就需要分析一下各个排序算法的复杂度了。时间复杂度在O(nlogN)的排序算法是快速排序,堆排序,归并排序。但是快排的最坏时间复杂度是O(n^2),平均时间复杂度为O(nlogn),所以不考虑快速排序。而堆排序太繁琐了。。。。。emmm。。。生硬地排除了。对于数组来说占用的空间复杂度为O(1),O(n),O(n)。但是对于链表来说使用归并排序占用空间为O(1).
快慢指针找到链表中点
class ListNode(object):
def __init__(self,x):
self.val = x
self.next = None
class Solution(object):
def sortList(self,head):
if head is None or head.next is None:
return head
mid = self.get_mid(head)
l = head
r = mid.next
mid.next = None
return self.merge(self.sortList(l),self.sortList(r))
def merge(self,p,q):
tmp = ListNode(0)
h = tmp
while p and q:
if p.val < q.val:
h.next = p
p = p.next
else:
h.next = q
q = q.next
h = h.next
if p:
h.next = p
if q:
h.next = q
return tmp.next
def get_mid(self,node):
if node is None:
return None
fast = slow = node
while fast.next and fast.next.next:
slow = slow.next
fast = fast.next.next
return slow
相交链表
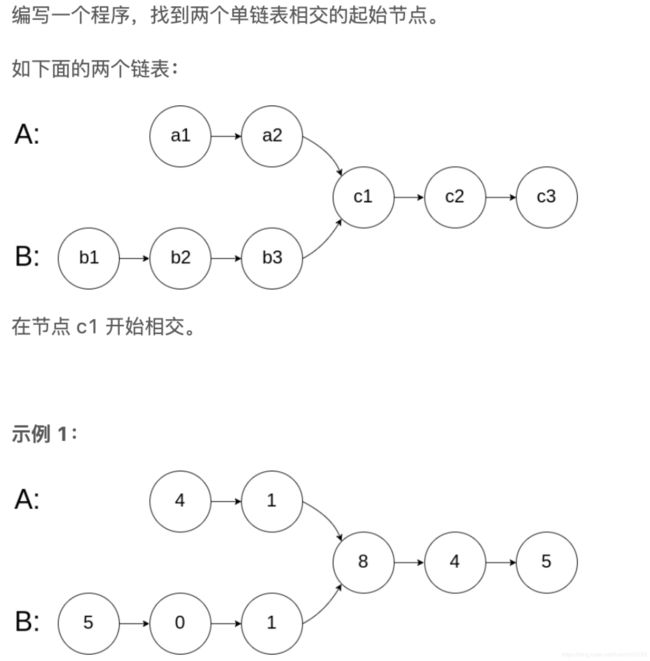
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Reference of the node with value = 8
输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
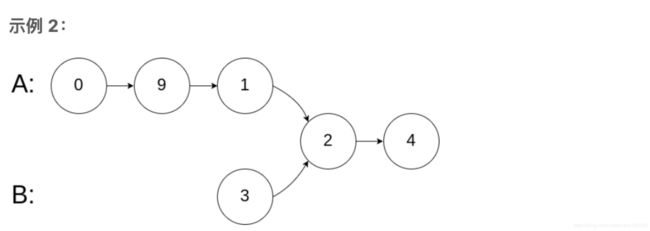
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Reference of the node with value = 2
输入解释:相交节点的值为 2 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
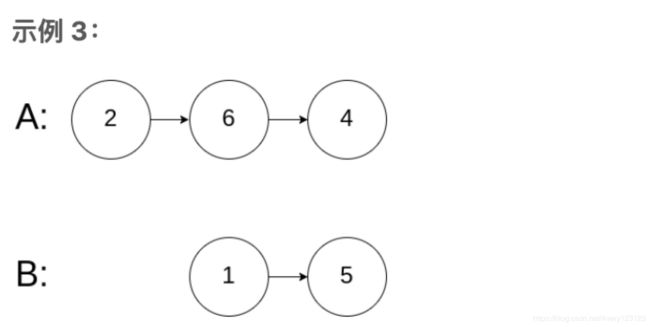
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
解释:这两个链表不相交,因此返回 null。
class LinkNode(object):
def __init__(self,x):
self.val = x
self.next = None
class Solution(object):
def getIntersectionNode(self,headA,headB):
p,q = headA,headB
countA = countB = 0
while p != None:
p = p.next
countA += 1
while q != None:
q = q.next
countB += 1
m,n = headA,headB
if countA > countB:
for i in range(countA-countB):
m = m.next
else:
for i in range(countB-countA):
n = n.next
while m != n:
m = m.next
n = n.next
return m
反转链表
反转一个单链表。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
进阶:
你可以迭代或递归地反转链表。你能否用两种方法解决这道题?
class Solution(object):
def reverseList(self,head):
if head is None:
return None
cur = head
pre = None
nxt = cur.next
while nxt:
cur.next = pre
pre = cur
cur = nxt
nxt = nxt.next
cur.next = pre
head = cur
return head
回文链表
请判断一个链表是否为回文链表。
示例 1:
输入: 1->2
输出: false
示例 2:
输入: 1->2->2->1
输出: true
进阶:
你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
class ListNode(object):
def __init__(self,x):
self.val = x
self.next = None
class Solution(object):
def isPalindrome(self,head):
if head is None or head.next is None:
return True
l = []
p = head
while p.next:
l.append(p.val)
p = p.next
l.append(p.val)
return l == l[::-1]
删除链表中的节点
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def deleteNode(self, node):
"""
:type node: ListNode
:rtype: void Do not return anything, modify node in-place instead.
"""
node.val = node.next.val
node.next = node.next.next
奇偶链表
给定一个单链表,把所有的奇数节点和偶数节点分别排在一起。请注意,这里的奇数节点和偶数节点指的是节点编号的奇偶性,而不是节点的值的奇偶性。
请尝试使用原地算法完成。你的算法的空间复杂度应为 O(1),时间复杂度应为 O(nodes),nodes 为节点总数。
示例 1:
输入: 1->2->3->4->5->NULL
输出: 1->3->5->2->4->NULL
示例 2:
输入: 2->1->3->5->6->4->7->NULL
输出: 2->3->6->7->1->5->4->NULL
说明:
应当保持奇数节点和偶数节点的相对顺序。
链表的第一个节点视为奇数节点,第二个节点视为偶数节点,以此类推。
class Solution(object):
def oddEvenList(self,head):
if not head or not head.next:
return head
odd_head = odd = head.next
even = head
while even and even.next and odd and odd.next:
even.next = even.next.next
even = even.next
odd.next = odd.next.next
odd = odd.next
even.next = odd_head
return head
哈希与映射
Python实现
Excel表列序号
给定一个Excel表格中的列名称,返回其相应的列序号。
例如,
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
示例 1:
输入: "A"
输出: 1
示例 2:
输入: "AB"
输出: 28
示例 3:
输入: "ZY"
输出: 701
class Solution(object):
def titleToNumber(self,s):
res = 0
for letter in s:
res = res *26+ord(letter)-ord('A')+1
return res
常数时间插入、删除和获取随机元素
设计一个支持在平均 时间复杂度 O(1) 下,执行以下操作的数据结构。
insert(val):当元素 val 不存在时,向集合中插入该项。
remove(val):元素 val 存在时,从集合中移除该项。
getRandom:随机返回现有集合中的一项。每个元素应该有相同的概率被返回。
示例 :
// 初始化一个空的集合。
RandomizedSet randomSet = new RandomizedSet();
// 向集合中插入 1 。返回 true 表示 1 被成功地插入。
randomSet.insert(1);
// 返回 false ,表示集合中不存在 2 。
randomSet.remove(2);
// 向集合中插入 2 。返回 true 。集合现在包含 [1,2] 。
randomSet.insert(2);
// getRandom 应随机返回 1 或 2 。
randomSet.getRandom();
// 从集合中移除 1 ,返回 true 。集合现在包含 [2] 。
randomSet.remove(1);
// 2 已在集合中,所以返回 false 。
randomSet.insert(2);
// 由于 2 是集合中唯一的数字,getRandom 总是返回 2 。
randomSet.getRandom();
import random
class RandomizedSet(object):
def __init__(self):
"""
Initialize your data structure here
"""
self.values = []
self.index = {}
def insert(self,val):
"""
Inserts a value to the set . Returns true if the set did not already contain the specified element.
:type val: int
:rtype: bool
"""
if val in self.index:
return False
self.values.append(val)
self.index[val] = len(self.values)-1
return True
def remove(self,val):
"""
Removes a value from the set. Returns true if the set contained the specified element.
:type val: int
:rtype: bool
"""
if val not in self.index:
return False
self.index[self.values[-1]] = self.index[val]
self.values[-1],self.values[self.index[val]] = self.values[self.index[val]],self.values[-1]
self.values.pop()
self.index.pop(val)
return True
def getRandom(self):
return self.values[random.randint(0,len(self.values)-1)]
四数相加 II
给定四个包含整数的数组列表 A , B , C , D ,计算有多少个元组 (i, j, k, l) ,使得 A[i] + B[j] + C[k] + D[l] = 0。
为了使问题简单化,所有的 A, B, C, D 具有相同的长度 N,且 0 ≤ N ≤ 500 。所有整数的范围在 -228 到 228 - 1 之间,最终结果不会超过 231 - 1 。
例如:
输入:
A = [ 1, 2]
B = [-2,-1]
C = [-1, 2]
D = [ 0, 2]
输出:
2
解释:
两个元组如下:
1. (0, 0, 0, 1) -> A[0] + B[0] + C[0] + D[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> A[1] + B[1] + C[0] + D[0] = 2 + (-1) + (-1) + 0 = 0
class Solution(object):
def fourSumCount(self, A, B, C, D):
"""
:type A: List[int]
:type B: List[int]
:type C: List[int]
:type D: List[int]
:rtype: int
"""
map1 = {}
res = 0
for a in A:
for b in B:
t = a + b
map1[t] = map1.get(t,0)+1
for c in C:
for d in D:
t = -c - d
if t in map1:
res += map1[t]
return res
树
Python实现
二叉搜索树中第K小的元素
class Solution(object):
def kthSmallest(self,root,k):
def inorderTraversal(root):
if root == None:
return []
res = []
res += inorderTraversal(root.left)
res.append(root.val)
res += inorderTraversal(root.right)
return res
return inorderTraversal(root)[k-1]
二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
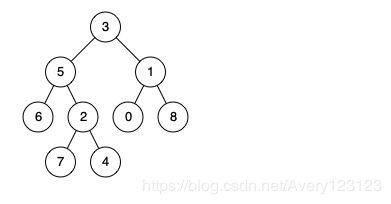
class TreeNodoe(object):
def __init__(self,x):
self.val = x
self.left = None
self.right = None
class Solution(object):
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
if not root or root == p or root == q:
return root
else:
left = self.lowestCommonAncestor(root.left,p,q)
right = self.lowestCommonAncestor(root.right,p,q)
if left and right:
return root
elif left:
return left
elif right:
return right
else:
return
二叉树的序列化与反序列化
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Codec:
def serialize(self, root):
"""Encodes a tree to a single string.
:type root: TreeNode
:rtype: str
"""
if not root:
return []
return_list = []
current_level = [root]
while len(current_level):
new_level = []
for current_node in current_level:
if current_node:
return_list.append(str(current_node.val))
new_level.append(current_node.left)
new_level.append(current_node.right)
else:
return_list.append(None)
current_level= new_level
return return_list
def deserialize(self, data):
"""Decodes your encoded data to tree.
:type data: str
:rtype: TreeNode
"""
if len(data) == 0:
return None
return_node = TreeNode(int(data[0]))
current_level = [return_node]
data = data[1:]
while len(current_level):
new_level = []
count = 0
for current_node in current_level:
if current_node:
count+=1
if not count:
break
new_level_data = data[:count*2]
data = data[count*2:]
count = 0
for current_node in current_level:
if current_node:
if new_level_data[count]:
current_node.left = TreeNode(int(new_level_data[count]))
count +=1
new_level.append(current_node.left)
if new_level_data[count]:
current_node.right = TreeNode(int(new_level_data[count]))
count += 1
new_level.append(current_node.right)
current_level = new_level
return return_node
# Your Codec object will be instantiated and called as such:
# codec = Codec()
# codec.deserialize(codec.serialize(root))
天际线问题
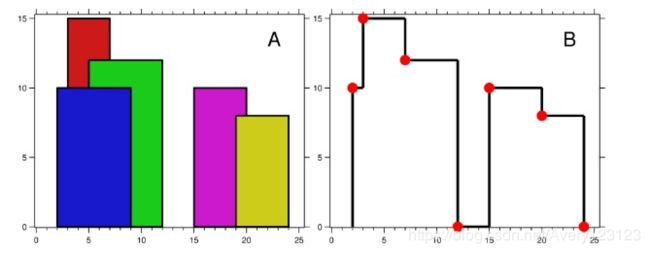
城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。现在,假设您获得了城市风光照片(图A)上显示的所有建筑物的位置和高度,请编写一个程序以输出由这些建筑物形成的天际线(图B)。
每个建筑物的几何信息用三元组 [Li,Ri,Hi] 表示,其中 Li 和 Ri 分别是第 i 座建筑物左右边缘的 x 坐标,Hi 是其高度。可以保证 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX 和 Ri - Li > 0。您可以假设所有建筑物都是在绝对平坦且高度为 0 的表面上的完美矩形。
例如,图A中所有建筑物的尺寸记录为:[ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] 。
输出是以 [ [x1,y1], [x2, y2], [x3, y3], … ] 格式的“关键点”(图B中的红点)的列表,它们唯一地定义了天际线。关键点是水平线段的左端点。请注意,最右侧建筑物的最后一个关键点仅用于标记天际线的终点,并始终为零高度。此外,任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。
例如,图B中的天际线应该表示为:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ]。
说明:
任何输入列表中的建筑物数量保证在 [0, 10000] 范围内。
输入列表已经按左 x 坐标 Li 进行升序排列。
输出列表必须按 x 位排序。
输出天际线中不得有连续的相同高度的水平线。例如 […[2 3], [4 5], [7 5], [11 5], [12 7]…] 是不正确的答案;三条高度为 5 的线应该在最终输出中合并为一个:[…[2 3], [4 5], [12 7], …]
解题思路:
采用最大堆。
将建筑物的左右边界存下来;
遍历所有边界,若其为某个建筑物的左边界,则将建筑物右边界和高度入堆;
若最大堆堆顶元素的右边界小于等于(因为若某个最大值是右边界,则最后存的不是该高度,而是除他之外最大的值,如例子中的 7)当前边界值,将其出堆;
取堆顶元素的建筑物高,若其不等于前一次的关键点,则说明该点与上一次的点不在一条水平线上,为一个“关键点”。
import heapq
class Solution(object):
def getSkyline(self,buildings):
borders = sorted([i[0] for i in buildings] + [i[1] for i in buildings])
index = 0
heap = []
res = [[0,0]]
for border in borders:
while index < len(buildings) and buildings[index][0] == border:
heapq.heappush(heap,[-buildings[index][2],buildings[index][1]])
index += 1
while heap and heap[0][1] <= border:
heapq.heappop(heap)
heigh = -heap[0][0] if heap else 0
if heigh != res[-1][1]:
res.append([border,heigh])
return res[1:]
排序与检索
Python实现
最大数
给定一组非负整数,重新排列它们的顺序使之组成一个最大的整数。
示例 1:
输入: [10,2]
输出: 210
示例 2:
输入: [3,30,34,5,9]
输出: 9534330
如果str(a)+str(b)>str(b)+str(a)那么a就比b更适合放在前面
例如‘9’ 和‘91’
str(‘9’)+str(‘91’)=’991‘
str(‘91’)+str(‘9’)=‘919’
‘991’>‘919’
所以9比91更适合放在前面
将数组所有数按照适合放在前面的程度排序再连起来即可
class Solution(object):
def largestNumber(self, nums):
"""
:type nums: List[int]
:rtype: str
"""
n = len(nums)
s = ''
for a in range(0,n-1):
for b in range(a+1,n):
if str(nums[a])+str(nums[b]) < str(nums[b]) + str(nums[a]):
nums[a],nums[b] = nums[b],nums[a]
for i in nums:
s = s+str(i)
if int(s) == 0:
return '0'
return s
摆动排序 II
给定一个无序的数组 nums,将它重新排列成 nums[0] < nums[1] > nums[2] < nums[3]… 的顺序。
示例 1:
输入: nums = [1, 5, 1, 1, 6, 4]
输出: 一个可能的答案是 [1, 4, 1, 5, 1, 6]
示例 2:
输入: nums = [1, 3, 2, 2, 3, 1]
输出: 一个可能的答案是 [2, 3, 1, 3, 1, 2]
说明:
你可以假设所有输入都会得到有效的结果。
进阶:
你能用 O(n) 时间复杂度和 / 或原地 O(1) 额外空间来实现吗
class Solution(object):
def wiggleSort(self,nums):
nums.sort()
half = len(nums[::2])
nums[::2],nums[1::2] = nums[:half][::-1],nums[half:][::-1]
return nums
寻找峰值
峰值元素是指其值大于左右相邻值的元素。
给定一个输入数组 nums,其中 nums[i] ≠ nums[i+1],找到峰值元素并返回其索引。
数组可能包含多个峰值,在这种情况下,返回任何一个峰值所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞。
示例 1:
输入: nums = [1,2,3,1]
输出: 2
解释: 3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入: nums = [1,2,1,3,5,6,4]
输出: 1 或 5
解释: 你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
在class Solution(object):
def findPeakElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
begain,end = 0,len(nums)-1
while begain < end:
mid = (begain+end)//2
if nums[mid] > nums[mid + 1]:
end = mid
else:
begain = mid + 1
return begain
寻找重复数
给定一个包含 n + 1 个整数的数组 nums,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。
示例 1:
输入: [1,3,4,2,2]
输出: 2
示例 2:
输入: [3,1,3,4,2]
输出: 3
说明:
不能更改原数组(假设数组是只读的)。
只能使用额外的 O(1) 的空间。
时间复杂度小于 O(n2) 。
数组中只有一个重复的数字,但它可能不止重复出现一次。
二分查找:
已知所有数字的范围是1-n, 就可以把left设为1, right 设为n,mid设为left 和right的中间值,
每次循环,用count记录一下有多少个小于等于mid的值,
如果count <= mid,就代表重复的数字应该不会落在mid左侧的区间内,于是更新left;
反之, 就更新right。
class Solution(object):
def findDuplicate(self,nums):
left,right = 1,len(nums)-1
while left<right:
mid = left+(right-left)/2
count = 0
for num in nums:
if num <= mid:
count += 1
if count <= mid:
left = mid+1
else:
right = mid
return left
count函数
class Solution(object):
def findDuplicate(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
for item in nums:
if nums.count(item) != 1:
return item
比较一下sum(nums)和sum(set(nums))和的差值,然后除以它们俩的长度差,就是那个重复的元素
class Solution(object):
def findDuplicate(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
return (sum(nums) - sum(set(nums)))/ (len(nums) - len(set(nums)))
计算右侧小于当前元素的个数
给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例:
输入: [5,2,6,1]
输出: [2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1).
2 的右侧仅有 1 个更小的元素 (1).
6 的右侧有 1 个更小的元素 (1).
1 的右侧有 0 个更小的元素.
暴力法:(超出时间限制)
class Solution(object):
def countSmaller(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
lens = len(nums)
res = [0]*lens
i = lens-2
while i >= 0:
t = 0
j = lens-1
while j>i:
if nums[j] < nums[i]:
t +=1
j -= 1
res[i] = t
i -= 1
return res
插入排序(超出时间时间限制):
class Solution2(object):
def countSmaller(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
lens = len(nums)
if lens == 0:
return []
res = [0]*lens
temp = [-1]*lens#在temp数组中找到第一个大于等于待插入元素的索引
temp[0] = nums[lens-1]
res[lens-1] = 0
end = 1#指向即将写入的那个元素
i = lens-2
while i >= 0 :
if nums[i] > temp[end-1]:
temp[end] = nums[i]
res[i] = end
else:#插入排序
j = end
tempVal = nums[i]
while j > 0 and temp[j-1] >= tempVal:
temp[j] = temp[j-1]
j -= 1
temp[j] = tempVal
res[i] = j
end+=1
i+=1
result = []
for i in range(lens):
result.append(res[i])
return result
动态规划
Python实现
打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
class Solution(object):
def rob(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
last = 0
now = 0
for i in nums:
last,now = now,max(last+i,now)
return now
完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
示例 2:
输入: n = 13
输出: 2
解释: 13 = 4 + 9.
动态规划
class Solution:
def numSquares(self,n):
"""
:type n: int
:rtype: int
"""
dp = [0]*(n+1)#默认初始化为0
for i in range(1,n+1):
dp[i] = i #z最坏情况每次都是+1
j = 1
while i >= j*j:
dp[i] = min(dp[i],dp[i-j*j]+1)
j +=1
return dp[n]
队列的方法:
class Solution2:
def numSquares(self,n):
"""
:type n: int
:rtype: int
"""
q = []
q.append([n,0])
visted = [False for _ in range(n+1)]
visted[n] = True
while(len(q) != 0):
num,step = q.pop(0)
i = 1
tNum = num -i*i
while tNum >= 0:
if tNum == 0:
return step+1
if not visted[tNum]:
q.append((tNum,step+1))
visted[tNum] = True
i += 1
tNum = num -i*i
最长上升子序列
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?、
class Solution(object):
def lengthOfLIS(self,nums):
if nums == []:
return 0
N = len(nums)
dp = [1]*N
for i in range(N-1):
for j in range(0,i+1):
if nums[i+1] > nums[j]:
dp[i+1] = max(dp[i+1],dp[j]+1)
return max(dp)
零钱兑换
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1
说明:
你可以认为每种硬币的数量是无限的。
class Solution(object):
def coinChange(self,coins,amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
dp = [-1]*(amount+1)
dp[0] = 0
for i in range(1,amount+1):
for j in range(len(coins)):
if i >= coins[j] and dp[i-coins[j]] != -1:
if dp[i] == -1 or dp[i] > dp[i-coins[j]] != -1:
dp[i] = dp[i - coins[j]]+1
return dp[amount]
最长连续序列
给定一个未排序的整数数组,找出最长连续序列的长度。
要求算法的时间复杂度为 O(n)。
示例:
输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。
class Solution(object):
def longestConsecutive(self,nums):
"""
:type nums: List[int]
:rtype: int
"""
nums = set(nums)
res = 0
for i in nums:
if (i-1) not in nums:
y = i + 1
while y in nums:
y += 1
res = max(res,y-i)
return res
二叉树中的最大路径和
给定一个非空二叉树,返回其最大路径和。
本题中,路径被定义为一条从树中任意节点出发,达到任意节点的序列。该路径至少包含一个节点,且不一定经过根节点。
示例 1:
输入: [1,2,3]
1
/ \
2 3
输出: 6
示例 2:
输入: [-10,9,20,null,null,15,7]
-10
/ \
9 20
/ \
15 7
输出: 42
class Solution(object):
def __init__(self):
self.result = float('-inf')
def maxPathSum(self,root):
"""
:type root: TreeNode
:rtype: int
"""
if root == None:
return 0
self.getMax(root)
return self.result
def getMax(self,root):
"""辅助函数"""
#如果当前节点为空就表示包含当前当前的最大路径为0
if root == None:
return 0
#递归的计算当前节点的左子树和右子树能提供的最大路径和。如果为负就置为0(相当于从头开始)
left = max(0,self.getMax(root.left))
right = max(0,self.getMax(root.right))
# 注意:最长的路径肯定是属于从一端的最左侧到这端的最右侧的一部分
# 每计算一次左右子树的最大值,就更新当前的result
self.result = max(self.result,left+right+root.val)
#回溯到父节点,最大路径就只能包含左右两个子树中的一个
return max(left,right) + root.val
优化一下:
class Solution2(object):
def maxPathSum(self,root):
self.curr_max = float('-inf')
def getMax(root):
if root == None:
return 0
left = max(0,getMax(root.left))
right = max(0,getMax(root.right))
self.curr_max = max(self.curr_max,left+right+root.val)
return max(left,right) + root.val
getMax(root)
return self.curr_max
矩阵中的最长递增路径
给定一个整数矩阵,找出最长递增路径的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你不能在对角线方向上移动或移动到边界外(即不允许环绕)。
示例 1:
输入: nums =
[
[9,9,4],
[6,6,8],
[2,1,1]
]
输出: 4
解释: 最长递增路径为 [1, 2, 6, 9]。
示例 2:
输入: nums =
[
[3,4,5],
[3,2,6],
[2,2,1]
]
输出: 4
解释: 最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
**分析:**假设最长路径终点的是[i][j],则其最长路径值为nums1[i][j],则nums1[i][j]等于它上下左右四个数中,比它小的数中最长路径值最大的那一个+1
因此,我们可以从矩阵的最小值出发,其最长路径值为1,然后计算第二小的数的最长路径值,以此类推
至少有K个重复字符的最长子串
找到给定字符串(由小写字符组成)中的最长子串 T , 要求 T 中的每一字符出现次数都不少于 k 。输出 T 的长度。
示例 1:
输入:
s = "aaabb", k = 3
输出:
3
最长子串为 “aaa” ,其中 ‘a’ 重复了 3 次。
示例 2:
输入:
s = “ababbc”, k = 2
输出:
5
最长子串为 “ababb” ,其中 ‘a’ 重复了 2 次, ‘b’ 重复了 3 次。
图论
Python实现
岛屿数量
给定一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
示例 1:
输入:
11110
11010
11000
00000
输出: 1
示例 2:
输入:
11000
11000
00100
00011
输出: 3
递归+dfs
class Solution(object):
def numIslands(self,grid):
"""
:type grid: List[List[str]]
:rtype: int
"""
count = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == '1':
self.dfs(grid,i,j)
count += 1
return count
def dfs(self,grid,i,j):
if i < 0 or j < 0 or i >= len(grid) or j >=len(grid[0]) or grid[i][j] != '1':
return
grid[i][j] = '#'
self.dfs(grid,i+1,j)
self.dfs(grid,i-1,j)
self.dfs(grid,i,j+1)
self.dfs(grid,i,j-1)
课程表
现在你总共有 n 门课需要选,记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件,判断是否可能完成所有课程的学习?
示例 1:
输入: 2, [[1,0]]
输出: true
解释: 总共有 2 门课程。学习课程 1 之前,你需要完成课程 0。所以这是可能的。
示例 2:
输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0;并且学习课程 0 之前,你还应先完成课程 1。这是不可能的。
说明:
输入的先决条件是由边缘列表表示的图形,而不是邻接矩阵。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。
提示:
这个问题相当于查找一个循环是否存在于有向图中。如果存在循环,则不存在拓扑排序,因此不可能选取所有课程进行学习。
通过 DFS 进行拓扑排序 - 一个关于Coursera的精彩视频教程(21分钟),介绍拓扑排序的基本概念。
拓扑排序也可以通过 BFS 完成。
方法1:
每一次都删除没有入度的节点、看是否能删完
class Solution(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
d = {}
for a,b in prerequisites:
d[a] = d[a] + [b] if a in d else [b]
courses = list(range(numCourses))
t = len(courses)+1
#没有变化就跳出
while len(courses) < t:
t = len(courses)
for c in courses:
#没有先修课的课程,就是没有入度的节点
if c not in d:
#学完就删除
courses.remove(c)
for x in list(d.keys()):
if c in d[x]:
d[x].remove(c)
#当x课的先修课程都学完了,就从字典中删除它,它就成了没有入度的节点了
if d[x] == []:
d.pop(x)
return courses == []
方法2:
找环,若有环就学不完
class Solution2(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
graph = [[] for _ in range(numCourses)]
visited = [0]*numCourses
for k,v in prerequisites:
graph[k].append(v)
def dfs(i):
if visited[i] == 1:
return True
if visited[i] == -1:
return False
visited[i] = -1
for pre in graph[i]:
if not dfs(pre):
return False
visited[i] = 1
return True
for i in range(numCourses):
if not dfs(i):
return False
return True
课程表 II
现在你总共有 n 门课需要选,记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件,返回你为了学完所有课程所安排的学习顺序。
可能会有多个正确的顺序,你只要返回一种就可以了。如果不可能完成所有课程,返回一个空数组。
示例 1:
输入: 2, [[1,0]]
输出: [0,1]
解释: 总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
示例 2:
输入: 4, [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
说明:
输入的先决条件是由边缘列表表示的图形,而不是邻接矩阵。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。
提示:
这个问题相当于查找一个循环是否存在于有向图中。如果存在循环,则不存在拓扑排序,因此不可能选取所有课程进行学习。
通过 DFS 进行拓扑排序 - 一个关于Coursera的精彩视频教程(21分钟),介绍拓扑排序的基本概念。
拓扑排序也可以通过 BFS 完成。
解题思路
遍历输入中的所有边,创建邻接表,out_degree[i]存储所有把第i节课作为预备课程的课,并用in_degree[i]存储结点i的入度。
将所有入度为0的边加入 res
执行以下操作直到 res中不再增加元素:
遍历res中的元素。不妨称为 N。对 N的所有邻接节点, 将其入度减去1。若任意结点的入度变为0,将其加入res。
class Solution(object):
def findOrder(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: List[int]
"""
in_degree = [0]*numCourses
out_degree = [[] for _ in range(numCourses)]
for course ,pre in prerequisites:
in_degree[course] += 1
out_degree[pre].append(course)
res = []
for i in range(numCourses):
if in_degree[i] == 0:
res.append(i)
l = 0
while l != len(res):
x = res[l]
l += 1
for i in out_degree[x]:
in_degree[i] -= 1
if in_degree[i] == 0:
res.append(i)
return res if l == numCourses else []
单词接龙
给定两个单词(beginWord 和 endWord)和一个字典,找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则:
每次转换只能改变一个字母。
转换过程中的中间单词必须是字典中的单词。
说明:
如果不存在这样的转换序列,返回 0。
所有单词具有相同的长度。
所有单词只由小写字母组成。
字典中不存在重复的单词。
你可以假设 beginWord 和 endWord 是非空的,且二者不相同。
示例 1:
输入:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
输出: 5
解释: 一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog",
返回它的长度 5。
示例 2:
输入:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]
输出: 0
解释: endWord "cog" 不在字典中,所以无法进行转换。
思路:本题需要用到广度优先搜索(BFS,broad first search)。
class Solution(object):
# 本题采用广度遍历方法
def ladderLength(self, beginWord, endWord, wordList):
"""
:type beginWord: str
:type endWord: str
:type wordList: List[str]
:rtype: int
"""
# 首先给wordList列表中单词去重
word_set = set(wordList)
# 定义当前层的单词集合为beginWord
cur_word = [beginWord]
# 定义下一层的单词集合
next_word = []
# 定义从 beginWord 到 endWord 的最短转换序列的长度
depth = 1
while cur_word:
for word in cur_word:
# 如果endWord出现在当前层的cur_word单词集合中,则立即返回该深度
if word == endWord:
return depth
for index in range(len(word)):
for indice in "abcdefghijklmnopqrstuvwxyz":
new_word = word[:index] + indice + word[index + 1:]
if new_word in word_set:
word_set.remove(new_word)
next_word.append(new_word)
# 如果endWord未出现在当前层的cur_word单词集合中,则深度+1
depth += 1
cur_word = next_word
next_word = []
return 0
if __name__ == "__main__":
beginWord = "hit"
endWord = "cog"
wordList = ["hot", "dot", "dog", "lot", "log", "cog"]
sequence_length = Solution().ladderLength(beginWord, endWord, wordList)
print(sequence_length)
单词接龙 II
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4
数学问题
直线上最多的点数
给定一个二维平面,平面上有 n 个点,求最多有多少个点在同一条直线上。
示例 1:
输入: [[1,1],[2,2],[3,3]]
输出: 3
解释:
^
|
| o
| o
| o
+------------->
0 1 2 3 4
示例 2:
输入: [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出: 4
解释:
^
|
| o
| o o
| o
| o o
+------------------->
0 1 2 3 4 5 6
穷举,算出每个点和其他各个点的斜率(若两个点和同一个点的斜率相同,那么这三个点在同一条直线上),计算不同斜率点的个数(别忘了把当前点加上),还要注意和当前点重合的,以及斜率为无穷的。
import numpy as np
class Solution(object):
def maxPoints(self, points):
"""
:type points: List[List[int]]
:rtype: int
"""
n = len(points)
slope_map = {}
res = 0
for i in range(n):
slope_map.clear()
same,vertical = 1,0
slope_max = 0
for j in range(i+1,n):
dx = points[i][0] - points[j][0]
dy = points[i][1] - points[j][1]
#同一个点
if dx == dy == 0:
same += 1
#斜率无穷大(垂直)
elif dx == 0:
vertical += 1
#有斜率的点
else:
slope = (dy * np.longdouble(1)) / dx
#特殊处理
slope_map[slope] = slope_map.get(slope,0) + 1
slope_max = max(slope_max,slope_map[slope])
res = max(res,max(slope_max,vertical)+same)
return res
分数到小数
给定两个整数,分别表示分数的分子 numerator 和分母 denominator,以字符串形式返回小数。
如果小数部分为循环小数,则将循环的部分括在括号内。
示例 1:
输入: numerator = 1, denominator = 2
输出: "0.5"
示例 2:
输入: numerator = 2, denominator = 1
输出: "2"
示例 3:
输入: numerator = 2, denominator = 3
输出: "0.(6)"
class Solution(object):
def fractionToDecimal(self, numerator, denominator):
"""
:type numerator: int
:type denominator: int
:rtype: str
"""
if numerator == 0:
return '0'
elif denominator == 0:
return ''
else:
isNegative = (numerator < 0) ^ (denominator < 0)
numerator = abs(numerator)
denominator = abs(denominator)
res = ''
res += '-' if isNegative else ''
res += str(numerator//denominator)
numerator %= denominator
if numerator == 0:
return res
else:
res +='.'
dic = {}
while numerator:
if numerator in dic:
start = dic[numerator]
end = len(res)
res = res[:start] + '(' + res[start:end] + ')'
return res
dic[numerator] = len(res)
res += str(numerator*10//denominator)
numerator = numerator*10%denominator
return res
阶乘后的零
给定一个整数 n,返回 n! 结果尾数中零的数量。
示例 1:
输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。
示例 2:
输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.
说明: 你算法的时间复杂度应为 O(log n)
class Solution(object):
def trailingZeroes(self,n):
r = 0
while n >= 5:
n = n//5
r += n
return r
颠倒二进制位
颠倒给定的 32 位无符号整数的二进制位。
示例 1:
输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596,
因此返回 964176192,其二进制表示形式为 00111001011110000010100101000000。
示例 2:
输入:11111111111111111111111111111101
输出:10111111111111111111111111111111
解释:输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293,
因此返回 3221225471 其二进制表示形式为 10101111110010110010011101101001。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在上面的 示例 2 中,输入表示有符号整数 -3,输出表示有符号整数 -1073741825。
进阶:
如果多次调用这个函数,你将如何优化你的算法?
class Solution(object):
def reverseBits(self,n):
one = 1
res = 0
for i in range(32):
res = (res<<1)+(n&one)
n = n >> 1
return res
位1的个数
编写一个函数,输入是一个无符号整数,返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量)。
示例 1:
输入:00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
示例 2:
输入:00000000000000000000000010000000
输出:1
解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。
示例 3:
输入:11111111111111111111111111111101
输出:31
解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。
class Solution(object):
def hammingWeight(self,n):
if n == 0:
return 0
sum = 0
while n >0:
sum += n&1
#相当于依次右移,然后计算下一位的值&1
n = n >> 1
return sum
计数质数
统计所有小于非负整数 n 的质数的数量。
示例:
输入: 10
输出: 4
解释: 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
class Solution(object):
def countPrimes(self,n):
"""
:type n: int
:rtype: int
"""
a = [1]*n
count = 0
for i in range(2,n):
if a[i] == 1:
count += 1
j = 1
while i * j<n:
a[i*j] = 0
j+=1
return count
缺失数字
给定一个包含 0, 1, 2, …, n 中 n 个数的序列,找出 0 … n 中没有出现在序列中的那个数。
示例 1:
输入: [3,0,1]
输出: 2
示例 2:
输入: [9,6,4,2,3,5,7,0,1]
输出: 8
说明:
你的算法应具有线性时间复杂度。你能否仅使用额外常数空间来实现?
class Solution(object):
def missingNumber(self,nums):
"""
:type nums: List[int]
:rtype: int
"""
bit = 0
for i,j in enumerate(nums):
bit ^= i ^ j
return bit^len(nums)
3的幂
class Solution(object):
def isPowerOfThree(self,n):
"""
:type n: int
:rtype: bool
"""
while n > 0:
if n % 3 == 0:
n /= 3
else:
break
return True if n == 1 else False