本次数据集来自于天池新人赛
-
赛题描述:
火力发电的基本原理是:燃料在燃烧时加热水生成蒸汽,蒸汽压力推动汽轮机旋转,然后汽轮机带动发电机旋转,产生电能。在这一系列的能量转化中,影响发电效率的核心是锅炉的燃烧效率,即燃料燃烧加热水产生高温高压蒸汽。锅炉的燃烧效率的影响因素很多,包括锅炉的可调参数,如燃烧给量,一二次风,引风,返料风,给水水量;以及锅炉的工况,比如锅炉床温、床压,炉膛温度、压力,过热器的温度等
数据分成训练数据(train.txt)和测试数据(test.txt),其中字段”V0”-“V37”,这38个字段是作为特征变量,”target”作为目标变量。选手利用训练数据训练出模型,预测测试数据的目标变量,排名结果依据预测结果的MSE(mean square error)。
经脱敏后的锅炉传感器采集的数据(采集频率是分钟级别),根据锅炉的工况,预测产生的蒸汽量。
-
线性回归
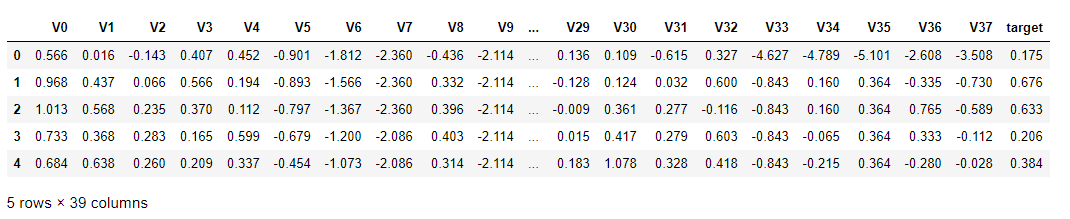
本次数据采用线性回归模型进行预测,首先查看一下数据
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import statsmodels.api as sm
df = pd.read_table('zhengqi_train.txt')
df.head()
查看数据的缺失情况,经确认并没有缺失值
df.isnull().sum()
本次用的是statsmodels模块,所以需要提取所有的字段。由于字段过多,我构造了一个函数:
lst = [] #构造自变量特征名,方便建模使用
for i in range(38):
lst.append('V'+str(i))
x_name = '+'.join(lst)
print(x_name)
输出结果是一个字符串V0+V1+V2+V3+V4+V5+V6+V7+V8+V9+V10+V11+V12+V13+V14+V15+V16+V17+V18+V19+V20+V21+V22+V23+V24+V25+V26+V27+V28+V29+V30+V31+V32+V33+V34+V35+V36+V37
这样就可以方便的创建线性回归模型了。
train, test = train_test_split(df, test_size=0.25, random_state=66) # 拆分训练集和测试集
model = sm.formula.ols('target~'+ x_name, data=train).fit()
model.params # 偏回归系数
模型的检验
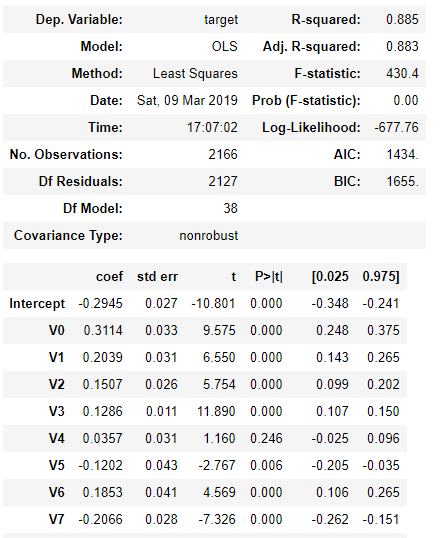
通过model.summary()可以得到模型的一些信息(部分截图如下)
- R-squared:判决系数R平方,用来衡量自变量对因变量解释程度。
- F-statistic:模型的F统计量,用来检验模型的显著性。
- P>|t|:每个t统计量对应的概率值p,用来检验回归系数的显著性。一般p值小于0.05,说明此变量是因变量的影响因素。
线性相关性检验
corr = train.drop('target', axis=1).corrwith(train.target)
corr = corr[np.abs(corr) >= 0.5]
这里只留取了先关系数大于等于0.5的变量,再综合上面的t检验,最终确定下1-v12,v14,v16,v17,v24,v27,v31,v33,v37作为模型的自变量,再根据这些变量建立新的模型
model2 = sm.formula.ols('target~V1+V2+V3+V4+V5+V6+V7+V8+V9+V10+V11+V12+V14+V16+V17+V24+V27+V31+V33+V37', data=train).fit()
pred = model2.predict(exog=test.ix[:,['V1','V2','V3','V4','V5','V6','V7','V8','V9','V10','V11','V12','V14','V16','V17','V24','V27','V31','V33','V37']])
MSE = np.sum((test.target-pred) ** 2)/test.shape[0]
MSE
比赛是根据MSE评分的,这里我计算得出本次模型的MSE为0.12064232053155005
目测这个结果在排行榜中排到了90多名。