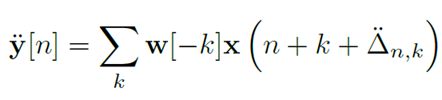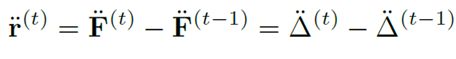Deformable Conv及其变体
文章列表：
Active Convolution: Learning the Shape of Convolution for Image Classification
这篇文章首先将卷积进行参数的拓展，之前都是直接学习权重就是了。之前的卷积都是fixed的采样。比如3*3，就是采样与window中心点相对位置一样的9个点。即：
Y = W ∗ X + b Y=W*X+b Y=W∗X+b
y m , n = ∑ c ∑ i , j w c , i , j ⋅ x c , m + i , n + j + b y_{m,n}=\sum_{c}\sum_{i,j}w_{c,i,j}\cdot x_{c,m+i,n+j}+b ym,n=c∑i,j∑wc,i,j⋅xc,m+i,n+j+b
如果将 X X X进行修改：
Y = W ∗ X θ p + b Y=W*X_{\theta_{p}}+b Y=W∗Xθp+b
y m , n = ∑ c ∑ k w c , k ⋅ x c , m + α k , n + β k + b y_{m,n}=\sum_{c}\sum_{k}w_{c,k}\cdot x_{c,m+ \alpha _{k}, n+\beta_{k}}+b ym,n=c∑k∑wc,k⋅xc,m+αk,n+βk+b
θ p = ( − 1 , − 1 ) , ( 0 , − 1 ) , ( 1 , − 1 ) , . . . , ( 1 , 1 ) \theta_{p}={(-1,-1), (0,-1),(1,-1),..., (1,1)} θp=(−1,−1),(0,−1),(1,−1),...,(1,1)
p k = ( α k , β k ) ∈ R 2 p_{k}=(\alpha_k, \beta_k)\in R^2 pk=(αk,βk)∈R2
也就是说，这里对 K K K（一般是3*3=9个之类的）个参数，每个参数都加了一个offset ( α k , β k ) (\alpha_{k}, \beta_{k}) (αk,βk).
也就是说，这就是所谓的ACU（active convolution unit）。新增的卷积参数是 2 ∗ K 2*K 2∗K.
注意：这里的offset是across channels，也是across spatial dimension的！也就是说，每个通道的offset都是一样的，同时spatial 上的每个点为中心的2*9个offset，都是一样的。
其实我们知道，
- 每个通道共享offset是肯定合理的。首先，同一个点的位置，不同通道只是提取了该点为中心的local的不同类型的feature，但是这些feature都的组合都是表达这个local的同一pixel level的信息。因此，不应该逐个通道采用不同的offset。
- 但是，across spatial dimension进行共享offset就肯定不是很科学。显然，如果让卷积自动根据物体的形状进行变形，那肯定是要对每个spatial点，都要相应的学习一个最优的offest。才能对输入图片的每个位置，adaptive地采样最佳的feature点，从而完成相应的任务。这个在Detection中就特别合理。
##计算方式
前向，插值。反向不贴图了，浪费空间。
一个比较重要的是，这个插值其实是对位置进行插值的，对位置插值后，得到4个格点的权重系数，然后加权平均4个格点的像素，进而实现前向。
Deformable Convolution Networks
刚才我们在第一篇论文讲了，这个offests进行across spatial dimension共享完全不合理啊。特别是对detection等任务。这些任务对物体的形状是很敏感的。
那么，我们得让这个offsets是对每个spatial点，都能有 2 ∗ N 2*N 2∗N个参数。注意，这个 N N N就是上篇提到的 K K K，一般是 3 ∗ 3 3*3 3∗3之类的。
我们算算，假设输入的feature的spatial size是 H ∗ W H*W H∗W, emm，我们应该要预测 H ∗ W ∗ ( 2 ∗ N ) H*W*(2*N) H∗W∗(2∗N)个参数。其中 N = 3 ∗ 3 ， 5 ∗ 5 , . . . N=3*3，5*5,... N=3∗3，5∗5,...
那么，显然，是将feature，通过一些卷积，然后生成通道数为 2 N 2N 2N的新的feature，这个新的feature的大小为 ( 2 N ) ∗ H ∗ W (2N)*H*W (2N)∗H∗W. 这些feature的值就是我们原先feature的offests。
如下图：
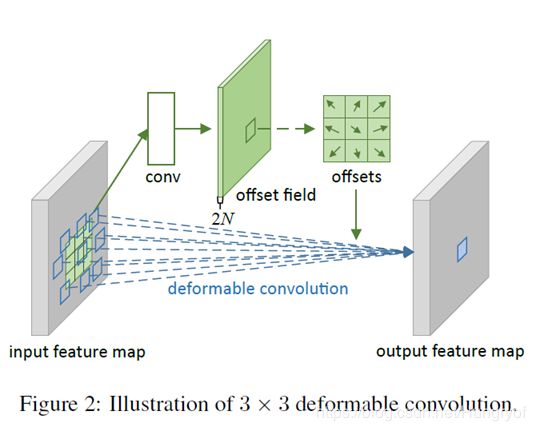
普通卷积
y ( p 0 ) = ∑ p n ∈ R w ( p n ⋅ x ( p 0 + p n ) y(p_0)=\sum_{p_n\in R} \mathbf{w}({\mathbf{p}_n}\cdot \mathbf{x}(\mathbf{p}_0+\mathbf{p}_n) y(p0)=pn∈R∑w(pn⋅x(p0+pn)
deformable 卷积
y ( p 0 ) = ∑ p n ∈ R w ( p n ⋅ x ( p 0 + p n + Δ p n ) y(p_0)=\sum_{p_n\in R} \mathbf{w}({\mathbf{p}_n}\cdot \mathbf{x}(\mathbf{p}_0+\mathbf{p}_n+\Delta\mathbf{p}_{n}) y(p0)=pn∈R∑w(pn⋅x(p0+pn+Δpn)
行吧，下面的公式贴图吧~
其实就是对 p p p,找到它的临近4个点，然后插值得到。具体算法和上篇论文差不多。
Deformable ROIPooling
不做Detection之类的任务可以不用看。太task-specific了。
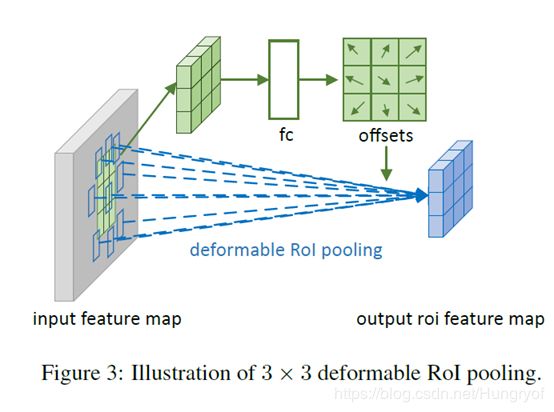
普通ROIPooling
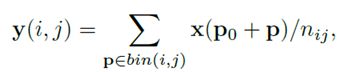
Deformable ROIPooling
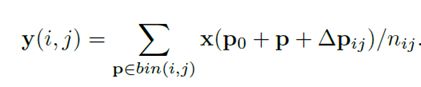
其实类似的，deform conv是对采样点加offsets，自然defrom ROIPooling自然是对bins加offsets操作了。
可视化
我们可以看到，一个点其实是由前一层的9个点采样加权得到，那么这里显示了3层。绿点表示pixel 上的一个点，这个点在前面的第三层其实是由 9 3 = 729 9^3=729 93=729个点采样加权得到。发现，这写采样点，基本可以覆盖物体的形状。如果是背景的话，也是基本分布在背景区域。
下面是deformable ROIPooling的，可以看到，这些狂基本能移动到bbox的物体内部，从而忽略多余的背景部分。
Deformable conv到底学了什么？？
注意：它不是学习了offsets！而是学习了根据不同特征，提取该特征所需要的相应的offsets的能力！！！
这个能力其实就是，上面分支的“conv”的卷积层的参数！
这就是deformable的强大之处，比如，一条狗站着和趴着，当deformable卷积学习时，看到了趴着的狗，上面的分支的conv可以将这个feature作为输入，然后输出“趴着的狗”所需要的offsets，这时候的offsets基本是让下面的分支的卷积的采样点呈现“扁平框”的样式。当然了，如果是看着了“站着的狗”，offsets就会让下面分支的卷积的采样点呈现“更加四四方方点了”（哈哈，狗并不是一个正方形好不好~~），
Deformable ConvNets v2: More Deformable, Better Results
这个没啥好说的啊，简单来说，就是之前v1版本，你要拓展，咋拓展，其实，你都加了offset了，认为每个spatial点的offset都要能学出了，显然剩下的最容易想到的就是加权重了。
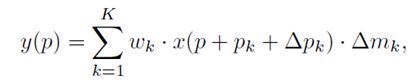
论文的两个创新点：
那么，表现就是，上面的一个分支，不再只用一个conv了，用多个conv来提升根据不同特征预测相应的offsets的能力。
其次是，我们需要的参数不再是 ( 2 K ) ∗ H ∗ W (2K)*H*W (2K)∗H∗W了（真的烦，这里又把N写成了K），因为加了一个权重，所以上面的一个分支出来的offsets的通道应该是 3 K 3K 3K。多的一个 K K K的通道就是权重，送入sigmoid，让其为0-1之间就行。
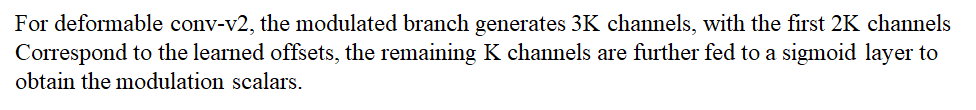
结果不贴了，反正有提升就行。
Locally-Consistent Deformable Convolution Networks for Fine-Grained Action Detection
因为细粒度动作识别，基本都是temporal 信息与spatial信息，用一个module融合，再将信息输入到类似LSTM中。再进行分类。
提取temporal信息基本都是用光流进行的。光流网络难以训练，而且，提取spatial信息需要一个网络，光流又是另一个网络，就造成参数复杂。那么对于细粒度动作识别这个任务，怎么直接从一个提取spatial信息的网络中提取temproal信息呢。
就是，文中认为，如果用deformable卷积，那么两帧之间的offsets的差值就是光流。
因为，如果deformable conv用于动作识别中，因为这个任务的视频基本动作发生者是不会改变的。那么这个deformable如果学习得比较好，那么相当于一种检测关键点的功能。那么显然，这些关键点的变化，就是光流。
我们可以看到，这个offsets是2个自由度的。
动作信息
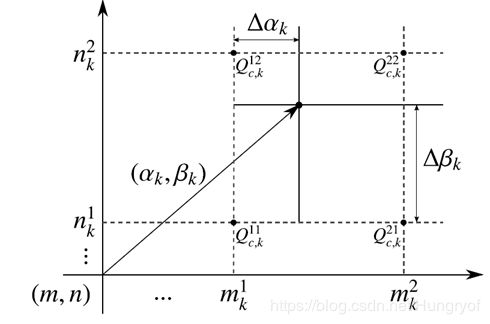
对于动作识别这个特殊的任务，由于光流的话，每个点的光流是确定的。但是，但是你看下面这张图：
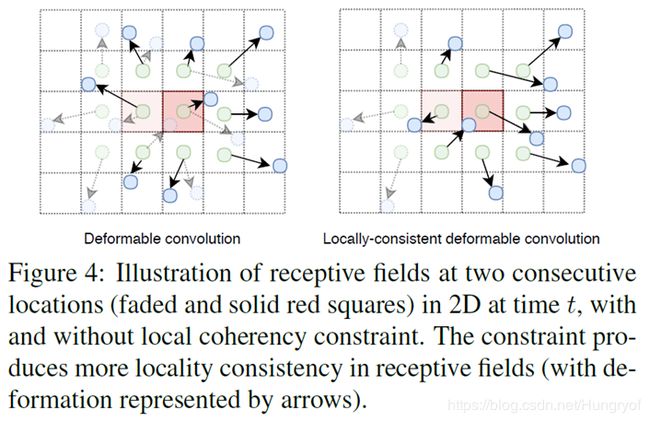虚线框是代表第一个位置，那么虚线的绿色点代表第一次的普通卷积的采样点。那么如果假设第一次的位置的deformable使得这个位置变成了虚线的蓝色点。
但是，当我们把卷积核window center往右边移动一个位置，这时候。我们发现，第一行的绿色点的第二点。你发现，这个绿点，针对第一个位置和第二个位置分别有一个offset。那么在 t + 1 t+1 t+1帧时，这个位置又会有2个offset，那么一个点就会又多个offsets！光流咋算，完全没法弄啊。
这时候，我们针对这个任务肯定要让offset的表示不再以window center为中心的了！而是以其本身的位置点为中心。也就是说，一个点的位置，就一个offset！而不是之前一个点的位置，根据其属于的windows center不同，有多个offsets（比如3*3的，一个点有9的offsets）
这时候，我么看第二个图，不解释了。你看得懂的。
那么，对于这个local-consistent的卷积，形式就是下面：
对于，local-consistent 卷积，由于每个点都是一个offset，不会根据window center的中心而改变。那么这个offset其实可以相当于直接认为，是先对feature进行shift操作，然后再进行常规卷积。
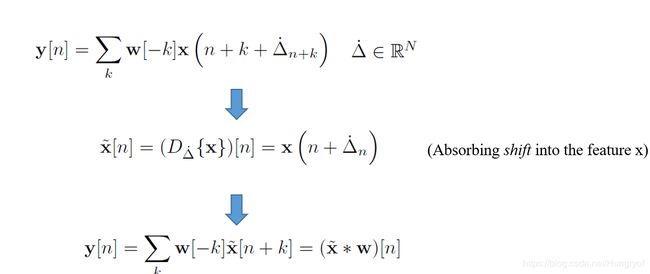话说回来，其实自定义卷积操作，基本是要转换成常规卷积来弄的。一个方法就是，先将feature进行一下特定操作。再用常规卷积来卷。比如对于partial conv等等吧。看着很高端，其实很简单。
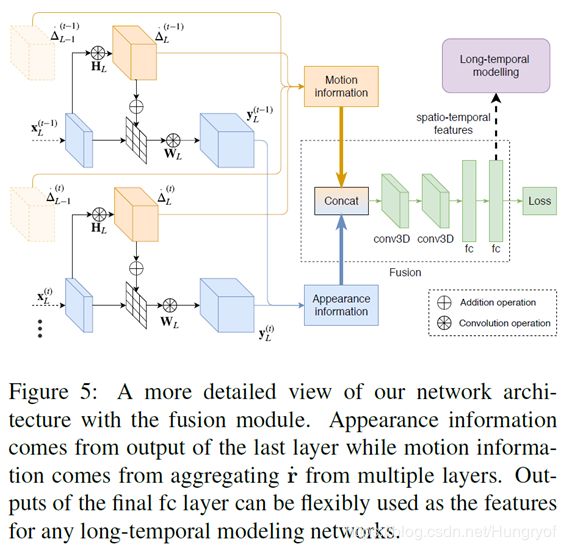
下面是这个任务的网络图。解释略。
