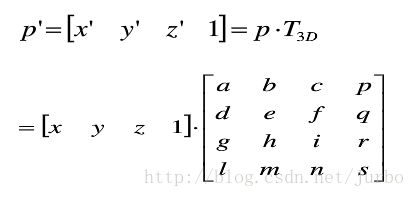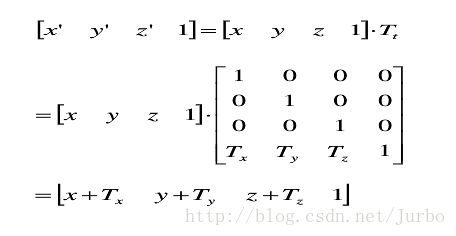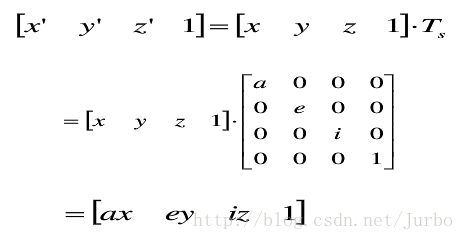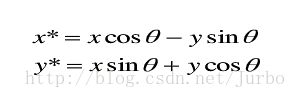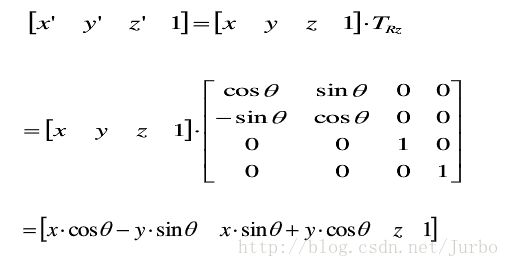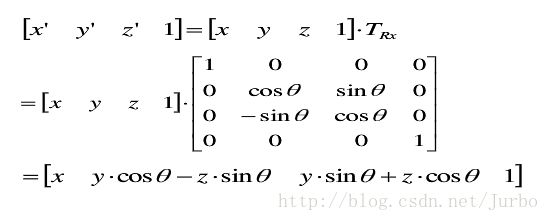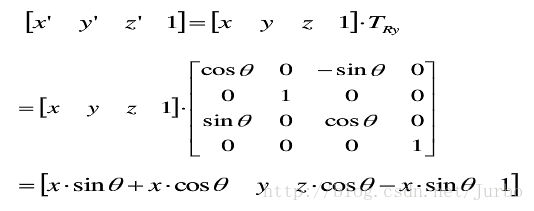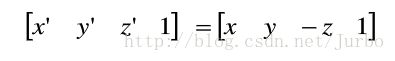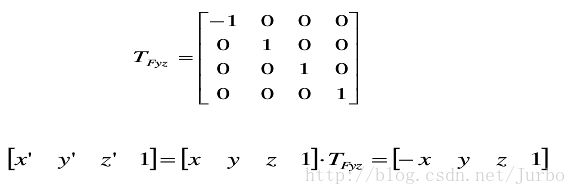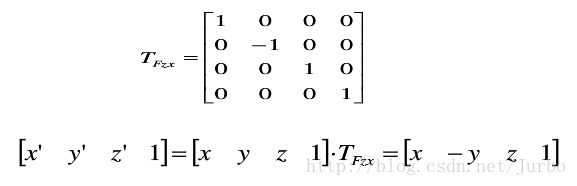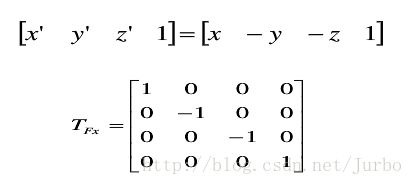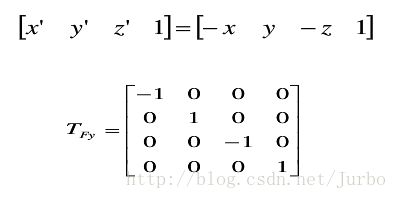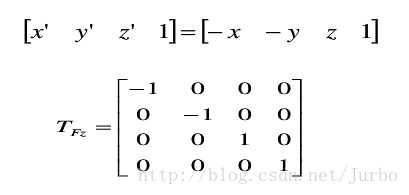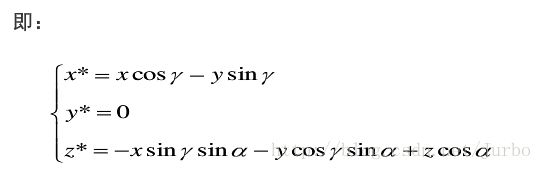计算机图形学 学习笔记（八）：三维图形变换：三维几何变换，投影变换（平行/ 透视 投影）

接上文 计算机图形学 学习笔记（七）：二维图形变换：平移，比例，旋转，坐标变换等

---

通过三维图形变换，可由简单图形得到复杂图形，三维图形变化则分为三维几何变换和投影变换。

6.1 三维图形几何变换

三维物体的几何变换是在二维方法基础上增加了对 z 坐标的考虑得到的。

有关二维图形几何变换的讨论，基本上都适合三维空间。从应用角度来看，三维空间几何变化直接与显示和造型有关，因此更为重要。

同二维变换一样，三维基本变换都是相对于坐标原点和坐标轴进行的几何变换：有平移、比例、旋转、对称和错切等。

与二维变换类似，引入齐次坐标表示，即：三维空间中某点的变换可以表示成 点的齐次坐标与四阶的三维变换矩阵相乘。

平移变换

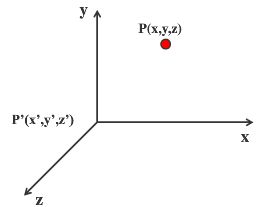
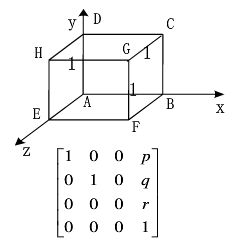
若三维物体沿 x, y, z 方向上移动一个位置，而物体的大小与形状均不变，则称为平移变换。

点 P 的平移变换矩阵表示如下：

比例变换

比例变换分为局部比例变换和整体比例变换。

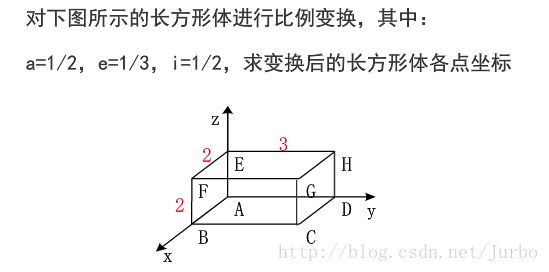
局部比例变换

例子：

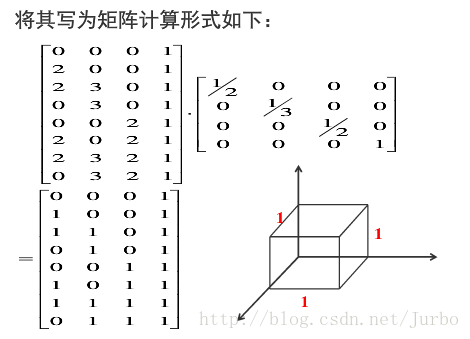
解答：

整体比例变换

旋转变化

三维立体的旋转变化是指给定的三维立体绕三维空间某个指定的坐标轴旋转 θ 角度。旋转后，立体的空间位置将发生变化，但形状不变。

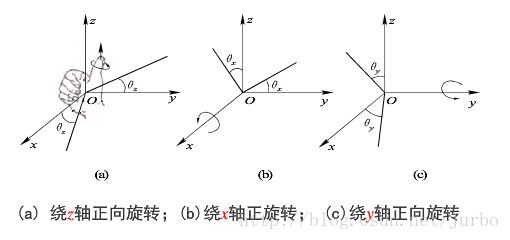
θ 角的正负按右手规则确定，右手大拇指指向旋转轴的正向，其余四个手指指向旋转角的正向。

绕 z 轴旋转 θ

三维空间立体绕 z 轴正向旋转时，立体上各顶点的 x, y 坐标改变，而 z 坐标不变。而 x ,y 坐标可以由二维点绕原点旋转公式得到，由此可得：

绕 x 轴旋转 θ

同理，三维点 p 绕 x 轴正向旋转 θ 角的矩阵计算形式为：

绕 y 轴旋转 θ

三维点 p 绕 y 轴正向旋转 θ 角的矩阵计算形式为：

绕任意轴旋转

求绕任意直线旋转矩阵的原则：

1. 任意变换的问题->基本几何变换的问题
2. 绕任意直线旋转的问题->绕坐标轴旋转的问题

对称变换

对称变换有关于坐标平面、坐标轴等的对称变换。

关于坐标平面的对称变换

关于 xoy 平面进行对称变换的矩阵计算形式为：

关于 yoz 平面进行对称变化的矩阵计算形式为：

关于 zox 平面进行对称变化的矩阵计算形式为：

关于坐标对称的对称变换

关于 X 轴进行对称变换的矩阵计算形式为：

关于 Y 轴进行对称变换的矩阵计算形式为：

关于 Z 轴进行对称变换的矩阵计算形式为：

6.2 投影变换分类

如何在二维平面上显示三维物体？显示器屏幕、绘图纸等都是二维的，显示对象是三维的。

解决方法：投影变换

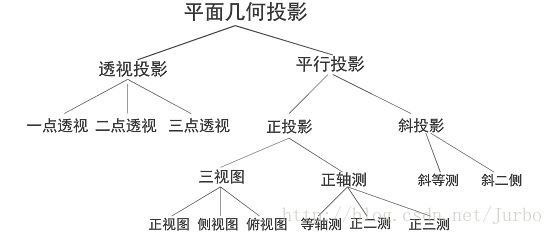
平面几何投影

投影变换就是把三维物体投射到投影面上得到二维平面图形。

需要记住的一点就是，计算机绘图是产生三维物体的二维图像。但在屏幕上绘制图形的时候，必须在三维坐标系下考虑画法。

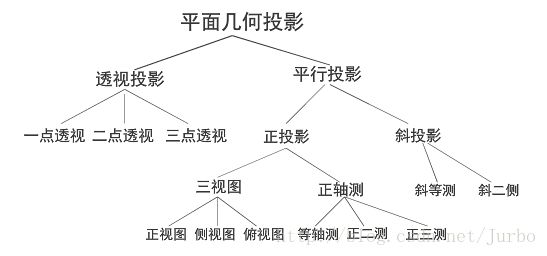
常见的投影法

两种投影法的本质区别在于透视投影的投影中心到投影面之间的距离是有限的，而另一个的距离是无限的。

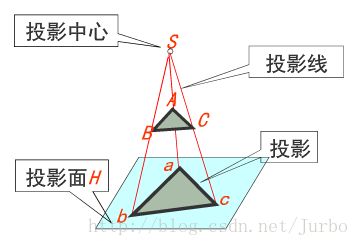
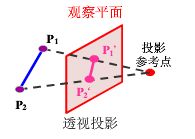
透视（中心）投影

投影线均通过投影中心。在投影中心相对投影面确定的情况下，空间的一个点在投影面上只存在唯一一个投影。

透视投影特点：

• 物体的投影视图由计算投影线与观察平面之交点而得
• 透视投影生成真实感视图但不保持相关比例

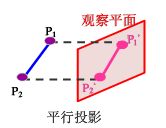
平行投影

如果把透视投影的中心移至无穷远处，则各投影线称为相互平行的直线，这种投影法称为平行投影法。

平行投影特点：

• 平行投影保持物体的有关比例不变
• 物体的各个面的精确视图由平行投影而得
• 没有给出三维物体外表的真实性表示

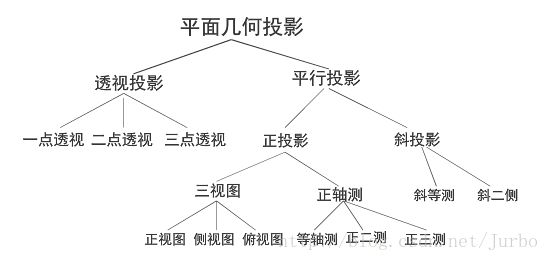
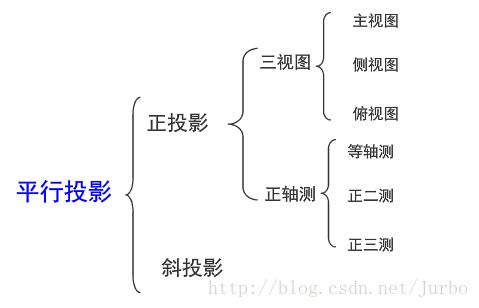
平面几何投影的分类

6.3 平行投影（三视图、轴视图）

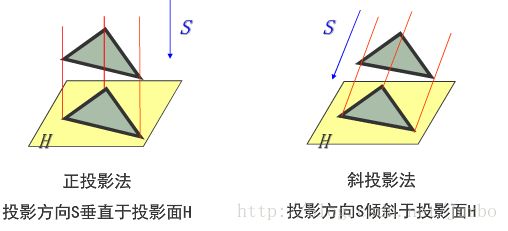
平行投影可根据投影方向与投影面的夹角分成两类：正投影和斜投影。

正投影

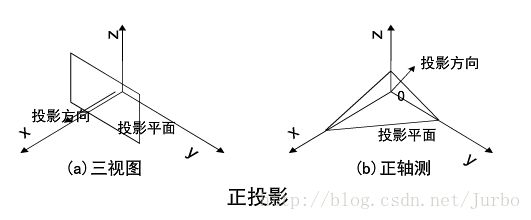
正投影根据投影面与坐标轴的夹角又可分为两类：三视图和正轴侧图。

当投影面与某一坐标轴垂直时，得到的投影为三视图，这是投影方向与这个坐标轴的方向一致。否则，得到的投影为正轴侧图。

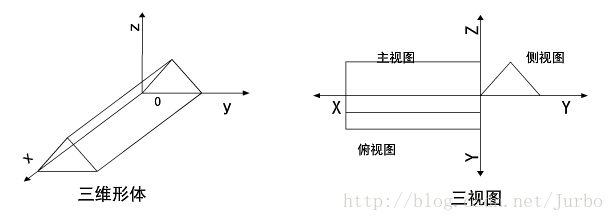
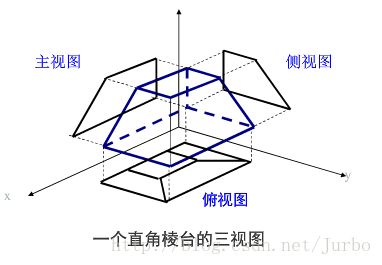
三视图

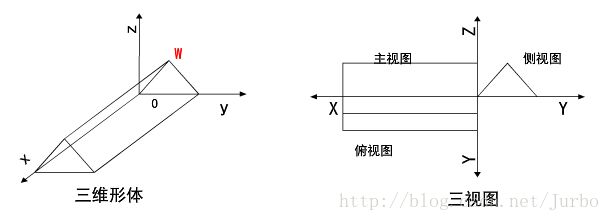
通常所说的三视图包括主视图、侧视图和俯视图三种，投影面分别与 X 轴、 Y 轴、Z轴垂直。

例子

三视图的特点

物体的一个坐标面平行于投影面，其投影能反应形体的实际尺寸。工程制图中常用三视图来测量形体间的距离、角度以及相互位置关系

三视图缺点

三视图只有物体一个面的投影，所以三视图难以形象地表示出形体的三维性质，只有将主视图、侧视图、俯视图三个视图放在一起，才能综合处物体的空间形状。

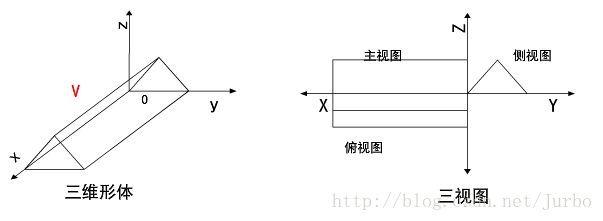
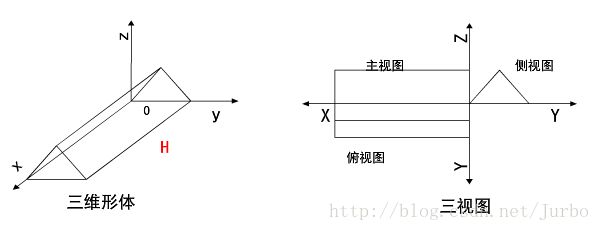
三视图的计算

主视图、俯视图和侧视图是分别将三维物体对正面、水平面和侧面作正平行投影而得到的三个基本视图。

显然，只要 求得这种正平行投影的变换矩阵，就可以得到三维物体上任意点经变换后相应点，有这些变换后的点即可绘出三维物体投影后的三视图。

具体计算步骤如下：

1. 确定三维物体上各点的位置坐标
2. 引入齐次坐标，求出所作交换相应的交换矩形
3. 将所变换用矩阵表示，通过运算求得三维物体上各点经变换后的点坐标值
4. 由变换后得到的二维点绘出三维物体投影后的三视图

主视图

将三维物体 x0z 面（又称 V 面）作垂直投影，得到主视图。

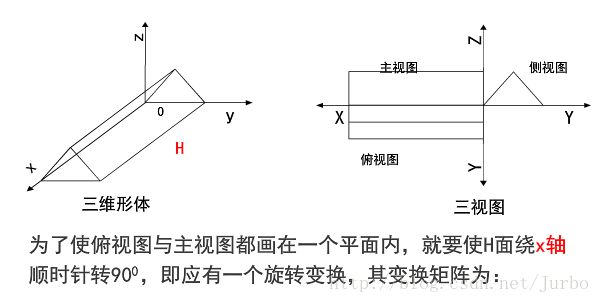
俯视图

将三维物体 x0y 面做垂直投影得到的俯视图。

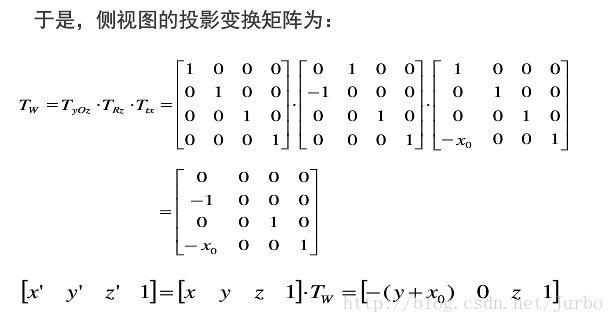
侧视图

将三维物体 y0z面 作垂直投影得到侧视图。

正轴测图投影变换矩阵

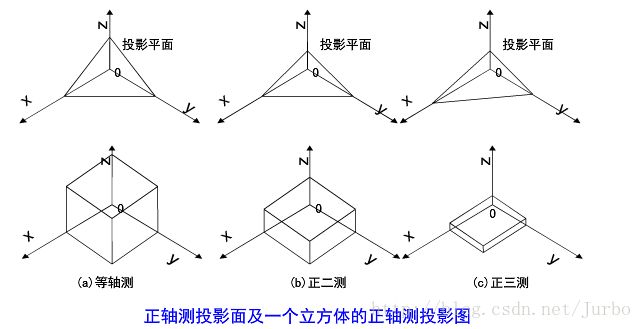
正轴测有等轴侧、正二测和正三测三种：

• 当投影面与三个坐标轴之间的夹角都相等时为等轴侧
• 当投影面与两个坐标轴之间的夹角相等时为正二测
• 当投影面与三个坐标轴之间的夹角都不相等时为正三测

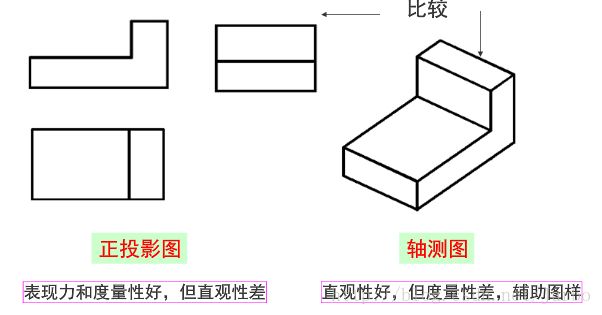
正投影图和轴测图

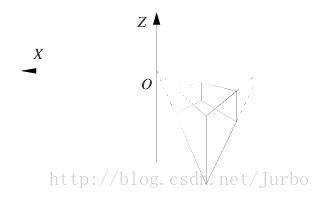
空间中的正轴测图：

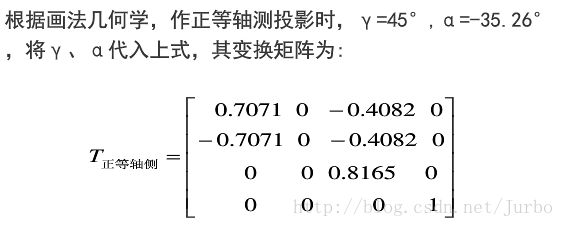
正等轴测图的变换矩阵

正二测图的变换矩形

6.4 透视投影

透视投影表示真实看到的物体。

透视投影是为了获得接近真实三维物体的视觉效果而在二维的纸或者画布平面上绘图或者渲染的一种方法，能逼真地反映形体的空间形象，也称为透视图。

透视投影是3D渲染的基本概念，也是3D程序设计的基础。

轴侧投影图是用平行投影法形成的，视点在无穷远处；而透视投影图是用中心投影法形成的，视点在有限远处。

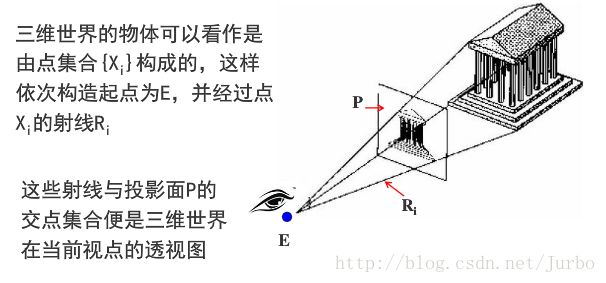
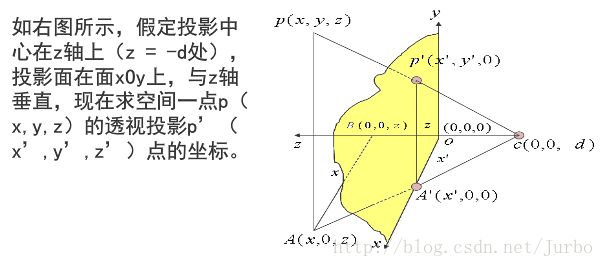
透视基本原理

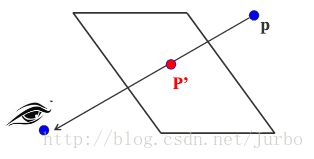
众所周知，位于空间的任何一个点，它之所以能被人们的眼睛所可见，是因为从改点处发射出来的一条光线能够到达人们的眼睛。

该平面为透视投影面，穿点 P’ 为P的透视投影。假如是求空间点的透视投影问题得到了解决，那么空间任何线段、多边形或立体的透视投影也就可以方便地求得。

因为一条直线段是由两点确定，多边形平面由围成该多边形的各个顶点和边框线段确定，而任何立体也可以看成是由它的顶点和各邻边所构成的一个矿体。

这就是说，可以通过求出这些顶点的透视投影而获得空间任意立体的透视投影。

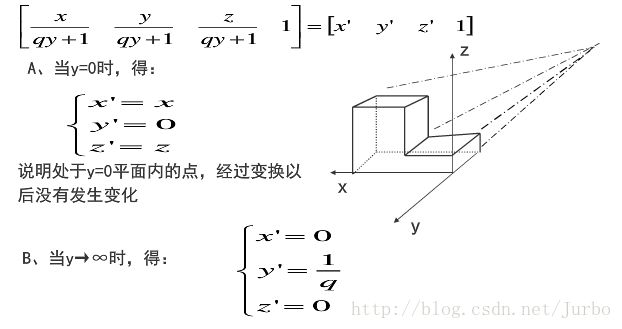
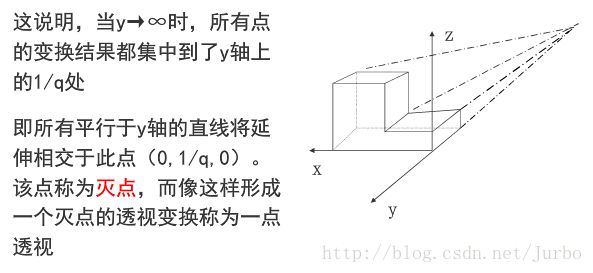
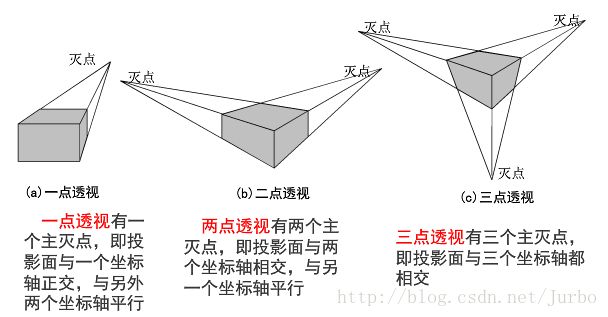
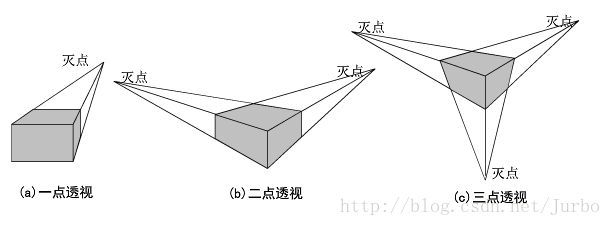
一点透视

多点透视

生成透视投影图的方法

透视投影实例

一点透视

一点透视只有一个灭点。进行透视投影，要很好地考虑图面布局，以避免三维物体的平面或直线积聚成直线或点而影响直观性。具体地说，就是要考虑下列几点：

1. 三维形体与画面（投影面）的相对位置
2. 视距，即视点（投影中心）与画面的距离
3. 视点的高度

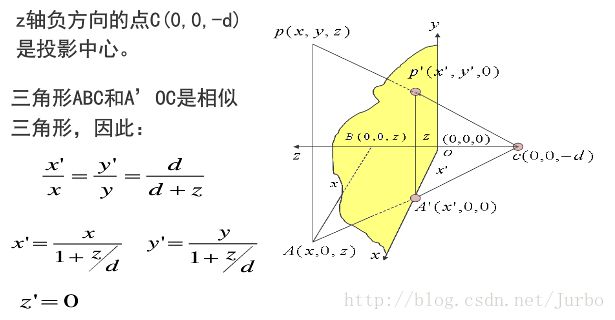
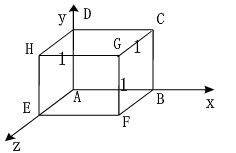
假定视点（投影中心）在 z 轴上（z= -d 处），投影面在 x0y上，则一点透视的步骤如下：

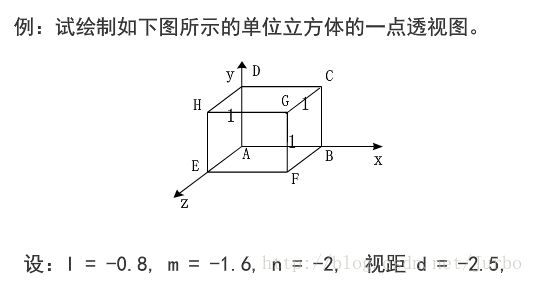
例子：

单位立方体的一点透视

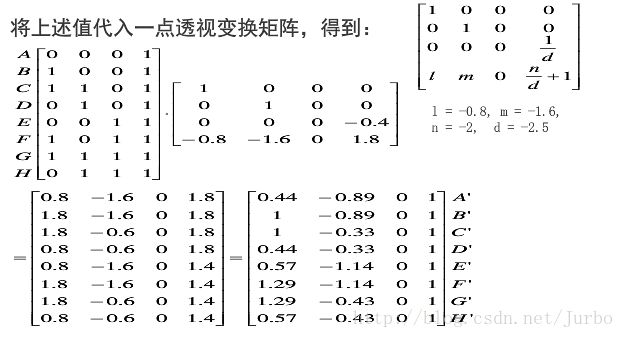
二点透视投影图的生成

做二点透视时，通常要将物体绕 y 轴旋转 θ 角，以使物体的主要平面不平行于投影面。

经透视变换后使物体产生变形，然后再向投影面做正投影。

构造二点透视的一般步骤：

1. 将物体平移到适当位置 l、m、n
2. 将物体绕 y 轴旋转 θ 角
3. 进行透视变换
4. 最后向 xoy 面做正投影，即得二点透视图

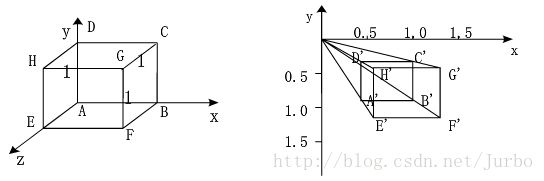
变换结果如下图所示：

三点透视投影图的生成

构造三点透视的一般步骤如下：

1. 将物体平移到适当位置
2. 将物体绕 y 轴旋转 θ 角
3. 再绕 x 轴旋转 α 角
4. 进行透视变换
5. 最后向 xoy 面做正投影，即得三点透视图

6.5 三维图形变化小结

三维物体基本几何变换

三维物体的几何变换是在二维方法基础上增加对 z 坐标的考虑而得到的，有关二维图形几何变换的讨论，基本上都适合于三维空间。

三维物体的投影变换

两种投影法的本质区别在于：透视投影的投影中心到投影面之间的距离是有限的，而另一个的距离是无限的。

平行投影的特点

• 平行投影保持物体的有关比例不变
• 物体的各个面的精确视图由平行投影而得
• 没有给出三维物体外表的真实性表示

透视投影的特点

• 物体的投影视图由计算投影线与观察平面之交点而得
• 透视投影生成真实感视图但不保持相关比例
• 透视投影比轴测图更富有立体感和真实感