遗传算法求解TSP问题（C++实现）

【问题定义】

1. 巡回旅行商问题

给定一组n个城市和俩俩之间的直达距离，寻找一条闭合的旅程，使得每个城市刚好经过一次且总的旅行距离最短。
TSP问题也称为货郎担问题，是一个古老的问题。最早可以追溯到1759年Euler提出的骑士旅行的问题。1948年，由美国兰德公司推动，TSP成为近代组合优化领域的典型难题。
TSP是一个具有广泛的应用背景和重要理论价值的组合优化问题。 近年来，有很多解决该问题的较为有效的算法不断被推出，例如Hopfield神经网络方法，模拟退火方法以及遗传算法方法等。

2. 遗传算法

基本遗传算法可定义为一个8元组：
$（SGA）=（C，E，P0，M，\Phi ，Г，\Psi ，T）$
$C$ ——个体的编码方法，SGA使用固定长度二进制符号串编码方法；
$E$ ——个体的适应度评价函数；
$P0$——初始群体；
$M$ ——群体大小，一般取$20—100$；
$Ф$——选择算子，$SGA$使用比例算子；
$Г$——交叉算子，$SGA$使用单点交叉算子；
$\Psi$——变异算子，$SGA$使用基本位变异算子；
$Т$——算法终止条件，一般终止进化代数为$100—500$；

3. 问题的表示

对于一个实际的待优化问题，首先需要将其表示为适合于遗传算法操作的形式。用遗传算法解决TSP，一个旅程很自然的表示为n个城市的排列，但基于二进制编码的交叉和变异操作不能适用。
路径表示是表示旅程对应的基因编码的最自然，最简单的表示方法。它在编码，解码，存储过程中相对容易理解和实现。例如：旅程（5-1-7-8-9-4-6-2-3）可以直接表示为（5 1 7 8 9 4 6 2 3）
（1）产生初始种群
一是完全随机产生，它适合于对问题的解无任何先验知识的情况。随机性较强，因而也较公正
二是某些先验知识可转变为必须满足的一组要求，然后在满足这些要求的解中在随机地选取样本。这样选择初始种群可使遗传算法更快的达到最优解。种群有一定的目标性和代表性，但取例不如完全随机的广泛，而且先验知识是否可靠也是一个问题
（2）适应度函数
遗传算法在进化搜索中基本不利用外部信息,仅以适应度函数为依据,利用种群中每个个体的适应度值来进行搜索。TSP的目标是路径总长度为最短，路径总长度的倒数就可以为TSP的适应度函数：
选择
一般地说，选择将使适应度较大(优良)个体有较大的存在机会，而适应度较小（低劣）的个体继续存在的机会也较小。简单遗传算法采用赌轮选择机制，令Σfi表示群体的适应度值之总和，fi表示种群中第i个染色体的适应度值，它产生后代的能力正好为其适应度值所占份额fi／Σfi。
（3）交叉
基于路径表示的编码方法，要求一个个体的染色体编码中不允许有重复的基因码，也就是说要满足任意一个城市必须而且只能访问一次的约束。基本遗传算法的交叉操作生成的个体一般不能满足这一约束条件。
部分匹配交叉操作要求随机选取两个交叉点，以便确定一个匹配段，根据两个父个体中两个交叉点之间的中间段给出的映射关系生成两个子个体
例如，对下面两个父个体的表示，随机地选择两个交叉点“/”
$P1：(123/4567/89)，P2：（452/1876/93）$
首先，两个交叉点之间的中间段交换，得到：
$o1：(xxx/1876/xx)，o2：(xxx/4567/xx)$
其中x表示暂时未定义码，得到中间段的映射关系。，有：
1----4，8----5，7----6，6----7
对子个体1，2中的x部分，分别保留从其父个体中继承未选定城市码，得到： $o1：(x23/1876/x9)，o2：(xx2/4567/93)$
最后，根据中间段的映射关系，对于上面子个体1的第一个x，使用最初父码1，由1----4
交换得到第一个x为4，类似地子个体1的第二个x，使用最初父码8，由8----5交换得到子个体1的第二个x为5。类似地进行操作，最终得到的子个体为：
$o1：(423/1876/59)，o2：(182/4567/93)$
（4）变异
遗传算法解决TSP 问题基于二进值编码的变异操作不能适用，不能够由简单的变量的翻转来实现
在TSP问题中个体的编码是一批城市的序列，随机的在这个序列抽取两个城市，然后交换他们的位置。这样就实现了个体编码的变异，算法如下：
产生两个0到1之间的随机实数；
将这两个随机实数转化为0到n（城市数）-1之间的随机整数；
将这两个随机整数指代的城市进行交换；

【实验原理】

1. 巡回旅行商问题（$TSP$）
   给定一组$n$个城市和俩俩之间的直达距离，寻找一条闭合的旅程，使得每个城市刚好经过一次且总的旅行距离最短。
2. 遗传算法
   （1）在论域空间上定义一个适应度函数$f(x)$，给定种群规模$N$，交叉率$Pc$和变异率$Pm$，代数$T$；
   （2）随机产生$U$中的$N$个染色体$s1,s2,\dots ,sN$，组成初始种群$S=s1,s2,\dots ,sN$，置代数计数$t=1$；
   （3）计算$S$中每个染色体的适应度$f()$；
   （4） 若终止条件满足，则取$S$中适应度最大的染色体作为所求结果，算法结束；
   （5）按选择概率$p(si)$所决定的选中机会，每次从$S$中随机选中$1$个染色体并将其复制，共做$N$次，然后将复制得到的$N$染色体组成群体$S1$；
   （6）按$Pc$所决定的参加交叉的染色体数$c$，从$S1$中随机确定$c$个染色体，配对进行交叉操作，并用产生的染色体代替原染色体，组成群体$S2$；
   （7）按$Pm$所决定的变异次数$m$，从$S2$中随机确定$m$个染色体，分别进行变异操作，并用产生的新染色体代替原染色体，组成群体$S3$；
   （8）将群体$S3$作为新种群，即用$S3$代替$S$，$t=t+1$，转（3）。

【实验内容】

用遗传算法求解TSP问题

1. 基本要求

（1）$N>=8$。
（2）随即生成$N$个城市间的连接矩阵。
（3）指定起始城市。
（4） 给出每一代的最优路线和总路线长度。
（5）以代数$T$作为结束条件，$T>=50$。

2. 程序代码

#include
#include
#include
#include
#include
#include
#define ERROR -1
using namespace std;

typedef struct City
{
	int x,y;	// 城市坐标
}City;
City cities[10];
double distance(int a, int b)	// 计算两城市间距离
{
	return abs((cities[a].x - cities[b].x) ^ 2 + (cities[a].y - cities[b].y) ^ 2);
}

int gene_sum = 9;	// 染色体上的基因数
class Population;	// 向前引用，种群类
class Chro	// Chromoesome染色体
{
public:
	Chro();	// 构造函数，将适应度初始化为0
	void RandomInit();	// 随机初始化
	double fx();		// 适应度函数
	void display();		// 展示基因序列
	void copy(Chro s);	// 复制
	void exchange(Chro &s);// 互换
	void variation();	// 变异
	friend int find(int gene[], int start, int end, int x);	// 寻找基因x在染色体上的位置
	friend class Population;
private:
	int *gene;
	double fits;	// 适应度
};
Chro::Chro()
{
	gene = new int[gene_sum];
	fits = 0;
}
void Chro::RandomInit()	// 随机初始化染色体上的基因序列
{
	int i;
	time_t t;
	for (i = 0; i < gene_sum; i++) {
		gene[i] = i;
	}
	srand((int)time(&t));// 确保不会生成重复的随机数
	for (i = 0; i < 1+int(gene_sum/2); i++) {
		swap(gene[i], gene[i + rand() % (gene_sum - i)]);
	}
	fx();
	Sleep(1000);
}
double Chro::fx()	//	适应度函数fx
{
	double f = 0;
	for (int i = 0; i < gene_sum; i++){
		f += distance(gene[i], gene[(i + 1) % gene_sum]);
	}
	fits = 1.0 / f;// 总距离越大，适应度越小
	return fits;
} 
void Chro::display()	// 展示基因序列和该染色体适应度
{
	cout << "    [";
	for (int i = 0; i < gene_sum; i++) {
		cout << " " << gene[i];
	}
	cout << " ],  fits= " << fx()<<", distance= "<<1/fx();
}
void Chro::copy(Chro s)	//复制
{
	for (int i = 0; i < gene_sum; i++){
		gene[i] = s.gene[i];
	}
	fits = fx();	// 重新计算适应度
}
int find(int gene[], int start, int end, int x)// 在gene序列中查找x基因的位置并返回
{
	for (int i = start; i <= end; i++) {
		if (gene[i] == x) {
			return i;
		}
	}
	return ERROR;
}
void Chro::exchange(Chro &s)	//将当前染色体与另一染色体s进行基因片段交换
{
	int i, j = 0, k = 0, repeat;
	int pos = rand() % (gene_sum - 4);	// 随机选择交叉位置（由于要交换3或4个基因，所以交叉位置只能在[1，n-4]内）
	int num = 3 + rand() % 2;	// 随机选择交叉的基因数，最小为3，最大为4
	/*
	cout << endl; 查看发生交换的位置和位数
	cout << "pos: " << pos << ", num: " << num << endl;*/

	int *segment1 = new int[gene_sum];	// 用于记录交换后当前染色体上的基因
	int *segment2 = new int[gene_sum];	// 用于记录交换后另一染色体上的基因
	for (i = 0; i < gene_sum; i++) {
		if (i >= pos && i < pos + num) {
			segment1[i] = s.gene[i];
			segment2[i] = gene[i];
		}
		else {
			segment1[i] = gene[i];
			segment2[i] = s.gene[i];
		}
	}

	int *mapping1 = new int[4];	// 当前染色体中间段的映射
	int *mapping2 = new int[4];	// 另一染色体中间段的映射
	for (i = 0; i < 4; i++) {
		mapping1[i] = ERROR;	// 初值全部为-1
		mapping2[i] = ERROR;
	}
	for (i = pos; i < pos + num; i++) {
		repeat = find(segment1, pos, pos + num - 1, gene[i]);
		if (repeat == ERROR) {
			mapping1[j++] = gene[i];	
		}
		repeat = find(segment2, pos, pos + num - 1, s.gene[i]);
		if (repeat == ERROR) {
			mapping2[k++] = s.gene[i];
		}
	}
	/* 查看映射
	cout << "map1   " << "map2" << endl;
	for (k = 0; k < 4; k++) {
		cout << mapping1[k] << "     " << mapping2[k] << endl;
	}*/

	j = k = 0;
	for (i = pos; i < pos + num; i++) {// 将重复的基因替换为映射中的基因
		repeat = find(gene, 0, pos - 1, segment1[i]);
		if (repeat != ERROR) {
			segment1[repeat] = mapping1[j++];
		}
		repeat = find(gene, pos + num, gene_sum - 1, segment1[i]);
		if (repeat != ERROR) {
			segment1[repeat] = mapping1[j++];
		}
		repeat = find(s.gene, 0, pos - 1, segment2[i]);
		if (repeat != ERROR) {
			segment2[repeat] = mapping2[k++];
		}
		repeat = find(s.gene, pos + num, gene_sum - 1, segment2[i]);
		if (repeat != ERROR) {
			segment2[repeat] = mapping2[k++];
		}
	}
	for (i = 0; i < gene_sum; i++) {
		gene[i] = segment1[i];	// 交叉后的该染色体
		s.gene[i] = segment2[i];// 交叉后的另一染色体
	}
	delete segment1;
	delete segment2;
	delete mapping1;
	delete mapping2;
}
void Chro::variation()
{
	int pos = rand() % 8;	// 随机选择变异位置
	int temp = gene[pos];	// 将被选中的基因和后面一位基因交换
	gene[pos] = gene[pos + 1];
	gene[pos + 1] = temp;
}

Chro solution;	// 用于记录有史以来最好的染色体
int best_generation = 0;	// 用于记录最好的染色体所在的代数
int chro_sum = 20;	// 种群中染色体数
class Population
{
public:
	Population();	// 构造函数
	void best_fit();// 查找适应度最高的染色体
	void select();	// 选择
	void cross();	// 交叉
	void variation();// 种群变异
	void display();	// 显示种群内染色体
	int generation; // 种群代数
private:
	Chro *chromoesomes;	// 染色体
	double Σf;	// 种群适应度之和
	double *P;	// 选择概率
};
Population::Population()
{
	int i;
	generation = 1;
	chromoesomes = new Chro[chro_sum];
	for ( i = 0; i < chro_sum; i++){
		chromoesomes[i].RandomInit();
	}
	Σf = 0;
	P = new double[chro_sum];
	for (i = 0; i < chro_sum; i++) {
		Σf += chromoesomes[i].fits;
	}
	for (i = 0; i < chro_sum; i++) {
		P[i] = chromoesomes[i].fits / Σf;
	}
}
void Population::best_fit()	// 查找适应度最大的染色体并返回其编号
{
	int best = 0;
	for (int i = 1; i < chro_sum; i++){
		if (chromoesomes[best].fx() < chromoesomes[i].fx()) {
			best = i;
		}
	}
	if (chromoesomes[best].fx() > solution.fits) {
		solution.copy(chromoesomes[best]);
		best_generation = generation;
	}
	cout << "  The best fit in generation" << generation << " is: " << endl;
	cout << "  chromoesomes" << best + 1 << ": ";
	chromoesomes[best].display();
	cout << endl;
}
void Population::select()	// 种群选择
{
	int i, j;
	int *selected = new int[chro_sum];	// 用于记录被选中的染色体号
	double r;
	double *q = new double[chro_sum];	// 用于记录积累概率
	Chro *cp = new Chro[chro_sum];
	q[0] = P[0];	// 积累概率
	cout << endl;
	cout << "  Accumulation of probabilities" << endl;	// 打印积累概率
	cout << "  q1= " << q[0] << endl;
	for (i = 1; i < chro_sum; i++) {
		q[i] = q[i - 1] + P[i];
		cout << "  q" << i + 1 << "= " << q[i] << endl;
	}
	cout << "\n  Roulette wheel" << endl;// 轮盘赌，产生随机数
	srand(time(NULL));//设置随机数种子，使每次产生的随机序列不同
	for (int i = 0; i < chro_sum; i++){
		r = rand() % (10000) / (double)(10000);
		cout << "  r" << i + 1 << "= " << r << endl;
		if (r <= q[0]) {
			selected[i] = 0;	// 选中第一个染色体
		}
		for (j = 0; j < chro_sum - 1; j++){
			if (q[j] <= r && r <= q[j + 1]) {
				selected[i] = j + 1;	// 选中第j+1个基因
			}
		}
		cp[i].copy(chromoesomes[i]);
	}
	for (i = 0; i < chro_sum; i++){
		chromoesomes[i].copy(cp[selected[i]]);
	}
	delete selected;
	delete q;
	delete cp;
}
void Population::cross()	// 种群交叉
{
	for (int i = 0; i < chro_sum; i += 2) {
		chromoesomes[i].exchange(chromoesomes[i + 1]);
	}
}
void Population::variation()	// 种群变异
{
	int probability = rand() % 100;	// 变异积累为1%
	if (probability==1){
		int x = rand() % chro_sum;	// 随机选择一个染色体变异
		cout << "  The chromoesome " << x << " is variated!" << endl;
		chromoesomes[x].variation();
	}
	generation++;	// 至此，种群进化一代
}
void Population::display()// 依次输出每一条染色体（每种方案）
{
	cout << endl;
	int i;
	for (i = 0; i < chro_sum; i++) {	
		cout << "  chromoesomes" << i + 1 << ": ";
		chromoesomes[i].display();
		cout << endl;
	}
	cout << endl;
}

int main()
{
	cout << "  Input the number of cities:  ";	// 输入城市数(基因数)
	cin >> gene_sum;
	cout << "  Input the number of chromoesomes in population:  ";// 输入染色体数
	cin >> chro_sum;
	cout << "  Input the location of cities:" << endl;// 输入每个城市坐标(x, y)
	for (int i = 0; i < gene_sum; i++){
		cout <<"\t"<< i + 1 << ": ";
		cin >> cities[i].x >> cities[i].y;
	}
	Population P0;
	cout << "\n  Generation=" << P0.generation << endl;
	P0.display();
	P0.best_fit();
	int T;	// 进化的代数
	cout << "  Input the T:  ";
	cin >> T;
	for (int i = 0; i < T; i++) {
		cout << endl << "  After select: ";	// 选择
		P0.select();
		P0.display();
		cout << endl << "  After cross: ";	// 交叉
		P0.cross();
		P0.display();
		cout << endl << "  After variation: ";// 变异
		P0.variation();
		cout << "  Generation=" << P0.generation << endl;
		P0.display();
		P0.best_fit();
		system("pause");
		system("cls");
	}
	cout << "  The best solution in history is:" << endl;	// 打印进化过程中最好的染色体，即解决方案
	cout << "  in generation" << best_generation;	
	solution.display();
	cout << endl;
	system("pause");
	return 0;
}

3. 程序运行说明

（1）手动输入城市个数，这里设为$9$；手动输入染色体数，这里设为$20$，手动输入$9$个城市坐标，随后生成$20$条不同的染色体。

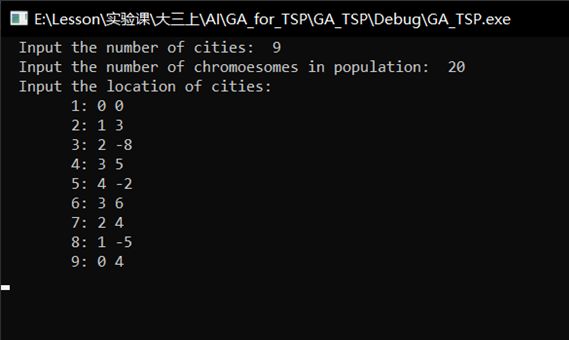
初始种群中，适应度最高的染色体是第$14$条。输入进化的代数T为$100$代

（2）第一代种群进行选择，这里先输出积累概率和轮盘赌的结果，再显示选择后的种群。

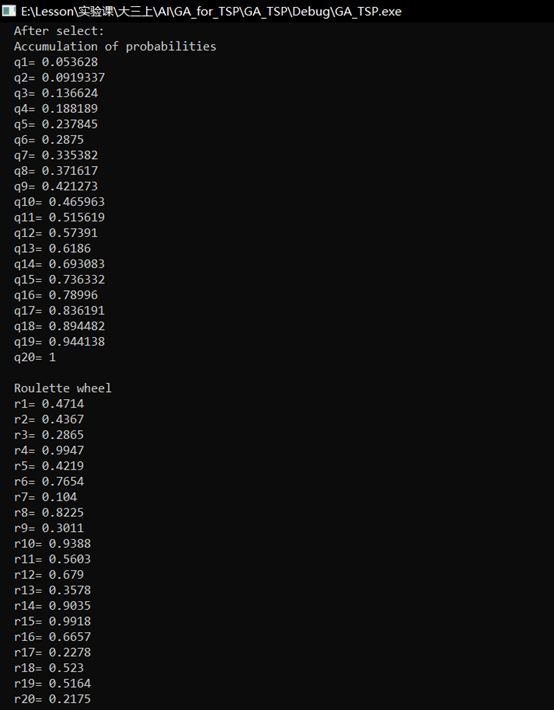
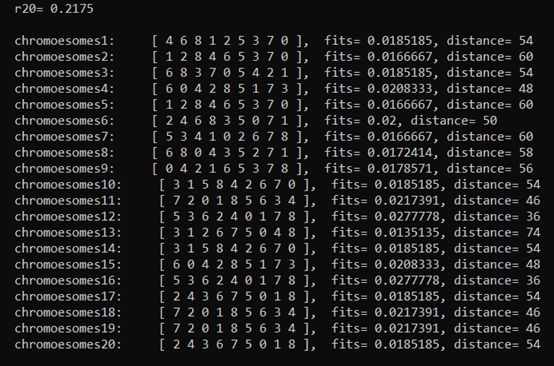
（3）种群选择过后，进行染色体交叉（代码中有关于打印映射函数的部分，这里不做观察，将其注释）

（4）种群交叉后，再进行变异（这一轮没有染色体发生变异）。至此，种群已经进化一代。

（5）按下回车，屏幕刷新，第二代种群开始进行选择、交叉、变异，生成第三代种群（这次依然没有发生变异）


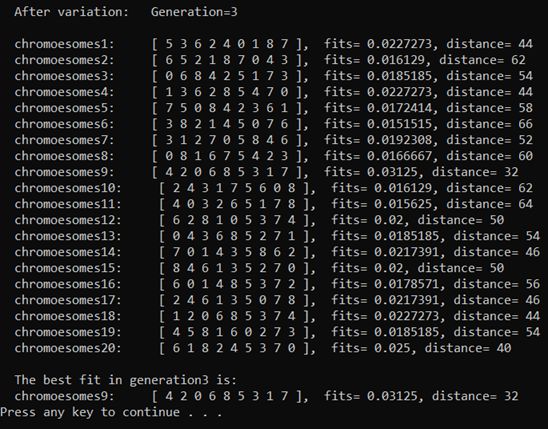
（6）这里设定的变异率为$1$%，在第$95$代种群进化到第$96$代的过程中发生了变异。

（7）进化完$100$代，算法结束

（8）显示种群进化过程中适应度最高的染色体
据此得知最佳解决方案在第$9$代种群中，适应度为$0.033333$，路径为$1-4-2-7-0-5-3-8-6$，距离为$30$。

【小结或讨论】

通过本次实验，我完成了遗传算法求解旅行商问题，进一步理解了遗传算法的基本流程。实验数据中的适应度较低是由于适应度为距离的倒数，城市坐标位置将一定程度上影响总体适应度的值，但不会影响进化结果。通过时间生成初始种群中染色体上的基因序列，为避免生成相同的染色体，使用了sleep()函数来调节伪随机数，运行到输入完城市坐标的部分后会停止种群中染色体数*1000ms的时间。交叉函数中，从1到（染色体基因数-4）的位置任意选取一个作为交叉开始位置，连续的3或4位发生交换。设置了映射函数避免交叉后基因重复。实验中输入的城市数量为9较小，染色体数量20和进化代数100较大，导致在进化过程中的适应度趋于固定的几个数。