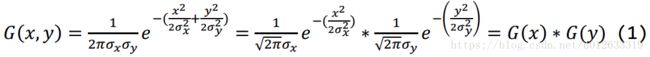高斯滤波（C++实现）

一维高斯函数：
$$G(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{x^2}{2{\sigma }^2}}$$
二维高斯函数：
$$G(x,y)=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{x^2+y^2}{2{\sigma }^2}}$$

下面我们计算高斯核用的函数是：
$$G(x,y)=e^{-\frac{x^2+y^2}{2{\sigma }^2}}$$

double** myGetGaussianKernel(int size, double sigma)
{
	double sum = 0.0;
	int center = size/2; // 用于计算中心点的坐标

	double** arr = new double*[size];
	for(int i=0; i

二维高斯函数可以看成两个一维高斯函数的乘积。

// C++高斯滤波
void myGaussianBlur(const Mat _src, Mat& _dst, int size, double sigma)
{
	if(!_src.data) return;
	Mat src = _src.clone();
	Mat dst(src.size(), src.type(), Scalar::all(0));
	double** gaus = myGetGaussianKernel(size, sigma);
	// 等价于
	// Mat_ gaus = getGaussianKernel(3,1,CV_64F);
	// gaus = _gaus * _gaus.t();
	
	int center = size/2;

	copyMakeBorder(_src, src, center, center, center, center, BORDER_REPLICATE);

	for(int i=center; i(i-center, j-center)[0] += src.at(i+x, j+y)[0] * gaus[x+center][y+center];
					dst.at(i-center, j-center)[1] += src.at(i+x, j+y)[1] * gaus[x+center][center];
					dst.at(i-center,j-center)[2] += src.at(i+x, j+y)[2] * gaus[x+center][center];
				}
			}
		}
	}
	dst.copyTo(_dst);
}

参考资料：
[1] openCV之高斯滤波（及代码实现）
[2] OpenCV 源码分析-getGaussianKernel
[3] 基于C++&OpenCV实现高斯滤波【数字图像处理】
[4] 高斯滤波的C++实现与优化