遗传+粒子群 求解多配送中心车辆调度问题（python）

双层规划模型的车辆路径优化问题（python3）

考虑将粒子群算法与遗传算法结合起来研究车辆路径优化问题。

1.问题描述

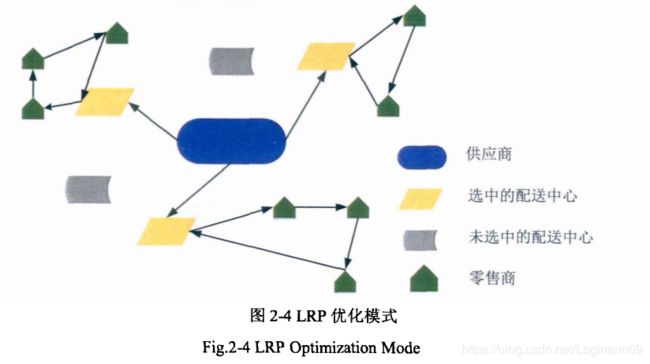
LRP 问题既可以满足配送中心的最优数量和容量，又可以确定车辆的最优运输路线 ，是LAP问题（物流配送中心选址问题）和VRP问题的集成 。它可以描述为：至少有一 个位置及容量均己知的配送中心，若干个位置及需求量均己知的终端零售商，承载量己知的车辆若干，在这些约束条件下 ，选择出最佳配送中心选址方案和最优配送路径优化方案，从而使物流成本最低 、物流效率最高 。

建立双层规划模型求解该问题。上层规划是从好几个配送中心中选择出一个或多个配送中心的问题，下层规划是车辆配送方案的确定问题（也就是带时间窗的VRP问题），主要目的是通过上下层规划模型的相互作用达到冷链物流配送开放式车辆路径优化的目的。

2.算法实现过程介绍

当我兴致勃勃以为很简单的时候，才发现这多个配送中心并没有指定具体的客户，也就是说存在至少以下三个决策变量：（1）确定到底选择哪个配送中心以及选择配送中心的个数是一个还是多个；（2）确定配送中心到底服务哪些客户，以便决定车辆从配送中心到客户点间的距离矩阵；（3）车辆服务客户的顺序。

查阅文献，发现针对多配送中心的车辆调度问题，其中确定配送中心服务哪些客户的这个决策因素，采取的相对简单的方法是：最近分配方法。该方法的具体操作是通过计算某客户与各配送中心的距离，该客户离哪个配送中心最近，就将其分配给哪个配送中心 。

多配送中心车辆调度问题的算法步骤如下：
（1）先通过就近分配原则，确定配送中心的服务客户，降低问题的复杂度，将多配送中心问题转化为单配送中心问题求解；
（2）采用双层规划模型求解多配送中心的车辆调度问题。
上层模型求解到底需要几个配送中心的问题，采用遗传算法；下层模型在确定好配送中心的前提下解决VRPTW问题，采用粒子群算法。

3.关键技术

3.1 将粒子群算法封装成类

遗传算法和粒子群算法的常用函数，我在前两篇博文中已经给出了，就是将两种算法整合在一起进行调整的过程。下层模型如果重新定义粒子的编码结构，会增加求解的难度，既然多配送中心的问题转换成了一般的单配送中心问题，将文章提到的粒子群算法封装成类，多次调用就可以得到各个被选中的配送中心的总运输成本。

3.2 利用备忘录法记录遗传算法已经求解过的染色体

当备选配送中心的数量很小时，完全可以利用枚举的方式列出全部的可行解集合，例如，考虑三个配送中心，应该选择哪几个作为实际建设的配送中心以优化物流运输成本，将可行解的集合看作是S，S=｛｛1｝，｛2｝，｛3｝，｛1,2｝，｛1,3｝，｛2,3｝，｛1,2,3｝｝，一共有7种选择方案。可以利用python的itertools模块列出集合的全部子集（不包括空集），代码如下：

from itertools import combinations
L = [1, 2, 3]
result_list = sum([list(map(list, combinations(L, i))) for i in range(1, len(L) + 1)], [])
print('result_list =', result_list)

当备选配送中心的数量较大时，全部的非空子集个数为：2的n次方减1。可以通过遗传算法的进化规则使一些较劣解不参与计算，从而降低问题求解的规模。

4.算例代码

上层选择配送中心建设方案的过程采用枚举算法。

#!/usr/bin/python3
# -*- coding: utf-8 -*-
# @Author : Logintern09


from VRPTW_data import Data_class
import numpy as np
np.set_printoptions(threshold=np.inf)  # 保证数组全部显示出来
from PSO_func import *


demand_distance_graph = Data_class.demand_distance_graph  # 需求点的距离矩阵
supply_distance_graph = Data_class.supply_distance_graph  # 供给点的距离矩阵
demand_node_num = Data_class.demand_node_num  # 需求节点的数量
supply_node_num = Data_class.supply_node_num  # 供给节点的数量

data_dict = dict()
data_dict['demand_quantity'] = Data_class.demand_quantity
data_dict['demand_time_window'] = Data_class.demand_time_window
data_dict['demand_service_time'] = Data_class.demand_service_time
data_dict['mile_max'] = 1000  # 每辆车的最大行驶里程数
data_dict['vehicle_capacity_max'] = 15  # 车辆的最大载重量
data_dict['unit_trans_cost'] = 10  # 配送中心到需求点，车辆的单位运输成本，单位：元/公里
data_dict['vehicle_useCost'] = 300  # 车辆的使用成本，单位：元
data_dict['vehicle_speed'] = 40  # 配送中心到需求点，车辆的单位行驶速度，单位：公里/小时
data_dict['vehicle_num'] = 4  # 供配送中心调配的车辆数
data_dict['unit_ET_cost'] = 0.5  # 早到机会惩罚成本系数
data_dict['unit_LT_cost'] = 1.5  # 不满足时间窗要求的晚到单位惩罚成本
data_dict['unit_loss_cost'] = 0.5  # 单位货损成本系数
data_dict['unit_built_cost'] = 0  # 配送中心的单位建设成本


# 确定粒子群算法的参数
pso_parameter_dict = dict()
pso_parameter_dict['population_size'] = 100  # 粒子种群的大小
pso_parameter_dict['max_steps'] = 200
pso_parameter_dict['w'] = 0.6  # 惯性权重
pso_parameter_dict['p_c1'] = 2  # 个体学习因子
pso_parameter_dict['g_c2'] = 2  # 社会学习因子
pso_parameter_dict['solution_layer'] = 2  # 问题的自变量有两个，分别是确定车辆与客户的一对一关系，和确定车辆的配送顺序


# 采用最近路径法分配客户给配送中心
def allocation_customer(location_index):
    """
    :param location_index: 选择的配送中心的序号，从小到大排列
    :return:
    location_customer_list: 第i个数组表示location_index-1的顾客集合
    """
    if len(location_index) == 1:
        location_customer_list = []
        location_customer_list.append(range(Data_class.demand_node_num))
        return location_customer_list
    supply_distance_graph = Data_class.supply_distance_graph
    distance = supply_distance_graph[location_index, :]
    customer_to_location = np.argmin(distance, axis=0)
    location = list(set(customer_to_location))
    location.sort()
    location_customer_list = []
    for location_index in location:
        location_customer_list.append(np.where(customer_to_location == location_index)[0])
    return location_customer_list


def get_pathLen_time(supply_index):
    # 正式运算时用到的是distance_graph
    demand_node_num = Data_class.demand_node_num  # 需求节点的数量
    distance_graph = np.zeros((demand_node_num + 1, demand_node_num + 1))
    distance_graph[0, 1:] = supply_distance_graph[supply_index, :]
    distance_graph[1:, 1:] = demand_distance_graph
    distance_graph[1:, 0] = np.transpose(supply_distance_graph[supply_index, :])
    vehicle_speed = Data_class.vehicle_speed
    pathTime_graph = (distance_graph / vehicle_speed) * 60  # 需求点间路段上的行驶时间，单位：分钟
    return distance_graph, pathTime_graph


def cal_built_cost(location_index):
	# 计算配送中心的建设成本
    return len(location_index)*data_dict['unit_built_cost']


# 枚举出所有的可行解，即上层配送中心的选择方案
from itertools import combinations
location_list = range(0, supply_node_num)
upper_list = sum([list(map(list, combinations(location_list, i))) for i in range(1, len(location_list) + 1)], [])

best_routes_list = []
fitness = []
for location_index in upper_list:
    location_customer_list = allocation_customer(location_index)
    ind_routes = []
    ind_value = 0
    for i in range(len(location_index)):
        supply_index = location_index[i]
        demand_nodes = location_customer_list[i]
        demand_nodes = [i+1 for i in demand_nodes]  # 需求节点的编号从1开始
        demand_node_num = len(demand_nodes)
        # 采用粒子群算法针对需求节点的索引进行计算下层模型的成本
        pso_parameter_dict['dim'] = pso_parameter_dict['solution_layer'] * demand_node_num  # 一个粒子的维度
        pso_parameter_dict['x_bound'] = [[1, data_dict['vehicle_num']], [1, demand_node_num]]  # 自变量的上下限限制
        distance_graph, pathTime_graph = get_pathLen_time(supply_index)
        # 初始化粒子群类
        pso = pso_operation(pso_parameter_dict, data_dict,
                            demand_nodes, distance_graph, pathTime_graph,)
        best_routes, best_value = pso.run()
        ind_routes += best_routes
        ind_value += best_value
    # 记录每一个上层可行解的下层解码的结果
    best_routes_list.append(ind_routes)  # ind_routes表示每一条染色体解码得到的路线（包含所有的需求点）
    fitness.append(ind_value + cal_built_cost(location_index))

# 找到成本最小的解
min_value = min(fitness)
index = fitness.index(min_value)
best_solution = best_routes_list[index]
best_supply_solution = upper_list[index]
print('上下层成本最小值：', min_value)
print('下层最优的解结构', best_solution)
print('上层最优的解结构：', best_supply_solution)

# 解码得到各个配送中心的下层车辆配送方案
customer_allocation = allocation_customer(best_supply_solution)
for index in range(len(customer_allocation)):
    allocate_plan = customer_allocation[index]
    allocate_plan = [i+1 for i in allocate_plan]
    routes_plan = []
    for i in range(len(allocate_plan)):
        node = allocate_plan[i]
        for routes in best_solution:
            if node in routes and (routes not in routes_plan):
                routes_plan.append(routes)
    print('%s 配送中心的配送方案为：%s' % (best_supply_solution[index], routes_plan))
    

5.结果展示

备选配送中心的个数为5个。

（1）不考虑配送中心的建设成本，总成本只是下层粒子群算法求解的总运输成本，总运输成本=车辆的固定使用成本+车辆运输路线成本+时间窗的惩罚成本+货损成本。

上下层成本最小值： 6970.5825
下层最优的解结构 [[0, 11, 10, 0], [0, 1, 0], [0, 2, 14, 3, 0], [0, 6, 13, 7, 0], [0, 8, 15, 5, 0], [0, 9, 4, 12, 0]]
上层最优的解结构： [0, 1, 2, 3, 4]
0 配送中心的配送方案为：[[0, 1, 0], [0, 11, 10, 0]]
1 配送中心的配送方案为：[[0, 2, 14, 3, 0]]
2 配送中心的配送方案为：[[0, 6, 13, 7, 0]]
3 配送中心的配送方案为：[[0, 8, 15, 5, 0]]
4 配送中心的配送方案为：[[0, 9, 4, 12, 0]]

（2）考虑上层配送中心的建设成本，当配送中心的建设成本较大时，理论上是少建配送中心，节约固定建设成本。当配送中心的固定建设成本为500时，

上下层成本最小值： 8563.9725
下层最优的解结构 [[0, 3, 14, 1, 0], [0, 11, 10, 0], [0, 13, 2, 6, 0], [0, 8, 7, 0], [0, 5, 15, 4, 12, 9, 0]]
上层最优的解结构： [0, 2, 4]
0 配送中心的配送方案为：[[0, 3, 14, 1, 0], [0, 11, 10, 0]]
2 配送中心的配送方案为：[[0, 13, 2, 6, 0], [0, 8, 7, 0]]
4 配送中心的配送方案为：[[0, 5, 15, 4, 12, 9, 0]]

5.小结

（1）下层的粒子群算法还有待改善。
（2）考虑采用多线程的方式实现下层粒子群算法的同步计算。

参考文献：

1.基于双层规划模型的冷链物流配送开放式车辆路径优化
2.城市生鲜食品冷链物流配送中心选址及路径优化问题研究
3.Python包中__init__.py作用
4.如何基于python生成list的所有的子集