使用sklearn 机器学习基础知识
特征转化数据预处理:
为什么要转化数据呢,就是要让它成为有效的特征,因为原始数据是很多脏数据无用数据的。常用的方法是标准化,归一化,特征的离散化等等
连续型数据处理之二值化:Binarizer
假设淘宝现在有个需求,我得根据年龄来进行物品推荐,把50以上的人分为老年,50以下分为非老年人,那么我们根据二值化可以很简单的把50以上的定为1,50以下的定为0。这样就方便我们后续的推荐了。Binarizer就是根据阈值进行二值化,大于阈值的为1.0,小于等于阈值的为0.0
(1,34.0),
(2,56.0),
(3,58.0),
(4,23.0)
转化过后为
---+----+-----------------+
| id| age|binarized_feature|
+---+----+-----------------+
| 1|34.0| 0.0|
| 2|56.0| 1.0|
| 3|58.0| 1.0|
| 4|23.0| 0.0|
类别数据整数化 LabelEncoder
可以将数据(类别型或者数值型都可以)转换为一个整数值,比如讲高中低转换为0,1,2,假设特征的取值类别有n种,那么转换到的范围就是[0:n],LabelEncoder的输入必须是个一维的数组,如Series这种格式,如果是DataFrame则会报错,看个例子
df['B'] = ['a','b','c','d']
df
A B C
0 0 a 2
1 3 b 5
2 6 c 8
3 9 d 11
le = LabelEncoder()
le.fit_transform(df.A)
输出:array([0, 1, 2, 3])
le = LabelEncoder()
le.fit_transform(df.B)
输出:array([0, 1, 2, 3])
StandardScaler
作用:去均值和方差归一化。且是针对每一个特征维度来做的,而不是针对样本
对于同一个特征,不同的样本中的取值可能会相差非常大,一些异常小或异常大的数据会误导模型的正确训练;另外,如果数据的分布很分散也会影响训练结果。以上两种方式都体现在方差会非常大。此时,我们可以将特征中的值进行标准差标准化,即转换为均值为0,方差为1的正态分布。如果特征非常稀疏,并且有大量的0(现实应用中很多特征都具有这个特点),Z-score 标准化的过程几乎就是一个除0的过程,结果不可预料。所以在训练模型之前,一定要对特征的数据分布进行探索,并考虑是否有必要将数据进行标准化。基于特征值的均值(mean)和标准差(standard deviation)进行数据的标准化。它的计算公式为:标准化数据=(原数据-均值)/标准差。标准化后的变量值围绕0上下波动,大于0说明高于平均水平,小于0说明低于平均水平
模型评估之混淆矩阵
在前面的文章中我们讲到了回归模型和分类模型的评估指标,区分了准确率和精确率的区别,并且比较了精确率和召回率内在的联系。本篇文章我们再来学习另外一个评估方法,即混淆矩阵(confusion_matrix)。
在讲矩阵之前,我们先复习下之前在讲分类评估指标中定义的一些符号含义,如下:
- TP(True Positive):将正类预测为正类数,真实为0,预测也为0
- FN(False Negative):将正类预测为负类数,真实为0,预测为1
- FP(False Positive):将负类预测为正类数, 真实为1,预测为0
- TN(True Negative):将负类预测为负类数,真实为1,预测也为1
混淆矩阵定义及表示含义
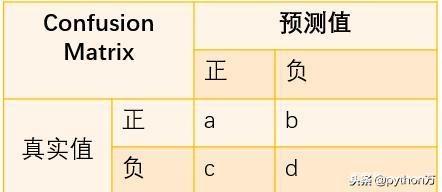
混淆矩阵是机器学习中总结分类模型预测结果的情形分析表,以矩阵形式将数据集中的记录按照真实的类别与分类模型预测的类别判断两个标准进行汇总。其中矩阵的行表示真实值,矩阵的列表示预测值,下面我们先以二分类为例,看下矩阵表现形式,如下:
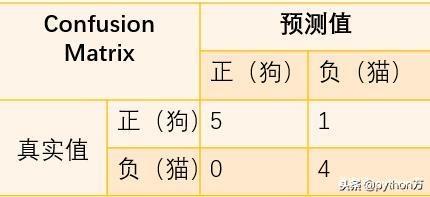
现在我们举个列子,并画出混淆矩阵表,假如宠物店有10只动物,其中6只狗,4只猫,现在有一个分类器将这10只动物进行分类,分类结果为5只狗,5只猫,那么我们画出分类结果混淆矩阵,并进行分析,如下(我们把狗作为正类):
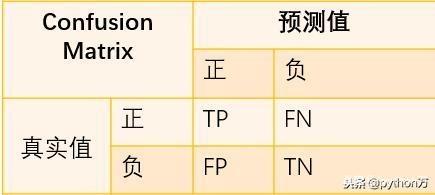
通过混淆矩阵我们可以轻松算的真实值狗的数量(行数量相加)为6=5+1,分类得到狗的数量(列数量相加)为5=5+0,真实猫的数量为4=0+4,分类得到猫的数量为5=1+4。同时,我们不难发现,对于二分类问题,矩阵中的4个元素刚好表示TP,TN,FP,TN这四个符号量,如下图:
那么对于二分类问题来说,精确率Precision=a/(a+c)=TP/(TP+FP),召回率recall=a/(a+b)=TP/(TP+FN),准确率accuracy=(a+d)/(a+b+c+d)=(TP+FN+FP+TN),可以看到准确率中的分子值就是矩阵对角线上的值。
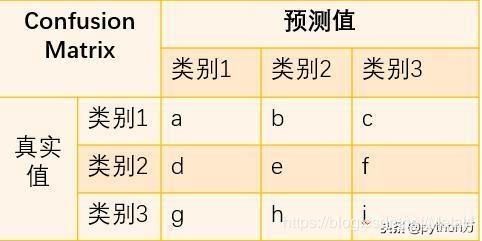
刚才分析的是二分类问题,那么对于多分类问题,混淆矩阵表示的含义也基本相同,这里我们以三类问题为例,看看如何根据混淆矩阵计算各指标值。
与二分类混淆矩阵一样,矩阵行数据相加是真实值类别数,列数据相加是分类后的类别数,那么相应的就有以下计算公式;
精确率_类别1=a/(a+d+g)
召回率_类别1=a/(a+b+c)
Python代码实现混淆矩阵
Python中的sklearn库提供了相应的方法来输出矩阵数据,非常方便,函数如下:
sklearn.metrics.confusion_matrix(y_true, y_pred, labels=None, sample_weight=None)
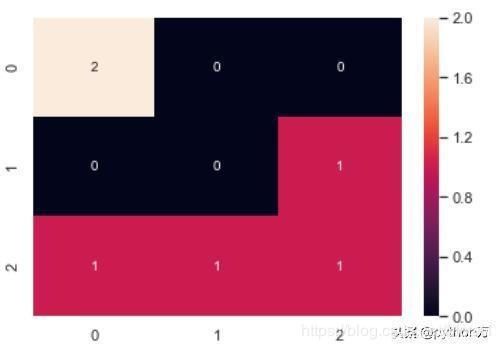
其中,y_true:是样本真实分类结果,y_pred 是样本预测分类结果 ,labels是所给出的类别,通过这个可对类别进行选择 ,sample_weight 是样本权重。这里我们用代码演示三分类问题混淆矩阵(这里我们用confusion_matrix生成矩阵数据,然后用seaborn的热度图绘制出混淆矩阵数据),如下:
#导入依赖包
import seaborn as sns;from sklearn.metrics
import confusion_matrix
import matplotlib.pyplot as pltsns.set()
y_true = ["cat", "dog", "cat", "cat", "dog", "rebit"]
y_pred = ["dog", "dog", "rebit", "cat", "dog", "cat"]
C2= confusion_matrix(y_true, y_pred, labels=["dog", "rebit", "cat"])
sns.heatmap(C2,annot=True)