零钱兑换Ⅰ和Ⅱ的标准解法

最近看题，动态规划似乎解题模板都差不多，多次碰到零钱兑换类的题目，遂总结一二

零钱兑换

题图如下所示，意思比较明朗，总共amount=11，现有面额1，2，5的coin，求凑成amount所花费的最少coins。

这道题，很容易想到公式 f(11) = min( f(11-1), f(11-2), f(11-5) )+1； 所以简单的状态转移方程为：dp [i] = min( dp[i], dp[i-coins[j]] +1) 初始化的dp[0]=0

因为 需要花费最多的coins 是这种情况 countMax = amount / min(coins[i]) ,
在这一题中，amount = 11, min(coins[i[) = 1,所以极端情况下，countMax = 11/1=11，所以dp填充的数值需要大于countMax。

我们由上面的状态转移方程可以很轻松的写出如下程序：
解题模板

class Solution {
    public int coinChange(int[] coins, int amount) {
    	if(coins.length==0)
    		return -1;
    	int dp[]=new int[amount+1];
    	Arrays.fill(dp,amount+1);
    	dp[0]=0;
    	for(int i=0;i<=amount;i++){
    		for(int j=0;j<coins.length;j++){
    			if(i>=coins[j]){
    				dp[i] = Math.min(dp[i],dp[i-coins[j]]+1);
    			}
    		}
    	}
    	return dp[amount]==amount+1?-1:dp[amount];
    }
}

零钱兑换Ⅰ这个题目，其实可以转变为很多类似的题目，比如说：

现有amount级台阶，你可以选择coins = {1,2,5} 一次跳跃的台阶级数，求到达amount级台阶，你需要花费最少的跳跃次数。不过需要关注顺序问题。

这道题完全可以复用上述的解法，只需要改变一下for循环的顺序即可，因为这里的核心问题都是一个，现在有一个 总的amount，以及可选一次所花费的代价coins[] , 求到达总的amout需要最少的代价。

零钱兑换Ⅱ

这道题的初始化条件和上题是一致的，只是需要求解条件的结果不同，需要求解用coins可以组合amount的总的组合数量。

按照题意，可以想到公式：sum(n)+ = f(n-coins[j])
可以得出状态转移方程： dp[i] = dp[i] + dp[i-coins[j] , 初始化的dp[0]=1
解题模板

class Solution {
    public int change(int amount, int[] coins) {
    	int dp[]=new int[amount+1];
    	dp[0]=1;
    	for(int i:coins){
    		for(int j=i;j<=amount;j++){
    			dp[j]+=dp[j-i];
    		}
    	}
    	return dp[amount];
    }
}

零钱兑换Ⅱ这个题目，也可以延伸到其他类似的题目，以台阶为例，存在amount级台阶，每一次可以跳 coins[]={1,2,5}级台阶，求通过amount级台阶的跳法总数。
这个有点类似于斐波那契的题目，斐波那契题目如下

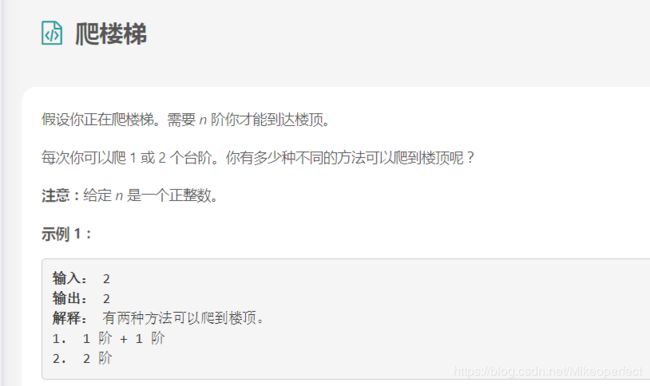
这里需要注意的地方就在于，爬楼梯是有顺序的，而零钱兑换则是无顺序的，所以爬楼梯是排列问题，而零钱兑换是组合问题，所以类似题型解题模板如下：
排列问题解题模板
主要用于爬楼梯等需要顺序的问题

class Solution {
    public int climbStairs(int n) {
        int coins[]=new int[]{1,2};
        int dp[]=new int[n+1];
        dp[0]=1;
        for(int i=1;i<=n;i++){
            for(int j:coins){
                if(i>=j){
                    dp[i]+=dp[i-j];
                }
            }
        }
        return dp[n];
    }
}

组合问题解题模板
主要用于零钱兑换等无需顺序的问题

class Solution {
    public int change(int amount, int[] coins) {
    	int dp[]=new int[amount+1];
    	dp[0]=1;
    	for(int i:coins){
    		for(int j=i;j<=amount;j++){
    			dp[j]+=dp[j-i];
    		}
    	}
    	return dp[amount];
    }
}