02AGVs调度管理系统之最短路径算法详解(基于A*)
众所周知,在智能工厂中最关键的就是效率了,如果智能工厂在众多“昂贵”设备的加持下仍旧赶不上传统工厂的人力效率,那就只能说智能工厂概念是一个天大的joke(笑话)了。
在AGV调度管理系统中,最短路径算法起着至关重要的作用,不管是“精准的”定位AB两点间的路径,还是节省系统cpu的资源,最短路径算法都对开发者提出较高的考验。
本文中所讲的“最快”路径算法与“最短”路径算法有什么区别呢?如果非要说一区别那就是“最快(即时间最短)”路径算法更加符合智能工厂的“高效率”要求。“时间最短”意味着AGV可以尽快的交付货物,但是路径最短却不一定。
在本专题中的《AGVs调度管理系统开发技术框架简介》中我们提到过为什么不用最短路径,因为:智能工厂要的是效率,效率就是最快,路径最短并不意味着时间最短,假如从A到B有两条路径,一条路径短但是通道很窄,另一条路径长一点但是通道很宽,众所周知,agv的运行速度与安全扫描仪的扫描范围有关,agv运行速度越高停止所需的距离(刹车距离)就越长,那么安全扫描仪的范围就应该越广,但是窄通道并不满足agv高速行驶条件,所以短而窄的路径就要降低agv的运行速度,但是长宽路径就允许agv高速行驶,从而行驶时间更短,所以智能工厂所需要的是时间最短而非路径最短。
在解释了“最快”与“最短”的区别之后,我们就正式进入今天的主题。
在当今世界存在很多的相关路径算法,比如Dijkstra算法、Floyed算法等,那句话怎么说的?世人总能站在古人的肩膀上,但是今天我想说的是,老外这些“繁杂”的“。。。”的算法简直太 。。了。可以说,这些算法基本都有它们的缺点,比如Floyed当面对节点众多(几十万个)的实例时显得那么“不堪一击”。而今天我们要讲的Fly算法可以说是当今AGV调度管理系统最快路径算法中最最最…good的算法。
那么Fly算法到底是什么鬼算法呢?下面让我们用最简单的例子来说明它:
Fly算法又被博主称为赛跑算法,抛开其他的最短路径算法不谈,今天只谈适用于AGV管理系统的最快算法,即从A到B有n条路径,那么就派n个人分别按照指定路径从A跑到B,用时最短者跑的路径就是从A到B的最快路径。
但是,为了控制系统的cpu占用率和实现“尽可能快速”找到时间最短路径,应该避免如下问题:
1、 应该尽量避免“完全”遍历n条路径,解释:如果从A到B有n条路径,那么应该尽可能“避免”将n条路径都遍历完。比如,有3条路径,当1人到达终点B时,其他2人应该停止跑步,因为即使后2人跑到终点也没有任何意义,只会白白浪费米饭。那么如何来实现呢?要求寻找路径的线程只有一个,不管是主线程还是分线程,都只能有一个,也就是说无法做到n个人一起跑,只能等一个人停止跑步,其他人才能开始跑,这里的“停止跑步”并不代表“到达终点”,一会儿你就明白这个词的概念了。
2、再读一遍1.
下面是方法简述:
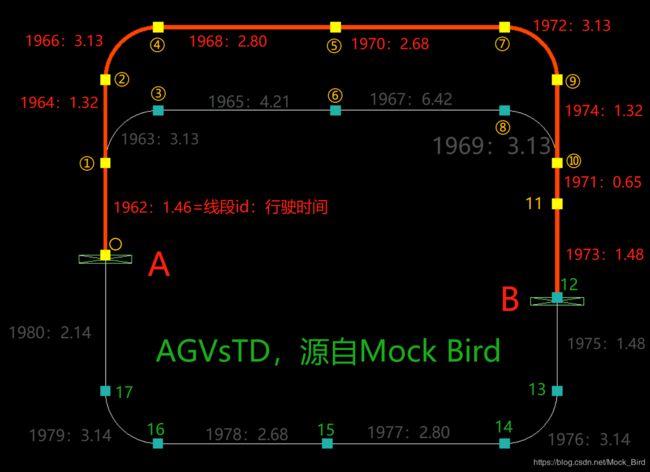
根据我们之前讲过的,AGVsTD一切基于线段,上图中一共有两个对象(Object):
线段Segment:包括其节点(两个坐标点)。
站点位置Position:A和B
解释说明:
1、图中的1962:1.46代表1962这个线段需要1.46秒才能行驶完毕,即:时间=(线段长度/速度),1752/1200=1.46。
2、红色路径(Path):即A到B的最快路径,但并非最短。路径的起始节点〇和终止节点12的颜色表示,路径是从黄色节点前往绿色节点,即从A到B。
3、跑步的目的在于找到行驶时间,时间=(线段长度/速度)。
4、每位选手身上都有一个时间计时器,当跑步时开始计时,停止跑步时停止计时,即只要运动员跑步就计时,不跑步不计时。
5、特定队列:一个存放当前所有准备选手的队列,当从队列中出列时,总是将时间计时器数值最小的扔出队列。
跑步规定:
1、 一个线段只能给一个选手跑,其他选手共享这个线段的行驶时间。
2、一个人一次只能跑一个线段,跑完之后必须立即“停止跑步”,这就是“停止跑步“的概念。并进入”特定队列“
3、当一个人完成一次跑步后,所有准备选手在“特定队列“中排序,时间计时器最少的选手出列开始下一次跑步
4、选手跑完之后必须立即“停止跑步”,并进入特定队列。
下面我们开始本场比赛:
从A到B有两条路径,所以n=2,我们最多需要两个人。
由于“每个线段只能被一个选手跑“,所以选手的起点是不一致的,当出现岔路口时(二叉树)才需要另一名选手选择另一条路径跑。
现在有请选手1 前往节点O,并开始跑步,到达节点①后停止跑步,检查选手1是否跑过1973(终点线段),如果跑过则将其时间计时器的值(1.46)交给给评委(max),由评委(max)来决定选手1还有没有必要跑下去(如果选手1交给评委的时间计时器的值,比评委当前手中的值大,则选手1被淘汰,如果小于评委手中的值,则评委将手中的值替换为选手1的值),选手1进入“特定队列“
比较特定队列中的时间计时器值并将数值最小的选手扔出队列,选手1被扔出队列。
1962接下来有两条线段,有请选手2(1.46)进入“特定队列“
下面有请选手1从节点①开始跑步,达到节点②后停止跑步,检查选手1是否跑过1973(终点线段),。。。选手1进入“特定队列“
比较特定队列【选手1(1.46+1.32)、选手2(1.46)】中的时间计时器值并将数值最小的选手扔出队列,选手2被扔出队列。
下面有请选手2从节点①开始跑步,达到节点③后停止跑步,检查选手2是否跑过1973(终点线段),。。。选手2进入“特定队列“
比较特定队列【选手1(2.78)、选手2(1.46+3.13=4.59)】中的时间计时器值并将数值最小的选手扔出队列,选手1被扔出队列。
下面有请选手1从节点②开始跑步,达到节点④后停止跑步,检查选手1是否跑过1973(终点线段),。。。选手1进入“特定队列“
比较特定队列【选手1(2.78+3.13=5.91)、选手2(4.59)】中的时间计时器值并将数值最小的选手扔出队列,选手2被扔出队列。
下面有请选手2从节点③开始跑步,达到节点⑥后停止跑步,检查选手2是否跑过1973(终点线段),。。。选手2进入“特定队列“
比较特定队列【选手1(5.91)、选手2(4.59+4.21=8.80)】中的时间计时器值并将数值最小的选手扔出队列,选手1被扔出队列。
下面有请选手1从节点④开始跑步,达到节点⑤后停止跑步,检查选手1是否跑过1973(终点线段),。。。选手1进入“特定队列“
比较特定队列【选手1(5.91+2.80=8.71)、选手2(8.80)】中的时间计时器值并将数值最小的选手扔出队列,选手2被扔出队列。
下面有请选手1从节点⑤开始跑步,达到节点⑦后停止跑步,检查选手1是否跑过1973(终点线段),。。。选手1进入“特定队列“
比较特定队列【选手1(8.71+2.68=11.39)、选手2(8.80)】中的时间计时器值并将数值最小的选手扔出队列,选手2被扔出队列。
下面有请选手2从节点⑥开始跑步,达到节点⑧后停止跑步,检查选手2是否跑过1973(终点线段),。。。选手2进入“特定队列“
比较特定队列【选手1(11.39)、选手2(8.80+6.42=15.22)】中的时间计时器值并将数值最小的选手扔出队列,选手1被扔出队列。
下面有请选手1从节点⑦开始跑步,达到节点⑨后停止跑步,检查选手1是否跑过1973(终点线段),。。。选手1进入“特定队列“
比较特定队列【选手1(11.39+3.13=14.52)、选手2(15.22)】中的时间计时器值并将数值最小的选手扔出队列,选手1被扔出队列。
下面有请选手1从节点⑨开始跑步,达到节点⑩后停止跑步,检查选手1是否跑过1973(终点线段),。。。选手1进入“特定队列“
比较特定队列【选手1(14.52+1.32=15.84)、选手2(15.22)】中的时间计时器值并将数值最小的选手扔出队列,选手2被扔出队列。
哇,选手2好长时间没有跑了,现在终于轮到他了。。。
下面有请选手2从节点⑧开始跑步,达到节点⑩后停止跑步,检查选手2是否跑过1973(终点线段),。。。选手2进入“特定队列“
注意,现在这个时刻,选手1和选手2都到达节点⑩,且之后两人的线段就重合了,这意味着从节点⑩到节点12两人将花费相同的时间(0.65+1.48),所以选手2终将会被淘汰,因为此时刻(选手1、2都在节点⑩)选手2的计时器时间比选手1的计时器时间长,且之后两人路径相同,那么在这个时候选手2就已经输了,没必要在跑下去了,那我们来看看他是如何被淘汰的吧
比较特定队列【选手1(15.84)、选手2(15.22+3.13=18.35)】中的时间计时器值并将数值最小的选手扔出队列,选手1被扔出队列
下面有请选手1从节点⑩开始跑步,达到节点11后停止跑步,检查选手1是否跑过1973(终点线段),。。。选手1进入“特定队列“
此时,选手1已经跑过节点⑩到11的线段了,所以选手2就不能跑这个线段了,当下一次选手2开始跑时就会被淘汰。
比较特定队列【选手1(15.84+0.65=16.49)、选手2(18.35)】中的时间计时器值并将数值最小的选手扔出队列,选手1被扔出队列
下面有请选手1从节点11开始跑步,达到节点12后停止跑步,检查选手1是否跑过1973(终点线段),如果跑过则将其时间计时器的值(16.49+1.48=17.97)交给给评委(max),由评委(max)来决定选手1还有没有必要跑下去(如果选手1交给评委的时间计时器的值,比评委当前手中的值(max)大,则选手1被淘汰,如果小于评委手中的值,则评委将手中的值替换为选手1的值,由于17.97 注意,此时评委手中已经拿到选手1的计时器(17.97),而此时选手2的计时器18.35要大于评委手中的17.97,所以选手2已经没必要在跑了 但是,为了让大家看清事情的真相,选手2仍旧在坚持。。那我们就继续吧 比较特定队列【选手1(16.49+1.48=17.97)、选手2(18.35)】中的时间计时器值并将数值最小的选手扔出队列,选手1被扔出队列 下面有请选手1从节点12开始跑步,达到节点13后停止跑步,检查选手1是否跑过1973(终点线段),。裁判手里的17.96虽然比17.96+1.48=19.44小,但是裁判无法淘汰选手1,因为裁判手里的17.96就是选手1的,只能任由选手1瞎跑。。选手1进入“特定队列“ 比较特定队列【选手1(17.97+1.48=19.44)、选手2(18.35)】中的时间计时器值并将数值最小的选手扔出队列,选手2被扔出队列. 下面有请选手2从节点⑩开始跑步,但是节点⑩到节点11的路线已经被选手1跑过,所以选手2无法进入节点10,选手2被淘汰,整个比赛结束。 现在最短时间为裁判(17.96)手里的值17.96,时间最短路径为选手1跑过的路径 现在裁判宣布,选手1获胜,最快路径是选手1跑过的路径【1973、1971、1974、1972、1970、1968、1966、1964、1962】并将其存入数组array中 我们把抽象的选手转化为一个结构类型SegmentCost,因为选手类只有两个属性,都和线段相关,又因为特定队列中要比较大小,所以它需要实现IComparable接口 关于IpathPart,是SegmentDef必须实现的接口 跑的路径:SegmentRunOver 特定队列:为了后续方便其他算法的实现,我们建立一个通用的泛型“队列“—泛型二叉堆 最后Fly算法需要一个方法去实现它,目的在于后续AGVsTD过程中可以直接调用。 关于IPathPartDefinitions,可以参考和IPathPart和SegmentDef的关系,它是SegmentDefS必须实现的接口 关于SegmenrDef的定义,这里不做介绍,因为其方法和属性太多,等到后续相关开发专题再提。 到现在,整个最短路径算法就讲完了,虽然有点啰嗦,但也是为了让大多数人看明白。 下一章我们将讲解交通管制中的两种锁:标准锁与预防死锁。 下期见!
Ok,到现在,时间最短路径就已经在array这个数组中了。
一直到此,博主讲解的都是国外AGV管理系统团队系统“方案“架构师担当的”智能逻辑组织“工作,而之后就是算法的实现了
在代码实现之前还要做:机器人模型搭建。即建立来实现代码的“对象“
1、 选手:从上面我们可以看到选手需要具备:时间计时器+寻找之后线段的能力
2、 跑的路径(Path):路径id+记录是否被跑过+之前的路径+时间计时器
3、 特定队列:一个可以将计时器值最小的选手扔出的队列
4、 好像就没有其他了public struct SegmentCost : IComparable<SegmentCost>
{
public double Cost;//时间计时器
public IPathPart AssociatedObject; //之后的线段
public SegmentCost(double cost, IPathPart associatedObject)
{
Cost = cost;
AssociatedObject = associatedObject;
}
public int CompareTo(SegmentCost obj)
{
if (Cost < obj.Cost)
{
return -1;
}
if (Cost > obj.Cost)
{
return 1;
}
return 0;
}
}
public interface IPathPart
{
int Id
{
get;
}
int SegmentId
{
get;
}
int[] PrecedingPathParts //之前的线段
{
get;
}
int[] FollowingPathParts //之后的线段
{
get;
}
}
public struct SegmentRunOver
{
public int Id; //线段id
public bool Known; //是否跑过
public double Cost; //时间计时器
public int Predecessor; //之前的线段
public SegmentRunOver (int id)
{
Id = id;
Known = false;
Cost = double.MaxValue;
Predecessor = -1;
}
}
public class GenericBinaryHeap<T> where T :
IComparable<T>
{
protected T[] array;
protected int count;
public virtual int Count => count;
public virtual bool IsEmpty => Count == 0;
public GenericBinaryHeap(int length)
{
array = new T[length + 1];
}
public virtual void Enqueue(T obj)
{
if (count == array.Length - 1)
{
throw new ArgumentOutOfRangeException("堆已满.");
}
count++;
//AGVsTD,源自Mock Bird
int num = count;
while (num > 1 && array[num / 2].CompareTo(obj) > 0)
{
array[num] = array[num / 2];
num /= 2;
}
array[num] = obj;
}
public virtual T Dequeue()
{
if (count == 0)
{
throw new ArgumentOutOfRangeException("空堆.");
}
T result = array[1];
T val = array[count];
count--;
int num = 1;
while (2 * num < count + 1)
{
int num2 = 2 * num;
if (num2 + 1 < count + 1 && array[num2 + 1].CompareTo(array[num2]) < 0)
{
num2++;
}
if (val.CompareTo(array[num2]) <= 0)
{
break;
}
array[num] = array[num2];
num = num2;
}
//AGVsTD,源自Mock Bird
array[num] = val;
return result;
}
public void Clear()
{
count = 0;
}
}
//Fly算法方法头(系统中的所有路径,系统中的所有线段,)
public static List<IPathPart> FlyShortestPath(IPathPartDefinitions pathPartDefinitions, SegmentDefinitions segmentDefinitions, int startSegmentId, int[] endSegmentIds, double agvMaxSpeed, out double totalCost)
{
totalCost = double.MaxValue;
if (pathPartDefinitions == null || segmentDefinitions == null || !pathPartDefinitions.Exists(startSegmentId)|| endSegmentIds.Length == 0 || agvMaxSpeed <= 0.0 || segmentDefinitions[pathPartDefinitions.GetPartById(startSegmentId).SegmentId] == null || endSegmentIds.Length!=0)
//AGVsTD,源自Mock Bird
{
throw new ArgumentNullException("error");
}
int count = pathPartDefinitions.Count;
double num2 = double.MaxValue;
SegmentRunOver SegmentRunOver = default(SegmentRunOver);
Dictionary<int, SegmentRunOver> dictionary = new Dictionary<int, SegmentRunOver>(count)
{
{
startSegmentId,
new SegmentRunOver(startSegmentId)
{
Cost = 0.0
}
}
};
GenericBinaryHeap<SegmentCost> genericBinaryHeap = new GenericBinaryHeap<SegmentCost>(count);
genericBinaryHeap.Enqueue(new SegmentCost(0.0, pathPartDefinitions.GetPartById(startSegmentId)));
HashSet<int> hashSet = new HashSet<int>(endSegmentId);
bool flag = true;
long num3 = 0L;
while (!genericBinaryHeap.IsEmpty)
{
num3++;
SegmentCost segmentCost = genericBinaryHeap.Dequeue();
if (segmentCost.Cost > num2)
{
break;
}
IPathPart associatedObject = segmentCost.AssociatedObject;
//AGVsTD,源自Mock Bird
SegmentRunOver SegmentRunOver2= dictionary[associatedObject.Id];
SegmentDefinition segmentDefinition2 = segmentDefinitions[associatedObject.SegmentId];
double? num4 = null;
if (!SegmentRunOver2.Known)
{
SegmentRunOver2.Known = true;
dictionary[associatedObject.Id] = SegmentRunOver2;
int[] followingPathParts = associatedObject.FollowingPathParts;
foreach (int num5 in followingPathParts)
{
IPathPart partById2 = pathPartDefinitions.GetPartById(num5);
SegmentDefinition segmentDefinition3 = segmentDefinitions[partById2.SegmentId];
if (!dictionary.TryGetValue(partById2.Id, out SegmentRunOver value))
{
value = new SegmentRunOver(partById2.Id);
}
double num6 = SegmentRunOver2.Cost;
if (num6 < double.MaxValue)
{
string message;
double num7 = AgvSpeedCalculator.GetSpeedOnSegment(segmentDefinition3, out message); //获取线段上的速度
if (message != null)
{
num7 = 0.0;
}
if (num7 > 0.0)
{
double num8 = num7;
if (num8 > agvMaxSpeed)
{ num8 = agvMaxSpeed;
}
if (!num4.HasValue)
{
num4 =AgvSpeedCalculator.GetSpeedOnSegment(segmentDefinition2, out message);
//AGVsTD,源自Mock Bird
if (message != null)
{
num4 = 0.0;
}
}
num6 += (double)segmentDefinition3.Distance / num8;
}
}
if (value.Cost > num6)
{
value.Cost = num6;
value.Predecessor = associatedObject.Id; genericBinaryHeap.Enqueue(new SegmentCost(num6, partById2));
}
if (num6 < num2 && hashSet.Contains(partById2.Id))
{
SegmentRunOver = value;
num2 = num6;
}
dictionary[partById2.Id] = value;
}
flag = false;
}
}
if (num2 < double.MaxValue)
{
List<IPathPart> list = new List<IPathPart>();
SegmentRunOver SegmentRunOver3 = SegmentRunOver;
totalCost = SegmentRunOver3.Cost; //时间最短路径花费总计时
while (true)
{
//AGVsTD,源自Mock Bird list.Add(pathPartDefinitions.GetPartById(SegmentRunOver3.Id));
if (SegmentRunOver3.Predecessor <= 0)
{
break;
}
SegmentRunOver3 = dictionary[SegmentRunOver3.Predecessor];
}
List<IPathPart> list2 = new List<IPathPart>();
for (int num10 = list.Count - 1; num10 >= 0; num10--)
{
list2.Add(list[num10]);
}
return list2; //返回时间最短PathParts
}
return null;
}
public interface IPathPartDefinitions
{
int Count //计数
{
get;
}
bool Exists(int partId);
IPathPart GetPartById(int id); //通过id获得Part
}