计算机图形学——OPENGL应用
计算机图形学——OPENGL多边形填充
一 实验目的
通过实践对多边形填充算法有更充分的认识,让同学们上完计算机图形学这门课之后都不是仅仅停留在理论,通过自己动手对opengl,c++都有更好的使用,同时也为我们打开了新世界的大门。帮助我们学习计算机图形学的知识。
二 实验内容
1 OpenGL 实现
2 通过橡皮筋交互输入多边形
3 清屏重置多边形
4 多边形扫描算法中的顶点处理以每条边减去一个像素方法处理
5 要类(或模版类)来表示数据结构
6 多文档组织,至少要用头(.h)文件表示数据结构
7 通过菜单交互
8 自相交多边形、多个多边形的扫描填充
9 通过文件存储和读出已经交互输入的多边形
三 算法实现
. 1. 活性边表的具体变化过程
“活动边表”是扫描线填充算法的核心,整个算法都是围绕着这张表进行处理的。要完整的定义“活动边表”,需要先定义边的数据结构。每条边都和扫描线有个交点,扫描线填充算法只关注交点的x坐标。每当处理下一条扫描线时,根据△x直接计算出新扫描线与边的交点x坐标,可以避免复杂的求交计算。一条边不会一直待在“活动边表”中,当扫描线与之没有交点时,要将其从“活动边表”中删除,判断是否有交点的依据就是看扫描线y是否大于这条边两个端点的y坐标值,为此,需要记录边的y坐标的最大值。根据以上分析,边的数据结构可以定义如下:
//“活动边表(AET)”和“新边表(NET)”
typedef struct XET {
float x;
float dx, ymax;
XET* next;
}AET, NET;

A(288,769) B(293,530) C(714,784) D(734,506)
图(1) 多边形与扫描线示意图
扫描线算法的核心就是围绕“活动边表(AET)”展开的,为了方便活性边表的建立与更新,我们为每一条扫描线建立一个“新边表(NET)”,存放该扫描线第一次出现的边。当算法处理到某条扫描线时,就将这条扫描线的“新边表”中的所有边逐一插入到“活动边表”中。“新边表”通常在算法开始时建立,建立“新边表”的规则就是:如果某条边的较低端点(y坐标较小的那个点)的y坐标与扫描线y相等,则该边就是扫描线y的新边,应该加入扫描线y的“新边表”。 图(1)所示多边形中各扫描线的“新边表”如下图所示:
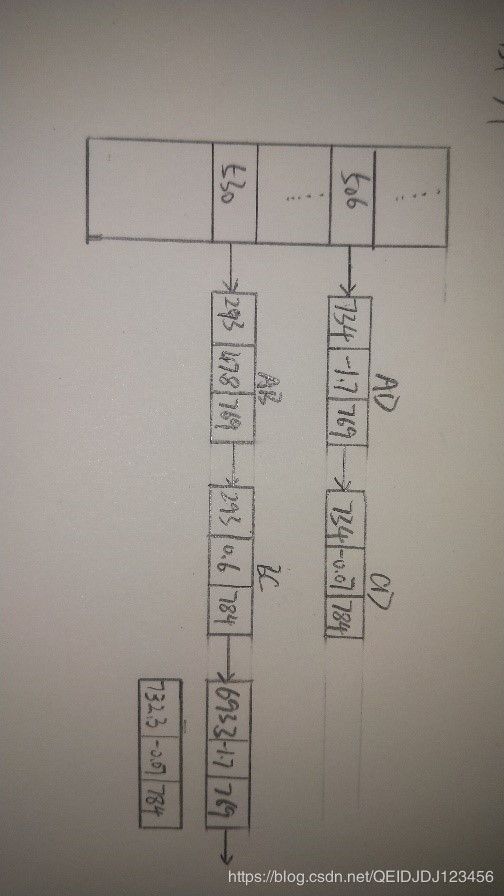
图(2) 各扫描线的新边表
然后对边表进行排序,具体实现代码见下面功能模块。
四 实验结果
-
通过橡皮筋交互输入多边形
通过橡皮筋交互输入相应的多边形,鼠标左键为输入点,右键为结束划线(大于两个点,否则撤销输入),最后一点与开始的点连线形成多边形。

图(3)橡皮筋输入的多边形 -
对输入的多边形进行填充
在交互输入多边形的过程中,把相应点的坐标存放到多边形结构体中,然后将多边形在算法中扫描建立NET表,然后进行排序,最后将其填充。

图(4)填充之后的多边形
算法步骤:
1.首先对输入的多边形求出最高点和最低点,减少扫描线扫描的次数,提高计算速度。vector polypoint = s.p;
int POINTNUM = polypoint.size();
int MinY=1000, MaxY = 0;//扫描开始,结束的位置
for (int i = 0; i < POINTNUM; i++) {
if (polypoint[i].y > MaxY) {
MaxY = polypoint[i].y;
}
if (polypoint[i].y < MinY) {
MinY = polypoint[i].y;
}
}
2.预先初始化NET,AET,原理上讲,填充的时候是根据活性边表AET进行填充的,但是活性边表AET的更新又是依据边表NET。然后自上而下扫描并建立NET。
for (int i = MinY; i < MaxY; i++) {
for (int j = 0; j < POINTNUM; j++) {
if (polypoint[j].y == i) {
/*前面的那个点*/
if (polypoint[(j - 1 + POINTNUM) % POINTNUM].y > polypoint[j].y) {
NET* p = new NET;
p->x = polypoint[j].x;
p->ymax = polypoint[(j - 1 + POINTNUM) % POINTNUM].y;
p->dx = (polypoint[(j - 1 + POINTNUM) % POINTNUM].x - polypoint[j].x) / (polypoint[(j - 1 + POINTNUM) % POINTNUM].y - polypoint[j].y);//斜率的倒数
p->next = pNET[i]->next;
pNET[i]->next = p;
}
/*后面的那个点*/
if (polypoint[(j + 1 + POINTNUM) % POINTNUM].y > polypoint[j].y) {
NET* p = new NET;
p->x = polypoint[j].x;
p->ymax = polypoint[(j + 1 + POINTNUM) % POINTNUM].y;
p->dx = (polypoint[(j + 1 + POINTNUM) % POINTNUM].x - polypoint[j].x) / (polypoint[(j + 1 + POINTNUM) % POINTNUM].y - polypoint[j].y);
p->next = pNET[i]->next;
pNET[i]->next = p;
}
}
}
}
- 计算新的交点x,更新AET。更新完以后,对活性边表AET按照x值从小到大排序。
NET* p = pAET->next;
while (p) {
p->x = p->x + p->dx;
p = p->next;
}
//更新完以后,对活性边表AET按照x值从小到大排序
AET* tq = pAET;
p = pAET->next;
tq->next = NULL;
while (p) {
while (tq->next && p->x >= tq->next->x)//重新排序
tq = tq->next;
NET * s = p->next;
p->next = tq->next;
tq->next = p;
p = s;
tq = pAET;
}
4.顶点处理,删除y=ymax的节点,避免出现奇顶点。
AET* q = pAET;
p = q->next;
while (p) {
if (p->ymax == i) {
q->next = p->next;
delete p;
p = q->next;
}
else {
q = q->next;
p = q->next;
}
- 将NET中的新点加入AET,并用插入法按x递增排序
p = pNET[i]->next;
q = pAET;
while (p) {
while (q->next && p->x >= q->next->x)
q = q->next;
NET * s = p->next;
p->next = q->next;
q->next = p;
p = s;
q = pAET;
}
p = pAET->next;
- 改写像素的颜色值
while (p && p->next) {
for (float j = p->x; j <= p->next->x; j++) {
glColor3f(1.0, 0.0, 0.0);//填充颜色
glVertex2i(static_cast(j), i);
}
p = p->next->next;////考虑端点情况
}
- 自相交多边形、多个多边形的扫描填充
循环调用一个多边形的填充方法即可,下图中五角星中间为空,是因为填充时,按照排序后的边表进行填充的,每一个扫描线对应填充的点是1和2,3和4……之间的空白区域,故刚好中间为空。


图(5)自相交多边形及填充 图(6)多个多边形输入及填充
主要代码为:
if (!s.empty())
{
for (i = 0; i < s.size(); i++) //对多边形类向量循环,该向量中的每个元素代表一个多边形
{
GLfloat a = s[i].red, b = s[i].green, c = s[i].blue;
glColor3f(a, b, c);
int k = s[i].p.size(); //将一个多边形的点的个数
for (j = 0; j < k; j++) //画多边形
{
glBegin(GL_LINES); //将当前的点与后一个点连线
glVertex2i(s[i].p[j].x, s[i].p[j].y);
glVertex2i(s[i].p[(j + 1) % k].x, s[i].p[(j + 1) % k].y);//,通过取模操作来避免越界问题,该思路来源于循环队列.
glEnd();
}
PolygonScanning (s[i]);
}
}
. 4. 通过文件存储和读出已经交互输入的多边形
首先通过橡皮筋算法画出多边形时,将该多边形所有的点集放入一个多边形,然后进行填充。然后继续画图,都放入多边形集中,这样保存所有已画多边形数据到多边形集中
,循环调用填充函数进行填充,之后然后显示出来。


图(7)画出的多边形 图(8)txt文件中保存的信息
实现一个循环,将多个多边形点集写入文件中,具体代码为:
/将已经画好了的多边形保存到文件中/
void SavePolygon()
{
int polygonnum = s.size();//获得多边形的数量,着一保存
ofstream out;//文件输出流
out.open("data.txt");
if (!out.is_open())//不存在该文件时
cout << "error:不存在该文件,无法打开!" << endl;
else
for (int i = 0; i < polygonnum; i++)
{
polygon poly = s[i];
int pointsize = poly.p.size();
for (int j = 0; j < pointsize; j++)
out << poly.p[j].x << "," << poly.p[j].y << " ";//多边形点与点之间用空格间隔开
out << endl;//当一个多边形输入完毕,换行输入下一个多边形
}
out.close();
cout << "成功保存多边形! " << endl;
}
从txt文件中按行读取相应点的坐标,我自己写了一个分割函数,将字符串按照输入的字符进行分割。分割之后,循环将每行得到的点集将放进一个多边形。将获得的多边形集,循环调用填充函数将所有的多边形都显示出来。


图(9)txt文件中保存的信息 图(10)读取、填充之后的多边形
//根据指定字符对字符串进行分割,从而能从文件中得到所需要的坐标值,返回的是一个存放分割后的每一个字符串矢量容器
vector SplitString(string srcStr, const string& delim)
{
int nPos = 0;
vector vec;
nPos = srcStr.find(delim.c_str());
while (-1 != nPos)
{
string temp = srcStr.substr(0, nPos);
vec.push_back(temp);
srcStr = srcStr.substr(nPos + 1);
nPos = srcStr.find(delim.c_str());
}
vec.push_back(srcStr);
return vec;
}
/载入上次画好的多边形/
void ReadPolygon() {
ifstream in("data.txt");
string bufline;//保存从文件中读出的字符串
if (!in.is_open())
cout << "Error:无法打开该文件!"< line = SplitString(bufline, " ");//根据空格识别每个点的坐标
for (int i = 0; i < line.size() - 1; i++)
{
point ppp;
vector tempString = SplitString(line[i], ",");
ppp.x = atoi(tempString[0].c_str());
ppp.y = atoi(tempString[1].c_str());
poly.p.push_back(ppp);
}
s.push_back(poly);
poly.p.clear();//清除p中信息
}
}
//从文件中读出多边形,然后进行赋值显示
for (int i = 0; i < s.size(); i++)
PolygonScanning(s[i]);
//s.push_back(temp[i]);
in.close();
glFlush();
cout << "成功读取多边形文件!"< 5. 清屏重置多边形
将屏幕上所有的多边形都清除,以及多边形的点集,多边形。刚开始实现清除函数的时候,总是需要点一下屏幕然后才能屏幕清空,不知道为什么,后来改了算法,按照扫描线那样,一行一行的清空屏幕,然后把多边集全部清空,否则下次刷新时仍会出现已经消失的多边形。


图(11)清空之前的图形 图(12)清空之后的屏幕
具体代码为:
void myClean() {
glClearColor(1.0f, 1.0f, 1.0f, 0.0f);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glBegin(GL_LINE_LOOP);
for (int i = 0; i <= 1000; i++) {
glVertex2f(0.0, 1000.0);
}
p.clear();
s.clear();//避免出现遗留
glEnd();
glFlush();
}
6. 通过菜单交互
原本是打算做一个菜单的,后来感觉用键盘交互一个道理,所以就做了用键盘交互(改进之后做了菜单)。将键盘几个固定键绑定函数,点击相应按键的时候,就会调用相应的函数来实现特殊的功能。(建议读者能尝试自己动手做一下菜单)
r表示read,从文件中读出多边形顶点集
s表示save,将多边形的顶点集写到文件中
c表示clear,将屏幕显示的所有多边形都删除,还有多边形的顶点集以及多边形。
具体代码为:
void keyboard(unsigned char key, int x, int y) {
switch (key)
{
case 's'|'S':
cout << "save" << endl;
SavePolygon();//保存多边形到txt文件中
break;
case'c'|'C':
cout << "clean" << endl;
myClean();//清除屏幕所有多边形
break;
case 'r'|'R':
ReadPolygon();//读出存入的多边形
break;
}
}
五 总结与体会
本例还有很多可以改进的地方,可以添加多边形的颜色,把多边形的颜色也写入多边形的结构体,这样保存(读出)的时候也可以保存(读出)多边形的颜色,还可以增加多种填充模式,比如等间隔、斜扫描线填充。最后,这是我第一次发布博客,做的不好的地方希望大家在评论里提些意见。希望大家能一起学习进步。
附:源码(仅供参考)