OFDM专题之子载波间干扰问题(一)
这个问题,拖到了今天,在一个星期之前我就一直紧张地看着,这是我的自由时间,然后为了考试,我停下了思考这部分内容,也没搞懂为什么子载波间为什么会有干扰,也查了网上的说法,基本没有直言面对的,大多数是说如何消除子载波间干扰,这就默认了子载波间存在干扰,当然,可能是因为这个内容十分简单,大家都明白。可我认为我有必要说说这个问题,个人感觉只有明白产生的原因,解决方法也就容易多了,否则就会云里雾里,让人困惑不已。
进入正题:
上篇博文讲了多径效应引起的码间串扰问题,也就是码元之间的干扰问题,也叫符号间的干扰,都是一个意思。见博文:
多径效应引起的码间串扰
上篇博文的前提是为了简单地理解多径引起的码间串扰,所以假设信号波形是基带信号,且接收端是通过采样判决来恢复信号的,这篇博文不同,它是实实在在地应用在OFDM系统之中。
也就是本博文的前提,假设多径是两个径,即路径1与路径2,以便于分析,同样存在多经时延,且最大时延为符号间保护间隔的长度,这也算是最大时延长度了。
下面就按部就班的来吧。
第一个问题:(铺垫内容)
OFDM符号时长与子载波间频率间隔之间的关系?
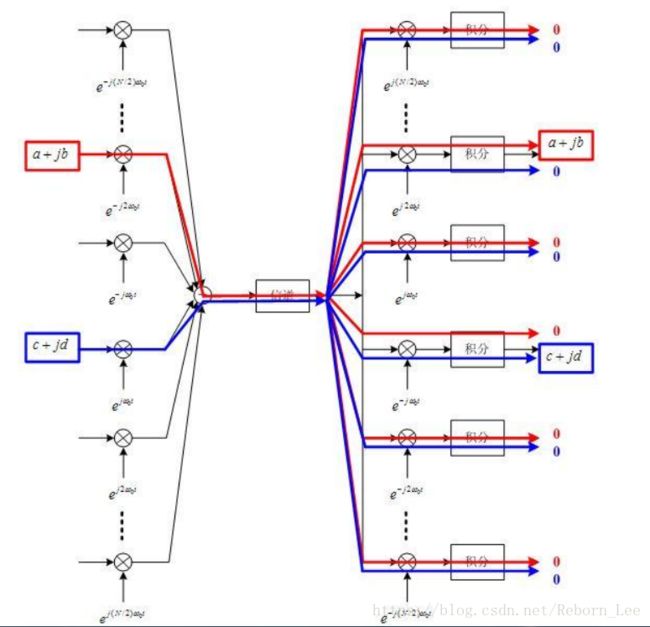
OFDM调制解调的原理大致就是如此(来自于深入浅出通信原理):
积分区间取最低频率子载波的一个周期,也就是基波的一个周期:
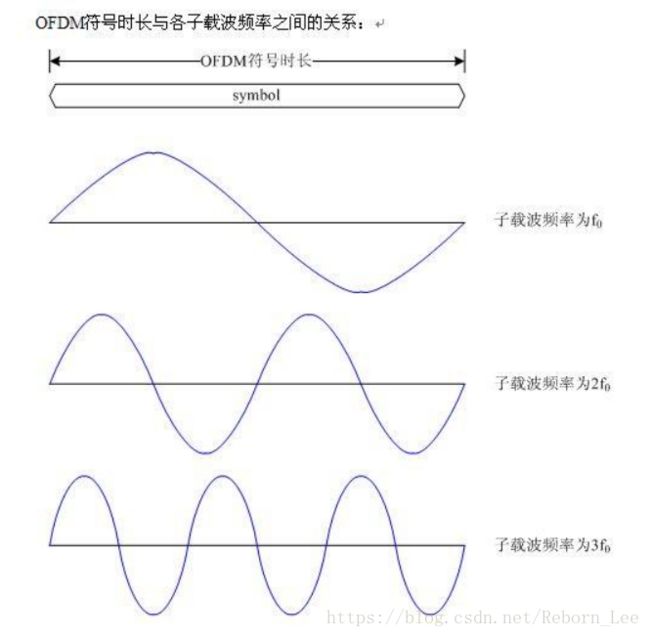
从下图可以看出OFDM符号时长与子载波频率之间的关系,其实这我们早就知道,也就是OFDM符号时长的倒数也就等于子载波间的频率间隔。
上面讲了这么多,其实都是铺垫性的内容,就说了OFDM符号时长与子载波间频率间隔之间的关系。
其实最重要的就是说子载波间之间的正交性,而这种正交性从哪里体现呢?当然是在一个OFDM符号时长内的积分为0,也可以说两个不同的子载波间的內积为0,这也是连续信号正交的定义,当然这里的內积也是连续函数之间的內积了。
下面我们要来正经的重点内容了。
第二个问题:
为什么会有子载波间的干扰呢?
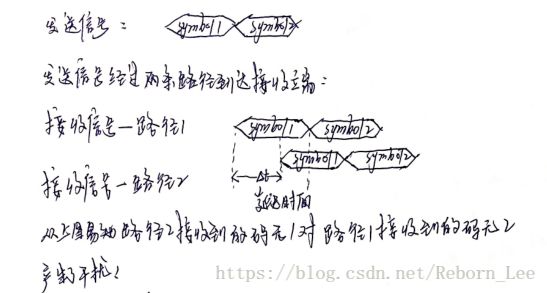
这里的干扰指的是什么呢?我们知道符号间干扰指的是第二径的第一个符号对第一径的第二个符号产生了干扰,影响人家本身的纯净。
就是这个图的意思。
好,就不买关子了,要不然会被说一个简单的内容,让你说的多么了不起似的。
子载波间的干扰就是子载波间的正交性被破坏了。
我来解释这句话,也即为什么子载波间的正交性被破坏了?
见下图:
在要发送的符号间加入了保护间隔避免了多径效应引起的符号间干扰,且这里假设多经时延等于保护间隔的长度。
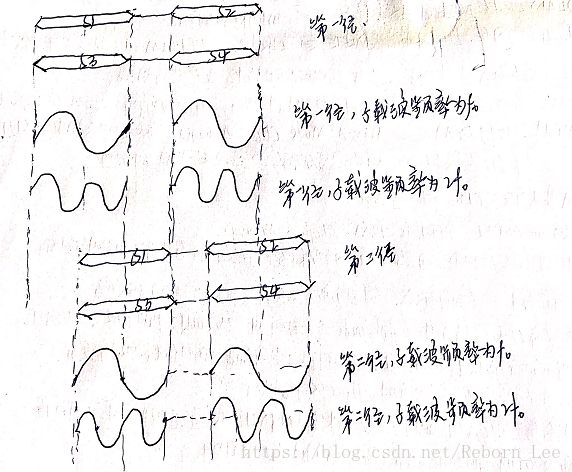
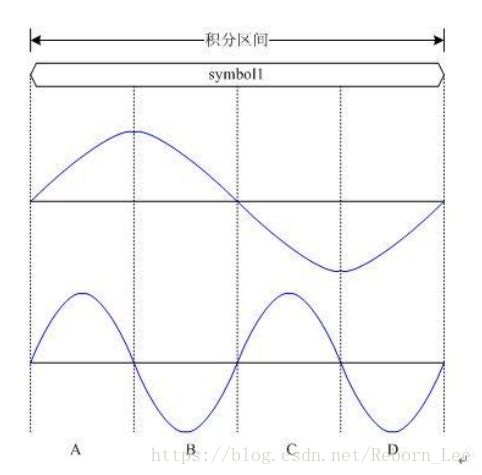
我们知道,符号是要调制子载波后得到已调信号,之后再发送出去的,(这里同样省略了射频调制的过程),本身符号s1与符号s3对应的调制子载波是相互正交的,见下图:
二者子载波间相乘在积分为0;
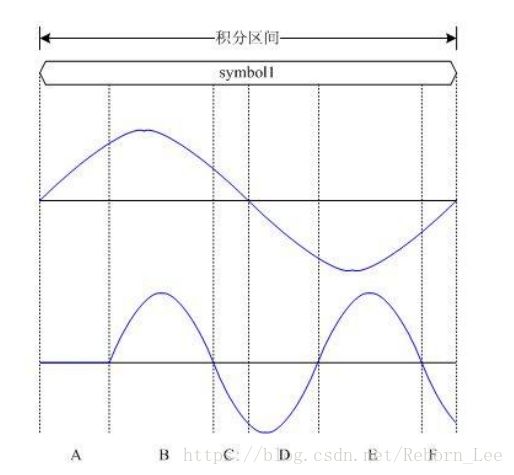
但符号s1调制频率为f0的子载波后经过第一径发送出去,符号s3调制频率为2f0的子载波后经过第二径发送出去,二者的子载波间的关系如下:
易知,二者相乘后积分不在为零,这就是说二者之间不满足正交性了。
这就是为了解决多径效应引起的码间干扰而添加保护间隔后破坏了子载波间的正交性,也就是引起了子载波间的干扰。
既然出现了子载波间的干扰问题,那么解决办法是什么呢?
下面就分析这个问题:
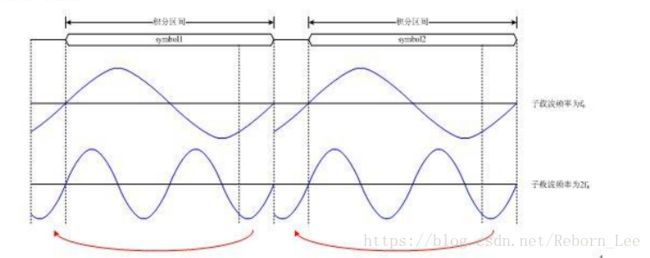
这个问题的答案显而易见,几乎每一本通信原理的书都会说,添加循环前缀。如下图:
将每个符号对应的载波后面部分(长度为保护间隔的长度)添加到该载波前面保护间隔的位置,当然原来位置处的载波还保留着。
这样每个子载波在保护间隔处就变成连续的了,也就是说在保护间隔+符号时长这段时间内子载波都是连续的了。
话虽如此,但从上图你能看出来添加循环前缀就解决了子载波间干扰了吗?
如何说明这个问题?
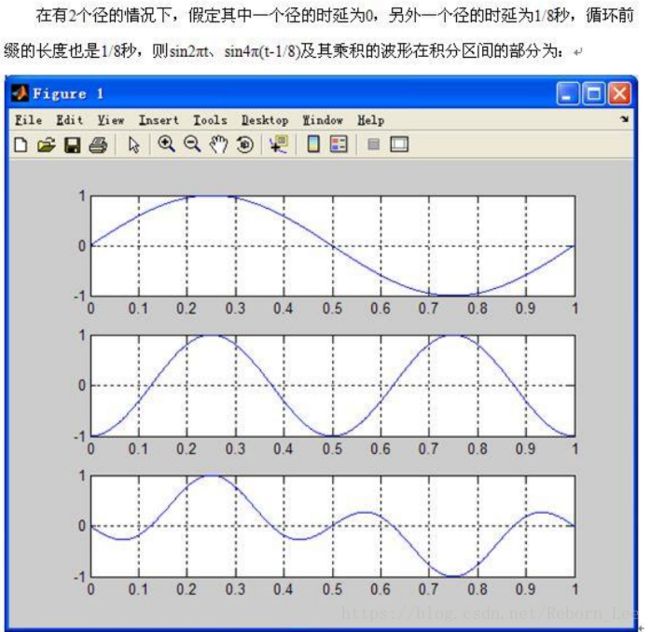
见第三个图,在积分区间内积分确实为0,这说明了加循环前缀后,二者正交;
这还没有结束,试想如果不只有两个径呢?
如果有多个径,以三个径为例,三个径肯定有两个径有时延,那么循环的长度应该为多少呢?如果循环前缀的长度以最大径延时为准,那么还会正交吗?
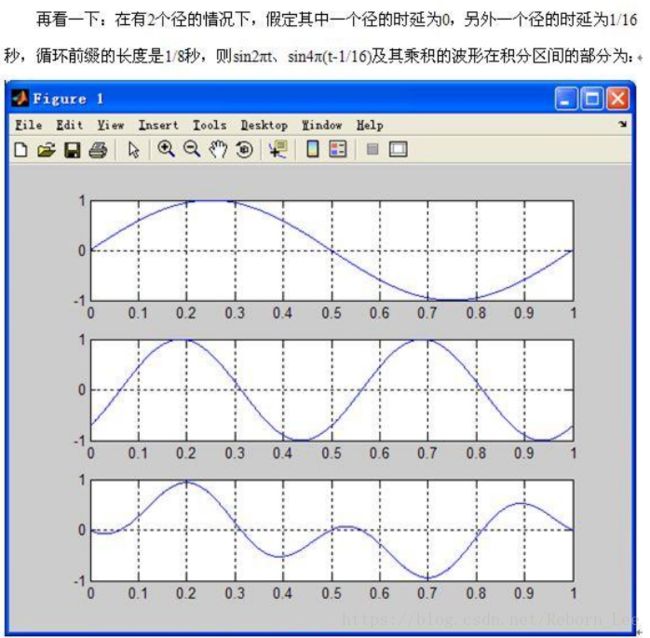
见下图:
这幅图依然是两个径的情况,但你会发现循环前缀的长度大于信号的延时,而此时这两个子载波依然正交。
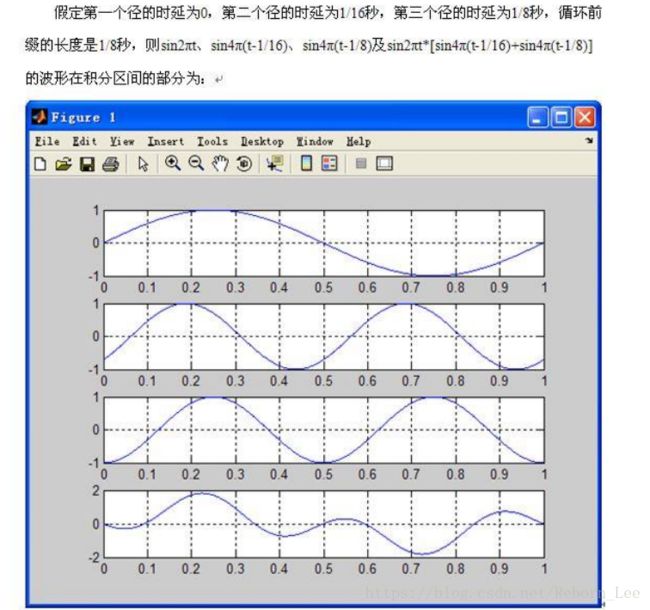
下面这幅图是三个径的情况,有了上面的两种情况,这种情况就好理解了:
频率为f0的子载波依然和频谱为2f0的子载波正交,而不管有多少个径。这就解决了子载波间干扰的问题?
其实这里的问题,还没有结束,我只是没有动力总结了。
留个问题以供思考吧!
虽然每个子载波前都添加了循环前缀,这解决了不同频率的子载波之间的正交性问题,但是频率相同的子载波,来自于不同的径之间相乘再积分还能恢复出原来的信号吗?
最后感谢《深入浅出通信原理》,这本书以及这个系列的文章真是称得上是深入浅出,它给我提供了不少想法和解决了不少疑惑。
下篇博文还是继续讲一下没有讲完的问题吧。不想留下遗憾!尽管花了不少时间。