线索二叉树(详解)
线索二叉树原理
遍历二叉树的其实就是以一定规则将二叉树中的结点排列成一个线性序列,得到二叉树中结点的先序序列、中序序列或后序序列。这些线性序列中的每一个元素都有且仅有一个前驱结点和后继结点。
但是当我们希望得到二叉树中某一个结点的前驱或者后继结点时,普通的二叉树是无法直接得到的,只能通过遍历一次二叉树得到。每当涉及到求解前驱或者后继就需要将二叉树遍历一次,非常不方便。
于是是否能够改变原有的结构,将结点的前驱和后继的信息存储进来。
二叉树结构
观察二叉树的结构,我们发现指针域并没有充分的利用,有很多“NULL”,也就是存在很多空指针。
对于一个有n个结点的二叉链表,每个节点都有指向左右孩子的两个指针域,一共有2n个指针域。而n个结点的二叉树又有n-1条分支线数(除了头结点,每一条分支都指向一个结点),也就是存在2n-(n-1)=n+1个空指针域。这些指针域只是白白的浪费空间。因此, 可以用空链域来存放结点的前驱和后继。线索二叉树就是利用n+1个空链域来存放结点的前驱和后继结点的信息。
线索二叉树
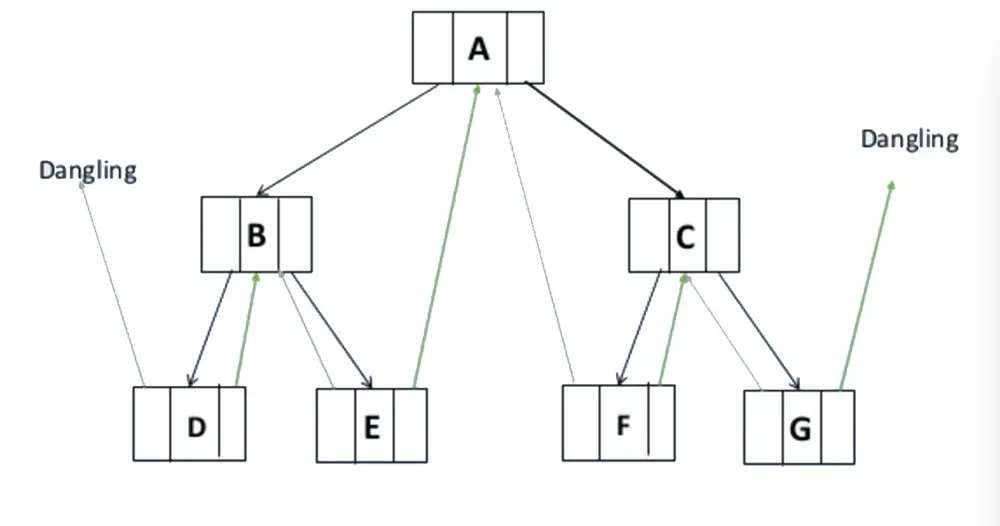
如图以中序二叉树为例,我们可以把这颗二叉树中所有空指针域的lchild,改为指向当前结点的前驱(灰色箭头),把空指针域中的rchild,改为指向结点的后继(绿色箭头)。我们把指向前驱和后继的指针叫做线索 ,加上线索的二叉树就称之为线索二叉树。
线索二叉树结点结构
如果只是在原二叉树的基础上利用空结点,那么就存在着这么一个问题:我们如何知道某一结点的lchild是指向他的左孩子还是指向前驱结点?rchild是指向右孩子还是后继结点?显然我们要对他的指向增设标志来加以区分。
因此,我们在每一个结点都增设两个标志域LTag和RTag,它们只存放0或1的布尔型变量,占用的空间很小。于是结点的结构如图所示。
结点结构
其中:
LTag为0是指向该结点的左孩子,为1时指向该结点的前驱
RTag为0是指向该结点的右孩子,为1时指向该结点的后继
因此实际的二叉链表图为
实际的二叉链表图
线索二叉树的结构实现
二叉树的线索存储结构定义如下:
typedef char TElemType;
typedef enum { Link, Thread } PointerTag; //Link==0,表示指向左右孩子指针
//Thread==1,表示指向前驱或后继的线索
//二叉树线索结点存储结构
typedef struct BiThrNode {
TElemType data; //结点数据
struct BiThrNode *lchild, *rchild; //左右孩子指针
PointerTag LTag;
PointerTag RTag; //左右标志
}BiThrNode, *BiThrTree;
二叉树线索化
线索化
对普通二叉树以某种次序遍历使其成为线索二叉树的过程就叫做线索化。因为前驱和后继结点只有在二叉树的遍历过程中才能得到,所以线索化的具体过程就是在二叉树的遍历中修改空指针。
线索化具体实现
以中序二叉树的线索化为例,线索化的具体实现就是将中序二叉树的遍历进行修改,把原本打印函数的代码改为指针修改的代码就可以了。
我们设置一个pre指针,永远指向遍历当前结点的前一个结点。若遍历的当前结点左指针域为空,也就是无左孩子,则把左孩子的指针指向pre(相对当前结点的前驱结点)。
右孩子同样的,当pre的右孩子为空,则把pre右孩子的指针指向当前结点(相对pre结点为后继结点)。
最后把当前结点赋给pre,完成后续的递归遍历线索化。
中序遍历线索化的递归函数代码如下:
void InThreading(BiThrTree B,BiThrTree *pre) {
if(!B) return;
InThreading(B->lchild,pre);
//--------------------中间为修改空指针代码---------------------
if(!B->lchild){ //没有左孩子
B->LTag = Thread; //修改标志域为前驱线索
B->lchild = *pre; //左孩子指向前驱结点
}
if(!(*pre)->rchild){ //没有右孩子
(*pre)->RTag = Thread; //修改标志域为后继线索
(*pre)->rchild = B; //前驱右孩子指向当前结点
}
*pre = B; //保持pre指向p的前驱
//---------------------------------------------------------
InThreading(B->rchild,pre);
}
增设头结点
线索化后的二叉树,就如同操作一个双向链表。于是我们想到为二叉树增设一个头结点,这样就和双向链表一样,即能够从第一个结点正向开始遍历,也可以从最后一个结点逆向遍历。
增设头结点
如上图,在线索二叉链表上添加一个head结点,并令其lchild域的指针指向二叉树的根结点(A),其rchild域的指针指向中序遍历访问的最后一个结点(G)。同样地,二叉树中序序列的第一个结点中,lchild域指针指向头结点,中序序列的最后一个结点rchild域指针也指向头结点。
于是从头结点开始,我们既可以从第一个结点顺后继结点遍历,也可以从最后一个结点起顺前驱遍历。就和双链表一样。
双链表
增设头结点并线索化的代码实现
//为线索二叉树添加头结点,使之可以双向操作
Status InOrderThreading(BiThrTree *Thrt,BiThrTree T){
if(!(*Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) exit(OVERFLOW); //开辟结点
(*Thrt)->LTag = Link;
(*Thrt)->RTag = Thread; //设置标志域
(*Thrt)->rchild = (*Thrt); //右结点指向本身
if(!T) {
(*Thrt)->lchild = (*Thrt);
return OK; //若根结点不存在,则该二叉树为空,让该头结点指向自身.
}
BiThrTree pre; //设置前驱结点
//令头结点的左指针指向根结点
pre = (*Thrt);
(*Thrt)->lchild = T;
//开始递归输入线索化
InThreading(T,&pre);
//此时结束了最后一个结点的线索化了,下面的代码把头结点的后继指向了最后一个结点.
//并把最后一个结点的后继也指向头结点,此时树成为了一个类似双向链表的循环.
pre->rchild = *Thrt;
pre->RTag = Thread;
(*Thrt)->rchild = pre;
return OK;
}
遍历线索二叉树
线索二叉树的遍历就可以通过之前建立好的线索,沿着后继线索依依访问下去就行。
//非递归遍历线索二叉树
Status InOrderTraverse(BiThrTree T) {
BiThrNode *p = T->lchild;
while(p!=T){
while(p->LTag==Link) p = p->lchild; //走向左子树的尽头
printf("%c",p->data );
while(p->RTag==Thread && p->rchild!=T) { //访问该结点的后续结点
p = p->rchild;
printf("%c",p->data );
}
p = p->rchild;
}
return OK;
}
完整代码
#include
#include
//函数状态结果代码
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
//Status是函数的类型,其值是函数结果状态代码
typedef int Status;
typedef char TElemType;
typedef enum { Link, Thread } PointerTag;
typedef struct BiThrNode {
TElemType data;
struct BiThrNode *lchild, *rchild;
PointerTag LTag;
PointerTag RTag;
}BiThrNode, *BiThrTree;
//线索二叉树初始化
Status CreateBiThrNode(BiThrTree * B) {
char ch;
scanf("%c", &ch);
if(ch=='#') *B = NULL;
else{
if(!((*B) = (BiThrNode *)malloc(sizeof(BiThrNode)))) exit(OVERFLOW);
(*B)->data = ch;
(*B)->LTag = Link;
(*B)->RTag = Link;
CreateBiThrNode(&(*B)->lchild);
CreateBiThrNode(&(*B)->rchild);
}
return OK;
}
//线索二叉树线索化
void InThreading(BiThrTree B,BiThrTree *pre) {
if(!B) return;
InThreading(B->lchild,pre);
if(!B->lchild){
B->LTag = Thread;
B->lchild = *pre;
}
if(!(*pre)->rchild){
(*pre)->RTag = Thread;
(*pre)->rchild = B;
}
*pre = B;
InThreading(B->rchild,pre);
}
//为线索二叉树添加头结点,使之可以双向操作
Status InOrderThreading(BiThrTree *Thrt,BiThrTree T){
if(!(*Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) exit(OVERFLOW);
(*Thrt)->LTag = Link;
(*Thrt)->RTag = Thread;
(*Thrt)->rchild = (*Thrt);
if(!T) {
(*Thrt)->lchild = (*Thrt);
return OK; //若根结点不存在,则该二叉树为空,让该头结点指向自身.
}
BiThrTree pre;
//令头结点的左指针指向根结点
pre = (*Thrt);
(*Thrt)->lchild = T;
//开始递归输入线索化
InThreading(T,&pre);
//此时结束了最后一个结点的线索化了,下面的代码把头结点的后继指向了最后一个结点.
//并把最后一个结点的后继也指向头结点,此时树成为了一个类似双向链表的循环.
pre->rchild = *Thrt;
pre->RTag = Thread;
(*Thrt)->rchild = pre;
return OK;
}
//非递归遍历线索二叉树
Status InOrderTraverse(BiThrTree T) {
BiThrNode *p = T->lchild;
while(p!=T){
while(p->LTag==Link) p = p->lchild; //走向左子树的尽头
printf("%c",p->data );
while(p->RTag==Thread && p->rchild!=T) { //访问该结点的后续结点
p = p->rchild;
printf("%c",p->data );
}
p = p->rchild;
}
return OK;
}
int main() {
BiThrTree B,T;
CreateBiThrNode(&B);
InOrderThreading(&T,B);
printf("中序遍历二叉树的结果为:");
InOrderTraverse(T);
printf("\n");
}
//测试数据:abc##de#g##f###