BSGS算法 可以快速的求出，满足a^x ≡ b(mod p)的最小的非负整数x （p必须为质数，即 gcd(a,p) == 1）
我们先将x拆分成i*m-j的形式（其中m为sqrt(p)向上取整的值，则原式化为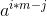 
≡ b (mod p) ) 显然 0<=j
移向后得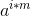 
≡ b*
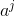(mod p)
我们从 0-m 枚举 j，并将 b*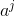 的所有值存入map中
接着在从 1-m 枚举 i，算出所有的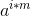
如果一个 i 对应的 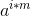的值已经在 map 中，则表明 i*m-j 为一个解，输出此时的解即可
因为 j<=m，所以求出的解随 i 的增大而减小，所以最先求出的 i 所对的解，即为所求的解
根据 poj2417所写 http://poj.org/problem?id=2417
//#include
#include
#include
#include
#include
另外，使用map可能会造成时间超限，所以有时需要自己手写hash表，但这会用掉大量内存（依然是 poj2417）
//#include
#include
#include
#include
#include
但是上面的哈希表不知道为什么，在https://ac.nowcoder.com/acm/contest/885/C中会段错误，而且这道题分块很有讲究，所以有更好的板子如下：
#define ll long long
const int MOD=1e7;
ll quickpow(ll a,ll b,ll mod){
ll ans=1;
while(b){
if(b&1)
ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
ll hs[MOD], head[MOD], Next[MOD], id[MOD], top;
void insert(ll x, ll y){
ll k = x % MOD;
hs[top] = x;
id[top] = y;
Next[top] = head[k];
head[k] = top++;
}
ll find(ll x){
ll k = x % MOD;
for (ll i = head[k]; i != -1; i = Next[i])
if (hs[i] == x)
return id[i];
return -1;
}
ll up,down,mul;
//unordered_mapM;
void init(){
memset(head,-1,sizeof(head));
top=0;
}
void initBSGS(ll y,ll p){
//M.clear();
init();
up=ceil(pow(p,2.0/3));//在一般情况下，大步小步的值均为 sqrt(p)，但该题会有q次询问，每次询问都要在哈希表中进行查找，所以我们要让小步的值尽可能的小
down=ceil(pow(p,1.0/3));
ll num=1;
for(int i=0; i<=up; i++){
if(i==up)
mul=num;
insert(num,i);
//M[num]=i;
num=num*y%p;
}
}
ll BSGS(ll y,ll z,ll p){
ll num=quickpow(z,p-2,p);
for(int i=1; i<=down+1; i++){
num=num*mul%p;
ll f=find(num);
if(f!=-1) return i*up-f;
//if(M.count(num)) return i*up-M[num];
}
return -1;
}
扩展BSGS是在模数不为质数时用的
直接上代码，转自 https://www.cnblogs.com/TheRoadToTheGold/p/8478697.html
#include
