Java 排序之选择排序、堆排序
本文首发于我的个人博客:https://staunchkai.com
接上一篇文章:Java 排序之插入排序、希尔排序
三、选择排序
1. 算法简介
选择排序相对于上一篇文章记录的插入排序、希尔排序要简单一些,它比较直观。它的基本思路为:把第一个元素依次和后面的所有元素进行比较,第一次结束后,就会有最小值出现在最前面,依次类推。
2. 算法分析
假设有一个数组:
int[] arr = { 54, 40, 60, 55, 52 };
- 用第零个元素
54先和40相比,40小,54放到原来40的位置,用40继续和其他的比,没有比它小的了,第一轮结束,这时的顺序为:
{ 40, 54, 60, 55, 52 };
- 用第一个元素
54和后面的进行比较,过程同上,有比它小的就把小的拿出来,把它放进去,用小的继续比 - 依次类推…
3. 算法图解附视频
视频 点此查看。
4. 算法代码
import java.util.Arrays;
public class SelectionSort {
public static void main(String[] args) {
int[] arr = { 54, 40, 60, 55, 52 };
sort(arr);
System.out.println(Arrays.toString(arr));
}
public static void sort(int[] arr) {
for (int x = 0; x < arr.length - 1; x++) {
for (int y = x + 1; y < arr.length; y++) {
if (arr[y] < arr[x]) {
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
}
}
}
}
四、堆排序
1. 算法简介
堆排序(Heapsort)是经典的排序算法之一,在面试的时候比较常见,堆排其实是一个看起来复杂其实并不复杂的排序算法。利用堆积树(堆)这种数据结构所设计的一种排序算法,它也是一种选择排序算法。可以利用数组的特点快速定位指定索引的元素,堆分为大根堆和小根堆,近似 完全二叉树。
2. 算法分析
先一步步了解其中的各个方面。
1) 什么是堆?
在此处提到的堆一般都是指 二叉堆,它满足两个特性:
- 父节点的键值大于或等于(小于或等于)任何一个子节点的键值
- 每个节点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)
2) 什么是堆调整?
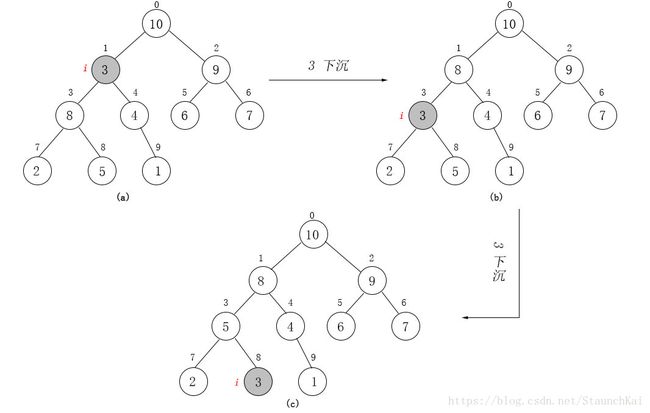
这是为了保持堆的特性而作出的一个操作,对某一个节点为根的子树做堆调整,就是将根节点进行 下沉 操作(通过交换完成),一直下沉到合适的位置,使得子树满足堆的性质。
例如:(最大堆的调整)
- 在对应的数组元素
A[i],左边子节点A[Left(i)]和右边子节点A[Right(i)]中找到最大的一个,将其下标存储在 largest 中; - 如果
A[i]已经是最大的元素,则程序结束; - 否则,
i的某个子节点为最大的元素,将A[largest]与A[i]交换; - 再从交换的子节点开始,重复上面的步骤。
一般做一次堆调整的时间复杂度为:log(n)
下图为对元素 3 为根节点的子树做一次堆调整的示意图:
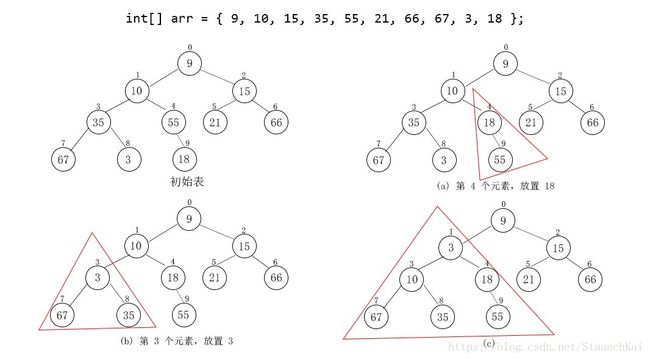
3) 如何建堆?
建堆是通过不断地堆调整,使得整个二叉树中的数满足堆的特性。在数组中,一般从下标为 n/2 的数开始做调整,一直到下标为 0 的数(因为下标大于 n/2 的数都是叶子节点,其子树已经满足堆的特性)。下图为一个示例:
3) 如何进行堆排序?
堆排序是在上述 3 中对数组建堆的操作之后完成的。
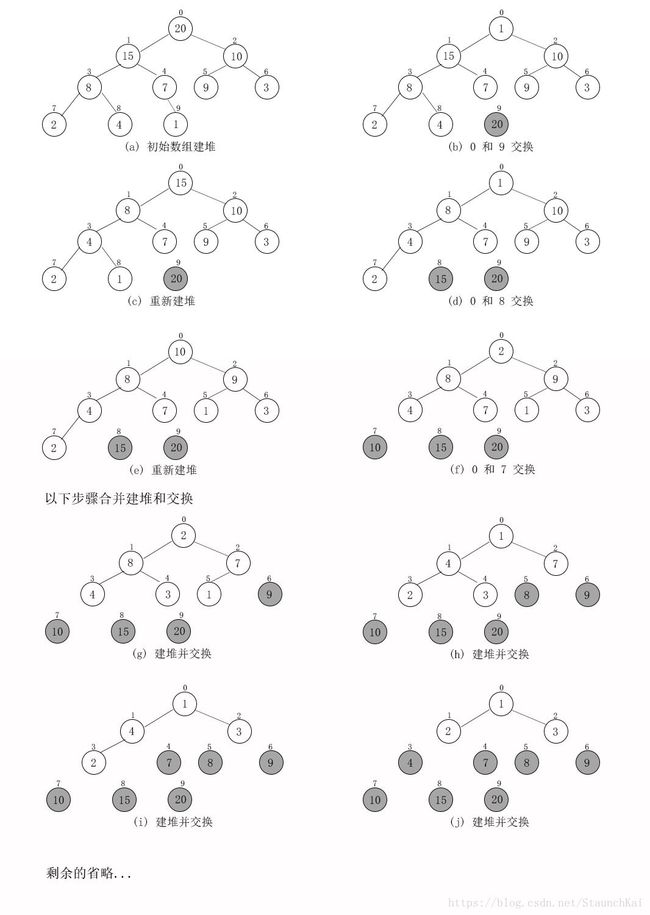
数组存储成堆得形式后,第一次将 A[0](即堆顶) 与最后一个记录 A[n-1] 交换,由此得到一个新的无序区 A[0...n-2] 和一个有序区 A[n-1]。再对 A[0...n-2] 重新恢复堆,第二次将 A[0] 与 A[n-2] 交换,再对 A[0...n-3] 重新恢复堆,重复这样得操作,直到 A[0] 与 A[1] 交换。由于每次都是将最小的数据并入到后面的有序区间,故操作完成后整个数组就有序了。
如下图所示:
3. 算法代码
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int[] data = { 11, 22, 10, 55, 44 };
sort(data);
System.out.println(Arrays.toString(data));
}
public static void sort(int[] data) {
MaxHeap h = new MaxHeap();
h.init(data);
for (int i = 0; i < data.length; i++)
h.remove();
System.arraycopy(h.queue, 1, data, 0, data.length);
}
private static class MaxHeap {
void init(int[] data) {
this.queue = new int[data.length + 1];
for (int i = 0; i < data.length; i++) {
queue[++size] = data[i];
fixUp(size);
}
}
private int size = 0;
private int[] queue;
public void remove() {
swap(queue, 1, size--);
fixDown(1);
}
// fixdown
private void fixDown(int k) {
int j;
while ((j = k << 1) <= size) {
if (j < size && queue[j] < queue[j + 1])
j++;
if (queue[k] > queue[j]) // 不用交换
break;
swap(queue, j, k);
k = j;
}
}
private void fixUp(int k) {
while (k > 1) {
int j = k >> 1;
if (queue[j] > queue[k])
break;
swap(queue, j, k);
k = j;
}
}
}
/*
* 交换数组中的两个元素
*/
public static void swap(int[] data, int i, int j) {
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}