搜索算法Search开篇
最近在学高级人工智能这门课,老师第二节课就讲的很硬核啊,老师讲解了一系列的搜索算法,现在做一下笔记和总结部分。(搜索这一讲是自动化所吴老师讲的,很厉害)
我们一般讲搜索都是讲路径规划问题,就是怎么从初始位置到目的地最近呢?我们怎么进行合理的规划。基于此我们将搜索问题总结为下面三种问题:
- 无信息搜索 Uninformed Search
- 启发式搜索Informed Search
- 局部搜索 Local Search
一:概念
无信息搜索也被称为盲目搜索,意味着该搜索策略没有超出问题定义提供的状态之外的附加信息。所有能做的就是生成后继节点。
启发式搜索(Heuristically Search)又称为有信息搜索(Informed Search),它是利用问题拥有的启发信息来引导搜索,达到减少搜索范围、降低问题复杂度的目的,
局部搜索:考虑局部最优解
我们看一下一个搜索问题是有几部分构成的呢?
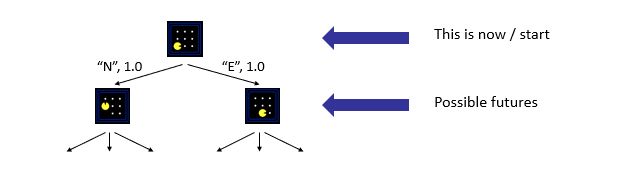
比如我们以前玩过的“外星人吃豆豆”的小游戏,一个外星人怎么样才可以将屏幕上的所有的豆子吃干净呢?按照地图来讲,这个外星人可以东西南北(EWSN)转向,并且可以朝着任意一个方向走一步,走这个一步的过程中,有可能会吃掉豆子,有可能该地方的豆子已经吃过了,为空。那么我们称外星人在每次移动一次的为一个状态,所有的状态组成了状态空间(State Space),外星人在每一次状态之后会进行抉择下一步应该怎么走,我们称为后继函数(Successor Function),当然了移动的过程中既包含了动作(Actions),也包含了代价(Costs)。我们初始位置所在的状态称之为初始状态,最后一个豆子被吃干净的状态成为目标状态,我们检验外星人是否成功,就拿外星人移动的最终状态和目标状态进行对比,如果一致,你可以说外星人成功了!这个对比的过程成为目标测试。而外星人从初始状态到最终状态的整个移动过程,我们称为该搜索问题的一个解。可以看到这个解就是一个行动队列,经过这个行动队列之后,外星人将初始状态转换成了目标状态。
经过上面的外星人吃豆子的举例,我们可以知道搜索问题其实就是对原问题的一个建模过程,这个模型就是解决外星人从初始状态转换成了目标状态的一个个方案。
总结如下:
搜索问题的构成(组成部分):
- 状态空间(环境中的每一个细节,状态的集合)
- 后继函数(行动Actions+代价Costs)-->下一个状态(把行动形式化成为一个后继函数)
- 初始状态(我最开始在什么地方)
- 目标测试(当前状态是不是达到了我们的目标)
- 求解:一个行动序列
我们举一个例子可以让我们更好的了解,搜索问题每个部分:
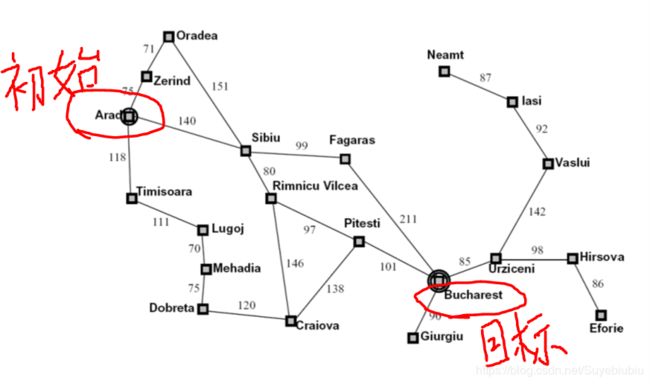
例子:罗马尼亚的旅行
我们想要从Arad到达Bucharest,姑且认为是A和B两个位置,在这个旅行过程中,我们可以总结该搜索问题的构成部分有:
状态空间:有所有城市和这个旅行的人构成
后继函数:规划去相邻的下一个城市,代价就是路程(只关心下一步怎么走)
初始状态:在A那个位置
目标测试:看最终状态是不是等于B,IsState==Bucharest
解:就是你从A到B这一过程中的行动序列
1.1 状态数量问题分析
我们怎么判断一个问题的状态数量呢?分析状态数量所在的量级有助于我们分析选择所采纳的算法。
比如上面的这个外星人吃豆子这个世界中,我们看到这个世界是有5*6个点组成的,我们来分析一下这个世界描述中的状态,豆子位置状态是120种(因为5*6*4=120,这里豆子也是有方向的,4个方向),我们还可以看到食物豆子一共有30个,我们再分析一下怪兽状态,2个怪兽只能在最右侧那6个位置移动,因此怪兽的状态是2*6=12个,外星人状态朝向有四个方向NSEW。
综上我们看一下数量:
- 世界状态一共有多少个数量呢?
120*(2^30)*(12^2)*4 120指的是豆子世界的状态,豆子一共有30个,有两种情况,被吃掉了或者没有被吃掉,所以是2^30,两个小怪兽的状态12个,因为小怪兽可以有2个朝向问题,因此最终的状态数量是12^2,最后的4个指的是外星人有4个方向的朝向。
- 路径规划状态有多少个呢?
120个,状态只描述豆子的位置,相对世界状态已经下降了很多个量级
- “吃光豆子”状态数量?
120*(2^30) 这个数量只与豆子的位置状态和豆子的数量状态有关
1.2 状态空间的表示
我们经过上面的讲解相信大家对状态空间有了一定的认识,那么这么复杂的状态空间我们应该怎么去表示它呢?我们引入两种表示方法,状态空间图和搜索树。
1.2.1 状态空间图
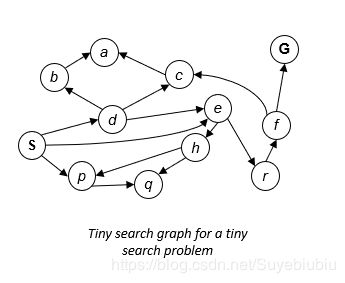
状态空间图是指用图的形式表示状态空间,搜索问题的更进一步的数学表达。图中的每一个节点都对应了一个状态,状态之间的连接边就表示相对应的行动,这个边也是有方向的。目标检测就是判断当前的状态是不是在目标集合中(这个集合有可能有一个,也有可能有多个)。在状态空间图中,每个状态只会出现一次,每个状态通过行动(后继函数)进行连接。因为有时候问题规模比较大,我们几乎不在内存中构建完整的状态空间图,但是它是非常有用的。
1.2.2 搜索树
同样树形结构也是一种特殊的图结构,在搜索树中有一下几个特点:
- 根节点对应了初始状态
- 子节点对应了父节点的后继
- 节点显示状态,但对应的是到达这些状态的行动
- 对于大多数问题,实际上并不构建整棵树
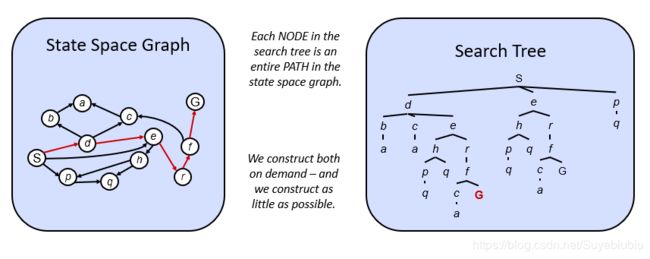
1.2.3 状态空间图 VS 搜索树
- 1.在搜索树中每一个节点是一个完整的路径(表示一个序列的行动)
- 2.在实际应用中,并不是把整个搜索树建立,而是根据需要,构建需要的树就够了
我们再看上图整个例子,左面有四个节点,我们要是将左侧状态空间图转化为搜索树的话,那么整个搜索树将是无穷大小的。因为这个图中有环,环的结构在搜索树中导致无穷。
二:树搜索
我们接下来探讨怎么在我们定义好的搜索树中进行我们的搜索问题,还是上面那个旅行问题。
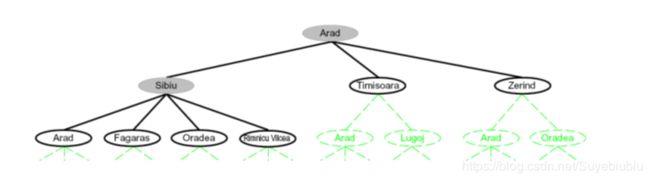
我们首先构建一棵树,Arad是初始位置,作为根节点。
我们再构建这棵树的过程中要思考以下几个问题:
- 扩展出潜在的行动 (tree nodes)
- 维护所考虑行动的边缘(fringe)节点
- 试图扩展尽可能少的树节点
通常情况下,我们研究一个搜索算法特性的时候,要考虑以下因素:
- 完备性:当问题有解时候,要保证能找到一个解
- 最优性:保证能找到最优解(最小损耗路径)
- 时间复杂度
- 空间复杂度
2.1 深度优先搜索(DFS)(Depth-First Search)
2.2 广度优先搜索(BFS)(Breadth-First Search)
2.3 深度优先搜索(DFS) VS 广度优先搜索(BFS)
2.4 迭代深入搜索(Iterative Deepening)
2.5 代价敏感搜索(Cost-Sensitive Search)
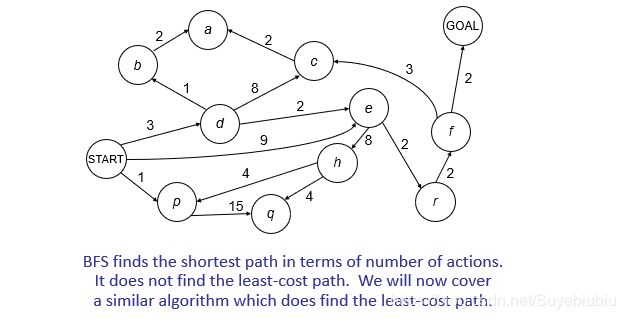
按照我的理解,就是BFS等算法找到最短路径。但是有一个问题就是最短路径并不一定是代价最低的路径,因此我们想出来一个类似的算法,它能找到成本最低的路径。算法开始关注了路程中的代价问题,两个节点之间的代价不再等效处理。更加符合应用规则。
2.6 代价一致搜索(Uniform Cost Search)
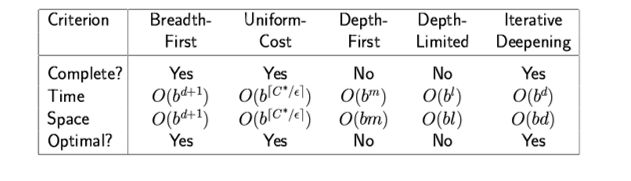
附录:我会在其余的博客中分别对其展开。这里先放下各种搜索算法的对比数据:
好了,经过上面的啰嗦,上面所罗列的搜索算法都是无信息搜索,我们接下来会讲启发式搜索和局部搜索。
欠着大家这6个搜索算法的具体介绍。。。。。。