二分类和多分类问题下的评价指标详析(Precision, Recall, F1,Micro,Macro)
多分类问题下的评价指标分析(Precision, Recall, F1)
- 二分类下的评价指标
- Accuracy
- 几个常用的术语
- Precision
- Recall
- F1-score
- 多分类问题下的评价指标
- 多分类问题下的micro-F1(微平均)和macro-F1(宏平均)
- micro微平均
- macro-宏平均
二分类下的评价指标
Accuracy
分类算法有很多,不同分类算法有很多不同的变种。不同的分类算法有着不同的原理和结构,同时在不同的数据集上变现的效果也不同,我们需要根据特定的任务进行算法的选择,如何选择分类,如何评价一个分类算法的好坏,就需要一定能量化的评价指标进行评价。这里最比较常见和易于理解的就是Accuracy,它的公式也比较简单:划分正确的样本数 / 所有的样本数。代表的即是模型对所有样本的分类准确率。
但是为什么有了Accuracy还不够呢?因为Accuracy这一指标在Unbalanced数据集上的表现很差。举个例子就是,假设我们的数据集中,有990个负样本,而只有10个正样本,则我们的模型可以将这1000个样本结果都预测为负样本,此时模型的分类准确路Accuracy仍然可以有99%,而此时该模型其实并没有学习到数据中的特征分布。比如利用该模型去预测是否会发生地震,则会完全失去预警功能。
所以我们就要引入了其他几种评价指标。刚刚提到过,上述模型无法对正样本进行有效的预测,即使准确率高达99%。那么为了去衡量其在正样本中的分类能力,就有了Precision和Recall两个指标,Precision和Recall都是着重关注模型在正样本中的分类能力。
在介绍接下来的内容前,首先我们先假设模型的预测结果为pred=[0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1],标签为Label=[1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1]
几个常用的术语
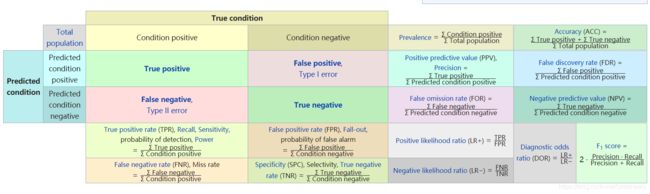
这里首先介绍几个常见的模型评价术语,现在假设我们的分类目标只有两类,计为正例(positive)和负例(negative)分别是:
1)True positive(TP): 被正确地划分为正例的个数,即实际为正例且被分类器划分为正例的样本数
2)False positive(FP):被错误地划分为正例的个数,即实际为负例但被分类器划分为正例的样本数。
3)False negative(FN):被错误地划分为负例的个数,即实际为正例但被分类器划分为负例的样本数
4)True negative(TN):被正确地划分为负例的个数,即实际为负例且被分类器划分为负例的样本数
如何理解True/False positive/negative呢?
就是第一个True/False表示的时候分类器的结果是否正确,而positive/negative表示的是分类器的结果。所以FP表示的是分类器的分类结果为positive,False表示分类器的分类结果并不正确,即实际应该为negative。所以FP表示的就是实际为负例但被分类器划分为正例的样本数。
Precision
精确率表示的是在所有预测结果为真中的准确率。公式如下:
![]()
其中Tp表示的在预测结果中,预测为真同时正确的样本数,FN表示在预测结果中,预测为真但实际为假的样本数。Tp+Fp所表示的实际上就是预测结果中所有的正例数。比如在上面举例的pred和label中,pred预测结果中的正例数为7,而通过pred和label的对比可以看出,正例中预测正确的个数为6个(除了第5个位置上的0预测成了1)。所以,此时的precision=6/(6+1) = 6/7。
所以可以看出,precision关注的是模型在预测结果为真中的准确率,表示的是模型在预测结果为真时的可信度,而不关心模型能从真正的正例中识别出多少正例。比如,如果我预测结果为3个1且都预测正确,则此时的precision=1。
Recall
Recall召回率表示的是在Label中的所有正类中被预测为正类的比例。衡量的是模型对实际正类的提取能力。
![]()
其中FN表示的是实际上为真,但被分类器预测为假。因此Tp+FN表示的相当于就是Label中所有正类的个数。所以同样可以看出Recall关注的是模型在所有真正正类中的准确率,反应了一个模型能识别出正类的能力。同样以上面的例子为例,Tp仍然为6,此时FN=2(第一个位置和第八个位置)。此时Tp+FN=8,也正好等于label中的所有为正类1的个数。而当我预测结果为3个1且都正确时,此时的Recall=3/8。
因此以上两个评价指标则将模型在正类中的分类能力进行了划分。Precision衡量模型预测正类时的准确率,Recall衡量模型识别出正类的能力。
F1-score
表示的是精确率和召回率的调和平均。由上面的分析可知,Precision和Recall反应了模型两个不同方面的能力,而F1-score相当于是表示模型在这两方面的一个综合水平。
![]()
从实际应用来理解Precision和Recall的区别可以是,比如宁可错杀一千,不可放过一个,体现的就是召回率的思想,即是要求识别“罪犯”的能力很强。而在一些需要精准性比较高的领域,则要求每次的预测结果都要十分精准,就需要比较高的Precision。同时也可以发现,Precision和Recall两者往往不能兼得。比如同样的宁可错杀一千,不可放过一个,就意味着要牺牲精确性。因为此时在你识别出的“罪犯”中真正的“罪犯”占的是少数,所以精确性就会降低。所以需要在具体的实际应用中,选择是更看重精确性还是召回率,或者利用F1-score找到两者比较平衡的一个点。
多分类问题下的评价指标
在二分类问题中,只有0,1两种分类情况。而实际中我们经常会遇到多分类问题,比如NER中对每个字符判断其所属类别等等。在这种情况下,我们可以把每个类别单独视为正类,其他的类别视为负类,因此相当于对每个类别都转化成了一个“二分类的情况”。
链接:https://en.wikipedia.org/wiki/Confusion_matrix
多分类的情况可以用一个混淆矩阵来表示,例如下面的混淆矩阵。可以看出混淆矩阵是一个n*n的矩阵,n表示多分类的类别数。
M = [
[325, 32, 9, 0, 0, 2, 236],
[57, 750, 454, 20, 0, 11, 23],
[0, 128, 157, 71, 0, 11, 0],
[8, 0, 160, 112, 0, 0, 0],
[0, 321, 39, 2, 150, 0, 0],
[0, 145, 52, 30, 0, 189, 0],
[48, 35, 0, 0, 0, 0, 237]
]
其中对角线上表示的是分类正确的样本。通过上图可以看出,行代表了真实的类别,列代表了预测的类别。第一行中的[325, 32, 9, 0, 0, 2, 316],表示有325个类别1被预测为类别1,有32个类别1被预测为类别2,有9个类别1被预测为类别3,有2个类别1被预测为类别6,有236个类别1被预测为7。
所以真实的正类共有325+32+9+2+236=604,其中FN=32+9+2+236=279,TP=325。
因此可以得出此类别1下的召回率为325/604=0.538
同样的由于列代表的是预测结果,所以计算精确率的时候要关注列的结果。
第一列[325, 57, 0, 8, 0, 0, 48]表示的是在预测结果中,有325个类别1被预测为类别1, 有57个类别2预测成了类别1,有8个类别4预测成了类别1,有48个类别7预测成了类别1。所以此时仍然可以得出:
TP=325,FP=57+8+48=113 (FP表示分类器预测为正类但实际为负类的样本数)。
因此同样可以得出类别1下的Precision=325/438=0.742
以此类推可以对每一类别计算其对应的Precision和Recall。这里要理解就是为什么Precision是计算的列和,Recall计算的是行和。因为列代表的是预测结果,行代表的是真实结果。
多分类问题下的micro-F1(微平均)和macro-F1(宏平均)
在n个二分类混淆矩阵上要综合考察评价指标的时候就会用到宏平均和微平均。也就是在计算多分类问题时的F1-score的两种策略。
micro-F1(微平均):Calculate metrics globally by counting the total true positives, false negatives and false positives.
macro-F1(宏平均):Calculate metrics for each label, and find their unweighted mean. This does not take label imbalance into account.
通过上面的定义可以发现,micro的意思就是对所有类别求出总体的TP、FN、FP,然后再计算出总体的Precison、Recall最后再利用F1=2*P*R/(P+R)来计算出F1-score。而macro的意思就是先对每个类别求出对应的Precision、Recall、F1这些指标,然后进行平均来求出总体的F1-score。
看下面的例子:
y_label = [1, 1, 3, 0, 2, 2, 1, 3, 0]
y_pred = [1, 1, 2, 0, 0, 2, 3, 3, ,0]
假设有这个简单的模型输出结果,y_pred利用argmax取出每个softmax之后的最大位置的值。可以看出总共有4类。
micro微平均
对于类别0,分析时可以将其他类看作负类,则上式可以转化为:
y_pred=[0, 0, 0 ,1, 0, 0, 0, 0, 1]
y_label=[0, 0, 0, 1, 1, 0, 0, 0, 1]
可以看出此时的TP=2, FP=0,FN=1。
对于类别1,同样进行转化为:
y_pred=[1, 1, 0, 0, 0, 0, 1, 0, 0]
y_label=[1, 1, 0, 0, 0, 0, 0, 0, 0]
可以看出此时的TP=2, FP=1,FN=0
对于类别2,同样进行转化为:
y_pred=[0, 0, 1, 0, 0, 1, 0, 0, 0]
y_label=[0, 0, 0, 0, 1, 1, 0, 0, 0]
可以看出此时的TP=1,FP=1,FN=1
对于类别3,同样进行转化Wie:
y_pred=[0, 0, 0, 0, 0, 0, 1, 1, 0]
y_label=[0, 0, 1, 0, 0, 0, 0, 1, 0]
可以看出此时的TP=1,FP=1,FN=1
所以综上可以得出:
TP=2+2+1+1=6,FP=0+1+1+1=3,FN=1+0+1+1=3
所以可以得出:
micro-P=6/(6+3)=0.667
micro-P=6/(6+3)=0.667
micro-F1=2*P*R/(P+R)=0.667
macro-宏平均
按照上述的做法:
类别0时:
macro-P=2/2=1
macro-R=2/(2+1)=2/3
macro-F1=2*P*R/(P+R)=4/5
类别1时:
macro-P=2/(2+1)=2/3
macro-R=2/(2+0)=1
macro-F1=2*P*R/(P+R)=4/5
类别2时:
macro-P=1/(1+1)=1/2
macro-R=1/(1+1)=1/2
macro-F1=2*P*R/(P+R)=1/2
类别3时:
macro-P=1/(1+1)=1/2
macro-R=1/(1+1)=1/2
macro-F1=2*P*R/(P+R)=1/2
所以此时,最终的macro结果为:
macro-P=(1+2/3+1/2+1/2) / 4 = 2/3
macro-R=(2/3+1+1/2+1/2) / 4 = 2/3
macro-F1=(4/5+4/5+1/2+1/2) / 4= 13/20
以上就是在micro微平均和macro宏平均上的计算过程。便于理解两者之间的原理和差异。宏平均比微平均更合理,但也不是说微平均一无是处,具体使用哪种评测机制,还是要取决于数据集中样本分布。类别极度不均衡的时候也需要考虑用 weighted进行处理,用 Macro 一般情况会拉低(因为小数量的类别一般情况下预测不好,但最后又是 mean)。
其他资料:
详解多分类模型的Macro-F1/Precision/Recall计算过程
sklearn中 F1-micro 与 F1-macro区别和计算原理
多分类问题中的精确率与召回率