在前面的博文中,已经介绍了阵列信号处理的一些基本概念,并介绍了线阵的导向向量结构以及波束相关的基本概念。在这篇博文,主要基于线阵介绍一些权值对波束的影响,这些加权的主要目的就是降低旁瓣,并使主波束的宽度增长最小。
均匀加权
均匀加权下的权值为
\[w_n=\frac{1}{N},n=0,\cdots,N-1 \]
此时可以得到\(u\)空间下的波束方向图为
\[B_u(u)=\frac{1}{N}\frac{sin(\frac{\pi Nd}{\lambda}u)}{sin(\frac{\pi d}{\lambda}u)} \]
cosine加权
考虑到N是奇数的情况下,cosine加权的权重系数可以表示成
\[w_{n}=sin(\frac{\pi}{2N})cos(\pi\frac{n}{N}) \]
将\(cos\)表示成指数函数形式并进一步化简得到波束方向图为
\[B(u)=\frac{1}{2}sin(\frac{\pi}{2N})\{ \frac{sin(\frac{N\pi}{2}(u-\frac{1}{N}))}{sin(\frac{\pi}{2}(u-\frac{1}{N}))}+\frac{sin(\frac{N\pi}{2}(u+\frac{1}{N}))}{sin(\frac{\pi}{2}(u+\frac{1}{N}))}{}\} \]
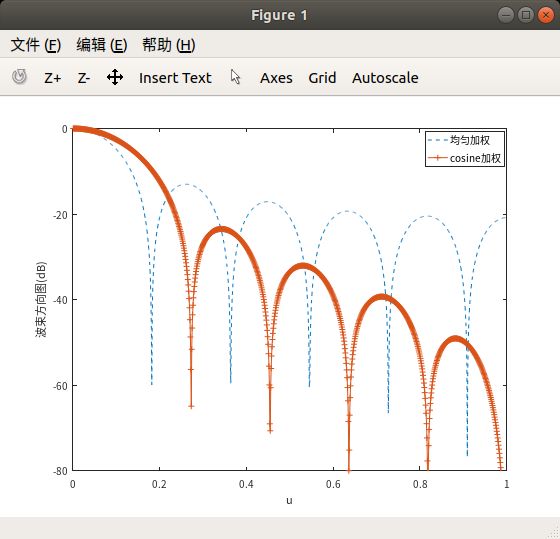
可以看到相较于均匀加权而言,`cosine`加权拥有更低的旁瓣,但是其主瓣波束宽度也增加了,相应的参数如下
| 权值 | 3dB带宽 |
第一零点 | 第一旁瓣高度 |
|---|---|---|---|
| 均匀加权 | \(0.89\frac{2}{N}\) | \(2\frac{2}{N}\) | -13dB |
| cosine加权 | \(1.18\frac{2}{N}\) | \(3\frac{2}{N}\) | -23.5dB |
升cosine加权
将矩阵加权和cosine加权结合起来,可以另外一种加权系数定义方法
\[w_n=c(p)(p+(1-p)cos(\pi\frac{n}{N})) \]
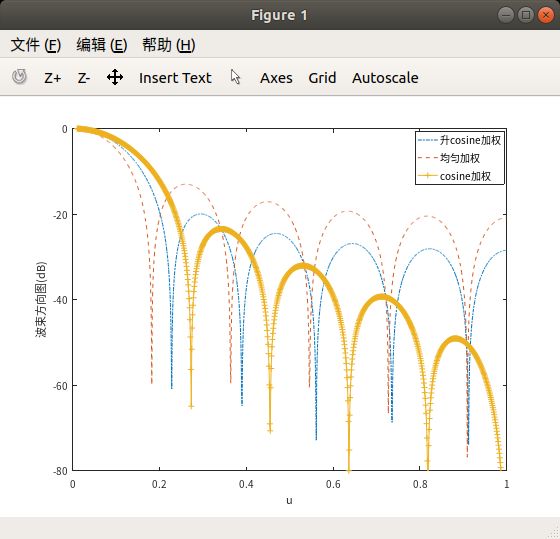
其中\(c(p)=\frac{p}{N}+\frac{1-p}{2}sin(\frac{\pi}{2N})\)是一个常数。设置\(p=0.31\),得到波束方向图如下
可以看到相对于前两种加权方式而言,升cosine加权有着更低的旁瓣,并且主波束宽度要小于cosine加权
Hamming加权
Hamming加权利用了矩形方向图和cosine平方方向图的特点,在第一旁瓣的峰值上放置了一个零点,此时加权函数为
\[w(n)=g_0+g_1cos(\frac{2\pi n}{N}) \]
其中\(g_0\)和\(g_1\)的选择使得在\(u=\frac{3}{N}\)的位置上有一个零点。对\(w(n)\)进一步化简可以得到
\[w(n)=0.54+0.46*cos(\frac{2\pi n}{N}) \]
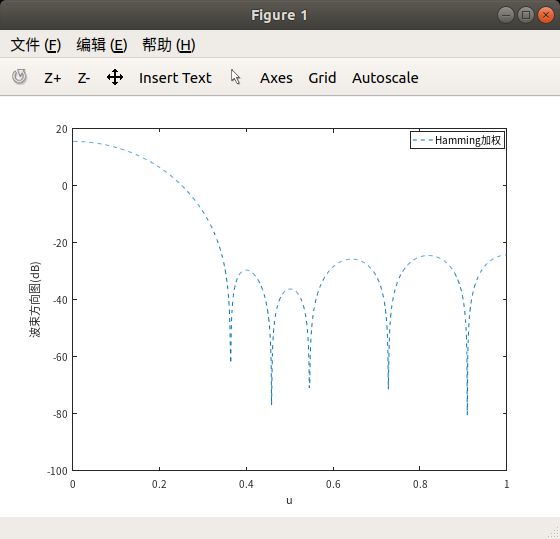
进而可以得到波束方向图
\[B(u)=0.54\frac{sin(\frac{N\pi u}{2})}{sin(\frac{\pi u}{2})}+0.23[\frac{sin(\frac{N\pi}{2})(u-\frac{2}{N})}{sin(\frac{\pi}{2})(u-\frac{2}{N})}+\frac{sin(\frac{N\pi}{2})(u+\frac{2}{N})}{sin(\frac{\pi}{2})(u+\frac{2}{N})}] \]
其加权波束方向图可以表示成
Kaiser加权
Kaiser加权的加权系数可以表示成
\[w(n)=I_{0}(\beta\sqrt{1-[\frac{2n}{N}]^2} \]
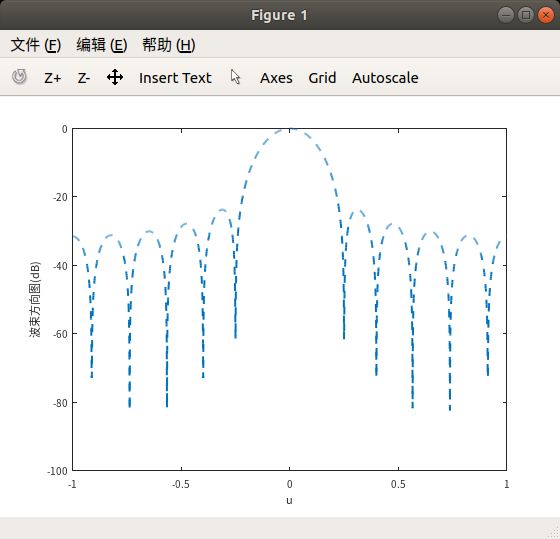
其中\(I_0(x)\)是零阶修正Bessel函数,参数\(\beta\)决定了波束方向图在旁瓣峰值高度和主波束宽度之间的性能折中情况。其波束方向图仿真如下
上面主要介绍了几种不同的加权方式对波束方向图的影响,还有许多其它的加权系数设计方案,包括长球函数,blackmanHaris加权等等。
相应的代码如下:
clear all
close all
M = 11;
d=0.5;
D = [-(M-1)/2:1:(M-1)/2]*d;
u = [0.001:0.001:1];
for i = 1 : length(u)
B(i) = (1 / M) * (sin(pi * M * d * u(i)) / sin(pi * d * u(i)));
B_cos(i) = 1/2 * sin(pi / (2*M)) * ( sin((M * pi / 2)*(u(i) - 1 / M))/(sin(pi *(u(i) - 1/M)/ 2)) + ...
sin((M * pi / 2)*(u(i) + 1 / M))/(sin(pi *(u(i) + 1/M)/ 2)));
end
figure(1)
plot(u,20*log10(abs(B)),'--', u, 20 * log10(abs(B_cos)), '-+');
ylabel('波束方向图(dB)');
xlabel('u');
legend('均匀加权','cosine加权')
axis([0 1 -80 0]);
clear all
close all
M=11;
d=0.5; % sensor spacing wrt wavelength
D = [-(M-1)/2:1:(M-1)/2]*d;
p = 0.31;
W_rcos = p*ones(1,M)+(1-p)*cos(pi*D*2/M);
u = [0.01:0.001:1];
for i = 1 : length(u)
B(i) = (1 / M) * (sin(pi * M * d * u(i)) / sin(pi * d * u(i)));
B_cos(i) = 1/2 * sin(pi / (2*M)) * ( sin((M * pi / 2)*(u(i) - 1 / M))/(sin(pi *(u(i) - 1/M)/ 2)) + ...
sin((M * pi / 2)*(u(i) + 1 / M))/(sin(pi *(u(i) + 1/M)/ 2)));
end
% Beampatterns
%c=p/M+(1-p)*2*sin(pi/(2*M));
A = exp(-j*2*pi*D.'*u);
G_rcos = W_rcos*A;
G_rcos = G_rcos/(max(abs(G_rcos)));
figure
plot(u,20*log10(abs(G_rcos)),'-.', u,20*log10(abs(B)),'--', u, 20 * log10(abs(B_cos)), '-+');
ylabel('波束方向图(dB)');
xlabel('u');
legend('升cosine加权','均匀加权','cosine加权')
axis([0 1 -80 0]);
close all
clear all
M = 11;
d = 0.5;
D = [-(M-1)/2:1:(M-1)/2]*d;
u = [0.001:0.001:1];
for i = 1 : length(u)
B(i) = 0.54 * sin(M * pi * u(i)/2)/sin(pi * u(i)/2) + 0.23 * ( sin((M * pi / 2)*(u(i)-2/M))/sin((pi/2)*(u(i)-2/M)) +...
sin((M * pi / 2)*(u(i)+2/M))/sin((pi/2)*(u(i)+2/M)));
end
figure(1)
plot(u, 20 * log10(abs(B)), '--')
xlabel('u')
ylabel('波束方向图(dB)')
legend('Hamming加权')
clear all
close all
N = 11;
beta = 3;
bes = besseli(0,beta);
for n = -(N-1)/2:(N-1)/2
x = 1-(2*n/N)^2;
wn1(n+1+(N-1)/2) = besseli(0,beta*sqrt(x));
end
wn1 = wn1'/bes;
u=(-1:0.001:1);
amf1=[-(N-1)/2:(N-1)/2]';
Vo1=exp(i*amf1*pi*u);
wn1=wn1/sum(wn1);
Beam1=20*log10(abs(wn1'*Vo1));
plot(u,Beam1,'--','Linewidth',2)
xlabel('u')
ylabel('波束方向图(dB)')
%axis([-1 1 -50 0])